| Элемент | Обозначение стержня | Усилия от единичных нагрузок, кН | Усилия от пост. нагрузки Р=51.62кН | Усилия от снеговой нагрузки Pс=32.40кН | Усилия от опорных моментов, к*Нм | Расчетные усилия, кН | ||||||
| P=1 | Млев= -1 | Мпр= -1 | nс=1 | nс=0,9 | Млев= -727,88 | Мпр= -221,21 | Σ | № загружений | +Раст., -Сжатие | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ВП | В-1 | 0 | 0.32 | 0 | 0.00 | 0.00 | 0.00 | 245.07 | 0.00 | 245.07 | 6,8,11 | 245.07 |
| Г-3,Д-4 | -5.48 | 0.25 | 0.08 | -282.88 | -177.55 | -159.80 | 191.46 | 20.73 | 212.20 | 6,7 | -460.43 | |
| Е-6 | -7.38 | 0.16 | 0.16 | -380.96 | -239.11 | -215.20 | 122.54 | 41.47 | 164.00 | 6,7 | -620.07 | |
| НП | А-2 | 3.08 | -0.29 | -0.04 | 158.99 | 99.79 | 89.81 | -222.10 | -10.37 | -232.46 | 6,7 | 258.78 |
| А-5 | 6.93 | -0.21 | -0.12 | 357.73 | 224.53 | 202.08 | -160.83 | -31.10 | -191.93 | 6,7 | 582.26 | |
| Раскосы | 1-2 | -4.65 | -0.06 | 0.06 | -240.03 | -150.66 | -135.59 | -45.95 | 15.55 | -30.40 | 6,8,11 | -406.03 |
| 2-3 | 3.45 | 0.06 | -0.05 | 178.09 | 111.78 | 100.60 | 45.95 | -12.96 | 32.99 | 6,8,11 | 311.68 | |
| 4-5 | -2.09 | -0.06 | 0.06 | -107.89 | -67.72 | -60.94 | -45.95 | 15.55 | -30.40 | 6,8,11 | -199.23 | |
| 5-6 | 0.68 | 0.06 | -0.06 | 35.10 | 22.03 | 19.83 | 45.95 | -15.55 | 30.40 | 6,8,11 | 85.33 | |
| Стойки | 3-4 | -1.00 | 0 | 0 | -51.62 | -32.40 | -29.16 | 0.00 | 0.00 | 0.00 | 6,7 | -84.02 |
| 6-7 | -1.00 | 0 | 0 | -51.62 | -32.40 | -29.16 | 0.00 | 0.00 | 0.00 | 6,7 | -84.02 | |
а) Условие прочности центрально-растянутого элемента:
σ=N/An≤Ry*gс,
где: N – расчетное усилие в рассматриваемом стержне;
Ry – расчетное сопротивление материала;
Аn – площадь сечения стержня нетто;
gс – коэффициент условий работы, gс=1 (для растянутых элементов).
Требуемая площадь центрально-растянутого элемента из условия прочности:
Anтр≥N/Ry
Далее подбираем равнополочные уголки по ГОСТ 8509-93.
б) Условие устойчивости центрально-сжатого стержня:
σ=N/(φ*A)≤Ry*gс,
где: А – площадь сечения элементов брутто;
j – коэффициент продольного изгиба, который зависит от гибкости стержня l.
Коэффициент условия работы учитывают для тех стержней решетки, которые получаются с небольшим сечением гибкостью l ³ 60 и которые могут легко деформироваться во время изготовления, транспортирования и монтажа фермы. Следовательно, для сжатых раскосов (кроме опорного) и стоек при l ³ 60 gс=0,8.
Требуемая площадь центрально-сжатого стержня из условия устойчивости:
Aтр≥N/(φ*gс*Ry)
т.к. коэффициент j в неявном виде зависит от площади сечения, то задачу решают методом последовательных приближений. В первом приближении задаемся: для поясов l=80…100, для раскосов и стоек l=100…120.
Определив j в зависимости от l и Ry вычисляем величину Атр в первом приближении, из сортамента подбираем соответствующие профили уголков.
Необходима проверка принятого сечения по условию устойчивости: сжатый стержень потеряет устойчивость в той плоскости, относительно которой гибкость максимальная, т.к. при этом j минимальный. Поэтому вычисляем гибкости lx и ly:
lx=lefx/rx,
ly=lefу/rx,
где lefx – расчетная длина сжатого стержня в плоскости фермы;
lefу – то же, из плоскости фермы;
rx, ry – радиусы инерции сечения относительно осей х и у.
Для верхнего пояса расчетная длина стержня:
lefx=l,
где l – расстояние между центрами узлов.
Расчетная длина опорного раскоса:
lefx=0,5*l.
Для остальных сжатых стержней раскосов и стоек вводится коэффициент опорного защемления m=0.8, так что расчетная длина будет:
lefx=0,8*l,
Для определения расчетных длин сжатых стержней из плоскости фермы рассматривается схема связей по верхним поясам ферм.
Связи по верхним поясам ферм уменьшают расстояние между узлами, закрепленными от горизонтального смещения, поэтому:
lefу=lзакр,
где lзакр – расстояние между закрепленными от горизонтального смещения точками (при беспрогонной системе покрытия lзакр равно шагу узлов фермы верхнего пояса).
Для сжатых раскосов и стоек расчетная длина при расчете устойчивости из плоскости фермы принимается по формуле lefx=l.
Слабозагруженные сжатые стержни решетки рассчитываются по предельной гибкости, а сечения подбирают по требуемому радиусу инерции:
rminтр=lefу/lпр.
Предельная гибкость:
- для сжатых стержней поясов и опорных раскосов: lпр=180-60*α;
- для сжатых стержней раскосов и стоек: lпр=210-60*α;
- для растянутых стержней: lпр=400,
где α=N/(φmin*A*Ry*gс)≥0.5.
Толщину фасонок назначаем конструктивно, исходя из величины усилий в опорном раскосе: при N=-406.05принимаем толщину фасонки tф=12 мм.
Во избежание повреждения при транспортировке и монтаже наименьший уголок принимается с размерами 50х5 мм.
Все расчеты сведены в таблицу 5.
Таблица 5
Таблица подбора сечений стержней ферм
(толщина фасонки t ф= 12 мм, уклон i = 0 , сталь С245 , Ry= 240 МПа)
| Элемент | Обозначение стержня | Расчетное усилие | Сечение, мм | Площадь сечения, см2 | Геометрическая длина, мм | Расчетная длина, см | Радиусы инерции, см | Гибкости | Предельная гибкость | Коэф. продольного изгиба | Коэф. условий работы | Расчетное напряжение, МПа | Недонапряжение, % | |||||
| - | - | N | b | t | А | l | lxеf | lуеf | rx | ry | lx | ly | lпр | jmin | gc | σ | ∆ | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| ВП | В-1 | 245.07 | 125 | 9 | 43.9 | 2800 | 280 | 280.0 | 3.81 | 5.63 | 73.4 | 49.7 | 400 | - | 0.95 | 55.9 | 308.2 | |
| Г-3, Д-4 | -460.43 | 125 | 9 | 43.9 | 3000 | 300 | 300 | 3.81 | 5.63 | 78.7 | 53.3 | 140 | 0.696 | 0.95 | -150.8 | 51.2 | ||
| Е-6 | -620.07 | 125 | 9 | 43.9 | 3000 | 300 | 300 | 3.81 | 5.63 | 78.7 | 53.3 | 127 | 0.696 | 0.95 | -203.1 | 12.2 | ||
| НП | А-2 | 258.78 | 100 | 7 | 27.3 | 5800 | 580 | 580 | 3.05 | 4.56 | 190.2 | 127.2 | 400 | - | 0.95 | 94.8 | 140.5 | |
| А-5 | 582.26 | 100 | 7 | 27.3 | 6000 | 600 | 600 | 3.05 | 4.56 | 196.7 | 131.6 | 400 | - | 0.95 | 213.3 | 6.9 | ||
| Раскосы | 1-2 | -406.03 | 110 | 8 | 34.3 | 4220 | 211 | 422 | 3.36 | 4.99 | 62.9 | 84.6 | 123 | 0.651 | 0.8 | -181.7 | 5.6 | |
| 2-3 | 311.68 | 63 | 6 | 14.7 | 4250 | 425 | 425 | 1.92 | 2.97 | 221.2 | 143.2 | 400 | - | 0.95 | 211.4 | 7.8 | ||
| 4-5 | -199.23 | 100 | 7 | 27.3 | 4360 | 348.8 | 436 | 3.05 | 4.56 | 114.4 | 95.7 | 160 | 0.452 | 0.8 | -161.6 | 18.8 | ||
| 5-6 | 85.33 | 50 | 5 | 9.8 | 4250 | 425 | 425 | 1.53 | 2.41 | 278.7 | 176.5 | 400 | - | 0.95 | 87.5 | 160.5 | ||
| Стойки | 3-4 | -84.02 | 63 | 6 | 14.7 | 3090 | 247.2 | 309 | 1.92 | 2.97 | 128.6 | 104.1 | 162 | 0.371 | 0.8 | -153.4 | 25.1 | |
| 6-7 | -84.02 | 63 | 6 | 14.7 | 3090 | 247.2 | 309 | 2.97 | 2.97 | 83.3 | 104.1 | 175 | 0.515 | 0.8 | -110.6 | 73.6 | ||
Для ферм пролетом 24 м оптимальное количество типоразмеров - 4…5, и сечения поясов не меняют, поэтому окончательно принимаем:
В-1, Г-3, Д-4, Е-6 – ∟125х9;
1-2 – ∟110х8;
А-2, А-5, 4-5 – ∟100х7;
2-3, 3-4, 6-7 – ∟63х6;
А-1, 5-6 – ∟50х5.
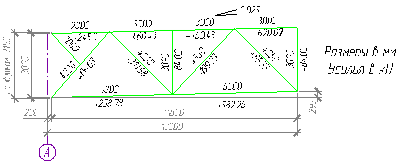
Рисунок 14. Геометрическая схема полуфермы
Дата: 2019-07-31, просмотров: 368.