Экономико-математическая модель это система формализованных соотношений, описывающих основные взаимосвязи элементов, образующих экономическую систему. Система экономико-математических моделей эконометрического типа служит для описания относительно сложных процессов экономического или социального характера.

Определенные виды моделей экономического и социального прогнозирования могут классифицироваться в зависимости от критерия оптимизации или наилучшего ожидаемого результата.

С учетом фактора времени модели могут быть статическими, когда ограничения в модели установлены для определенного отрезка времени, или динамическими – в этом случае ограничения установлены для нескольких отрезков времени.

Различают факторные и структурные модели экономического типа. Один и тот же тип моделей может быть применим к различным экономическим объектам. В зависимости от уровня рассмотрения показателей народного хозяйства различают макроэкономические, межотраслевые, отраслевые и региональные модели.

Факторные модели описывают зависимость уровня и динамики того или иного показателя от уровня и динамики влияющих на него экономических показателей – аргументов или факторов. Факторные модели могут включать различное количество переменных величин и соответствующих им параметров. Простейшими видами факторных моделей являются однофакторные, в которых фактором является какой-либо временный параметр. Многофакторные модели позволяют одновременно учитывать воздействие нескольких факторов на уровень и динамику прогнозируемого показателя.

Обоснованность прогноза в значительной мере зависит от выбора метода прогнозирования. Практическое применение того или иного метода прогнозирования определяется такими факторами, как объект прогноза, сложность и структура системы, наличие исходной информации, квалификация прогнозиста.

Экстраполяционные методы являются одним из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования. В общем случае для экстраполяции необходимо иметь временной ряд, где каждому значению независимой переменной (в качестве которой выступает время) соответствует определенное значение прогнозируемою показателя. При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта.

Следует отметить, что, поскольку метод разработан для анализа временных рядов, состоящих из большого числа наблюдений, а временные ряды в отраслевом прогнозировании, как правило, невелики, прогноз, сделан­ный с помощью этого метода, может не отразить некоторых существенных изменений.

Прогнозную экстраполяцию можно разбить на два этапа.

Выбор оптимального вида функции, описывающей ретроспективный ряд данных. Выбору математической функции для описания тренда предшествует преобразование исходных данных с использованием сглаживания и аналитического выравнивания динамического ряда. Расчет коэффициентов функции, выбранной для экстраполяции.

При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого временного ряда, на которую уже накладываются другие составляющие. Результат при этом связывается исключительно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов. В статистической литературе под тенденцией развития понимают некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.

Для оценки коэффициентов чаще остальных используется метод наименьших квадратов (МНК). Его сущность состоит в минимизации суммы квадратических отклонений между наблюдаемыми величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.

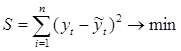 (1.1)

где 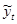 – расчетные значения тренда;

y – фактические значения ретроспективного ряда;

n – число наблюдений.

Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неучтенных.

Операцию экстраполяции в общем виде можно представить в виде определения значения функции

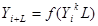 (1.2)
где 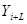 - экстраполируемое значение уровня;

L – период упреждения;

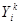- уровень, принятый за базу экстраполяции.

Экстраполяция на основе средней.

В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции и к изменению или если это изменение незначительно, можно принять 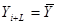 т. е. прогнозируемый уровень равен среднему значению уровней в прошлом. Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:   

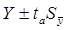 (1.3)
где t_a – табличное значение t-статистики Стьюдента с n-1 степенями свободы и уровнем вероятности p;

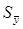 – средняя квадратическая ошибка средней.

Значение ее определяется по формуле 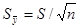. В свою очередь, среднее квадратическое отклонение S для выборки равно

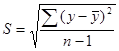 (1.4)

Доверительный интервал, полученный как 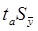, учитывает неопре­деленность, которая связана с оценкой средней величины. Общая дисперсия составит величину 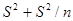. Таким образом, доверительные интервалы для прогностической оценки равны

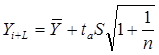(1.5)

Недостаток рассмотренного подхода заключается в том, что доверительный интервал не связан с периодом упреждения.

Экстраполяция по скользящей и экспоненциальной средней.

Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие средние. Если прогнозирование ведется на один шаг вперед, то 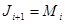 или 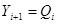, где М_i - адаптивная скользящая средняя; Q_i - экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить аналогично тому, как это было сделано в формуле (1.5), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m. Так как m обычно берется равной нечетным числам, то подсчи­таем для них соответствующие значения величины 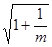. Что касается экспоненциального сглаживания, то, так как дисперсия экспо­ненциальной средней равна 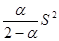, где S₂ - среднее квадратическое отклонение, вместо величины  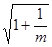в формуле, приведенной выше, при исчислении доверительного интервала прогноза следует взять величину  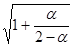или 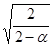. Здесь  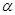— коэффициент экспоненциального сглаживания.

Корреляционный анализ используют для выявления и оценки связи между различными показателями. Степень тесноты связи оценивают коэффициентами, изменяющимися в пределах от 0 до 1, по следующей формуле:

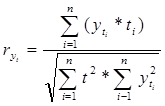(1.6)

Малое значение коэффициента свидетельствует о слабой связи, значение, близкое к 1, характеризует очень сильную связь и часто позволяет предположить наличие функциональной причинно-следственной связи. Затем проверяют значимость коэффициента корреляции по критерию Стьюдента t_j,k:

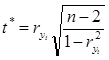 (1.7)
где k=n-2 – число степеней свободы.

При выполнении неравенства t*>y_j,k гипотеза о не значимости коэффициента парной корреляции отвергается, т.е. y_t зависит от фактора времени. Затем выбирают математическую модель взаимосвязи показателя от времени и рассчитывают критерии точности полученной модели.

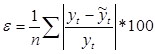 (1.8)

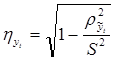 (1.9)

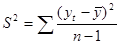 (1.10)
где 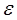– средняя относительная ошибка;

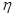 – корреляционные отношения;

S₂ – остаточная дисперсия;

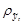– среднеквадратическое отклонение, рассчитанное по формуле:

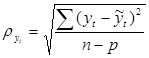 (1.11)
где p- количество расчетных коэффициентов уравнения тренда.

Затем делают расчет точечной и интервальной оценки прогноза:

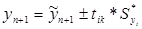 (1.12)

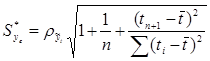 (1.13)
где y_n+1 – прогнозируемая величина.

С помощью этих методов экстраполируются количественные пара­метры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результативности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др .

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20—25 лет. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую перспек­тиву прогнозирования тех или иных объектов — на 5—7 лет.

При экстраполяции часто используются линейные модели. Они требуют относительно небольшого количества вычислений и по тому, в частности, широко распространены в прак­тике прогнозирования. Их недостаток, заключающийся в том, что лишь немногие явления в экономике могут быть адекватно описаны в линейном виде, отчасти преодолевается с помощью кусочно-линейной аппроксимации.

ДУБЛИРУЮЩИЕ ПОРТФЕЛИ