интервал 0 £ j £ a
M1(j) = M(j)/(PRтр.н) = [1/(2sina)]{(1/p)[(0,5a +
+ asin2a + 1,5sinaсosa] – 0,5sin2a – 0,5sin2j};
интервал a £ j £ p – a
M1(j) = M(j)/(PRтр.н/2sina) = [1/(2sina)]{(1/p)[(0,5a +
+ asin2a + 1,5sinaсosa] – 0,5sin2a – sinasinj + 0,5sin2a}.
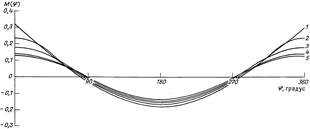
Графики, иллюстрирующие изменение изгибающего момента, приведены на рис. 13, 14. Из них следует, что оптимальным с точки зрения минимизации напряжений, возникающих при сжатии плашкой трубы и действии распределенной нагрузки, является значение угла охвата a, близкое к 90°. Достигнуть такой величины по конструктивным соображениям невозможно, поэтому в качестве максимального значения следует принимать a = 80 ¸ 85°.
Это же положение относится и к случаю действия двух пар сосредоточенных сил. Однако этот вариант нагружения является промежуточным при переходе к распределенной нагрузке.
При условии равенства геометрических размеров поперечных сечений гибких труб для трех рассмотренных вариантов взаимодействия их с плашками наиболее опасным будет случай, при котором возникает максимальный по модулю изгибающий момент. При проведении прочностных расчетов следует, в первую очередь, учитывать растягивающие напряжения, которые суммируются с растягивающими напряжениями, возникающими при действии давления технологической жидкости.
Максимальные значения изгибающих моментов для трех рассмотренных случаев представлены ниже:
| Способ приложения нагрузки ......................................... | Две сосредоточенные силы | Две пары сосредото- ченных сил | Распределенная нагрузка |
| Максимальный изгибающий момент ............................................ | 0,318PRтр.н | 0,24PRтр.н | 0,125PRтр.н |
| Координата сечения трубы j, в которой действует максимальный момент, градус .... | 0 | 0 | 0 и 90 |
|
| Рис. 13. Эпюра изгибающих моментов М(j) в поперечном сечении гибкой трубы, взаимодействующей с плашками при Rтр.н < Rп: 1 – сосредоточенная сила; угол охвата трубы плашкой a, градус: 2 – 20, 3 – 40, 4 – 60, 5 – 80; j – текущая координата |
|
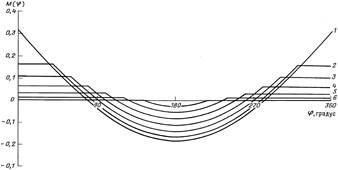
| Рис. 14. Эпюра изгибающих моментов М(j) в поперечном сечении гибкой трубы, взаимодействующей с плашками при Rтр.н > Rп: 1 – сосредоточенная сила; угловая координата точек приложения сил a, градус: 2 – 20, 3 – 30, 4 – 40, 5 – 60, 6 – 80; j – текущая координата |
Из приведенных данных следует, что наиболее предпочтительным случаем при взаимодействии трубы и плашек является приложение распределенной нагрузки. Вместе с тем, при действии двух сосредоточенных сил деформация поперечного сечения трубы приводит к увеличению площади контакта и в итоге к передаче усилия по всей площади плашки. Картина деформации поперечного сечения при приложении двух пар сосредоточенных сил является более сложной. При угле a 40 ¸ 50° они могут вызвать сплющивание трубы. Но поскольку подобные значения углов в плашках не предусмотрены, данный вопрос как представляющий сугубо теоретический интерес рассмотрен не будет.
Исходя из полученных зависимостей ,может быть вычислен изгибающий момент и определены максимальные напряжения, возникающие при обжатии трубы плашками.
Рассмотрим пример расчета напряжений в предположении, что отсутствует давление технологической жидкости во внутренней полости трубы и на нее нет осевой нагрузки.
Под действием изгибающего момента в продольном сечении гибкой трубы возникают нормальные напряжения, максимальное значение которых определяется следующим образом:
sx = Mx1/Wx1,
где Mx1 = KнагрP1R – максимальное значение изгибающего момента, действующего в поперечном сечении, в расчете на единицу длины трубы (значения максимальных моментов и соответствующих коэффициентов нагружения Kнагр приведены выше); Wx1 = bтрd2тр/6 – момент сопротивления изгибу поперечного сечения трубы, имеющей длину, равную единице (где dтр – толщина стенки трубы; bтр – ширина ее поперечного сечения, в рассматриваемом случае b = 1).
Моменты сопротивления изгибу для труб различной толщины имеют следующие значения:
| Толщина стенки трубы, dтр, мм ....................... | 2 | 2,5 | 3 | 3,5 | 4 | 5 |
| Момент сопротивления изгибу, мм3 ............ | 0,667 | 1,667 | 1,500 | 2,040 | 2,667 | 4,167 |
Максимальное усилие, приложенное к единице длины трубы, ограничено и определяется максимально допустимыми нормальными напряжениями, возникающими при изгибе за пределом упругости при образовании пластического шарнира. При расчете деталей транспортера и режимов его работы максимальное сжимающее усилие может быть установлено из условия равенства этих напряжений пределу текучести:
sx = sт = Mx1/Wx1 = KнагрP1R/Wx1.
Отсюда величина сжимающей силы P1, особенности приложения которой к трубе характеризует коэффициент Kнагр, может быть найдена из выражения
P1 = Wx1sт/KнагрR.
Значения максимальной нагрузки для наиболее распространенных размеров труб приведены ниже:
| Параметры трубы, мм: | ||||||
| наружный диаметр dтр.н | 25 | 25 | 33 | 33 | 44 | 44 |
| толщина стенки dтр .......... | 2 | 2 | 3 | 3 | 3,5 | 3,5 |
| Предел текучести sт, МПа | 480 | 700 | 480 | 700 | 480 | 700 |
| Максимальная сжимающая сила Р1, Н/мм: | ||||||
| сосредоточенная ............... | 87,5 | 127,5 | 151 | 220,2 | 153,9 | 224,4 |
| распределенная ................. | 222,7 | 324 | 383,4 | 559,2 | 390 | 570 |
| Примечание. Предел текучести 480 МПа соответствует малоуглеродистым сталям, а 700 МПа – низколегированным. | ||||||
Приведенные значения максимальной сжимающей силы P1 служат исходными данными при определении максимального тягового усилия инжектора.
Дата: 2019-07-31, просмотров: 326.