Глобальные навигационные спутниковые системы.

В настоящее время для определения положения точек или объектов в пространстве широко применяются глобальные навигационные спутниковые системы (ГНСС): американская NAVSTAR GPS (Navigation Satellite Timing and Ranging Global Positioning System) и российская ГЛОНАСС (Глобальная Навигационная Спутниковая Система). Их глобальность обеспечивается функционированием на околоземных орбитах искусственных спутников (ИСЗ), видимых из любой точки Земли. Данные спутники непрерывно передают высокоточные измерительные сигналы и создают, таким образом, вокруг нашей планеты информационное координатно-временное поле. Используя данное поле, с помощью специального приемника и программного обеспечения можно определять положение точек и объектов в пространстве и времени.

Принцип действия ГНСС

Принцип, на котором основано действие ГНСС, весьма прост – местоположение объекта определяется путем измерения расстояний от него до исходных точек, координаты которых известны. Сложность его реализации с помощью ГНСС обусловлена стремлением сделать систему глобальной, т. е. доступной в любое время на всей Земле и в окружающем пространстве. Для этого в качестве исходных точек выбраны искусственные спутники Земли, излучающие дальномерные радиосигналы, которые пользователь принимает на специальный приемник. Так как спутники движутся по своим орбитам, система предоставляет пользователю информацию о координатах ИСЗ на любой момент выполнения измерений.

Применяемый в ГНСС метод определения местоположения точек основан на линейной геодезической засечке. Ее суть сводится к известной геометрической задаче: найти на плоскости положение точки K, если известны положения двух других точек А и В и расстояния от них до точки K соответственно S1 и S2 (рис. 102).

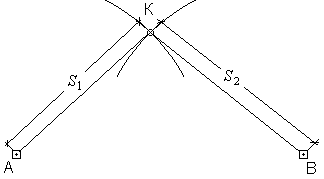
Рис. 102. Линейная засечка

Применяемый в ГНСС метод определения местоположения точек основан на линейной геодезической засечке. Ее суть сводится к известной геометрической задаче: найти на плоскости положение точки K, если известны положения двух других точек А и В и расстояния от них до точки K соответственно S₁ и S₂ (рис. 102).

Искомая точка K принадлежит одновременно двум окружностям с радиусами S₁ и S₂, описанным из центров А и В, т. е. является одной из двух точек пересечения этих окружностей. В аналитическом представлении эта задача выражается в виде системы двух уравнений

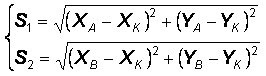
где XА, YА, XВ, YВ и XK, YK – прямоугольные координаты точек на плоскости. Таким образом, искомые координаты XK, YK точки K получаются из решения системы двух уравнений с двумя неизвестными. При обобщении этой задачи от плоского построения к пространственному вводится третья координата Z, и для определения теперь уже трех искомых координат ХK, YK, ZK точки K необходимо решить систему из трех уравнений

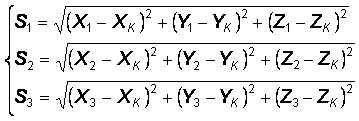
Следовательно, при решении пространственной линейной засечки должно быть три исходных пункта, которые не должны лежать на одной прямой, иначе система уравнений не будет иметь определенного решения. Количество исходных точек, до которых измеряются расстояния, может быть и больше трех, тогда система уравнений становится переопределенной, и задача решается методом наименьших квадратов. Привлечение избыточных измерений, позволяет повысить точность определения координат и к тому же дает еще возможность включения в систему уравнений дополнительных неизвестных параметров, определение которых необходимо для корректной работы с ГНСС.

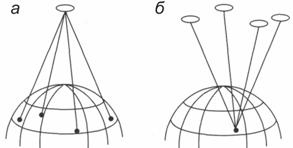
Рис. 103. Схемы определения координат спутника (а) и наземного пункта (б) ;

С помощью описанного метода линейной геодезической засечки в ГНСС решаются две главные задачи (рис. 103): - определение координат спутника по измеренным до него расстояниям от наземных пунктов с известными координатами (прямая геодезическая засечка); - определение координат наземного (или надземного) объекта по измеренным до него расстояниям от нескольких спутников, координаты которых известны (обратная геодезическая засечка).