ЗАДАЧА 1 Имеются следующие данные
Таблица 1 - Производство продукции предприятия (в сопоставимых ценах), млн. руб.
| Год | 2014 | 2015 | 2016 |
| Объем продукции | 117 | 122 | 128 |
Определить аналитические показатели ряда динамики производства продукции предприятия за 2014 -2016 гг.:
1) абсолютные приросты (цепные и базисные);
2) темпы роста (цепные и базисные);
3) темпы прироста (цепные и базисные);
4) абсолютные значения одного процента прироста;
5) средний абсолютный прирост за 2014 -2016 гг.;
6) средний темп роста за 2014 -2016 гг. и среднегодовой темп прироста;
7) среднегодовое производство продукции.
Решение:
1) Определим абсолютные приросты:
цепные базисные
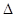 yц = уi – yi -1
yц = уi – yi -1 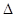 yб = уi – yо
yб = уi – yо
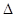 y15=122–117=5 млн. руб.
y15=122–117=5 млн. руб. 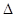 y15=122–117= 5 млн. руб.
y15=122–117= 5 млн. руб.
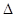 y16=128–122=6 млн. руб.
y16=128–122=6 млн. руб. 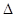 y16=128–117= 11 млн. руб.
y16=128–117= 11 млн. руб.
2) Определим темпы роста:
цепные базисные
k = 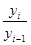 k =
k = 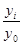
k15= 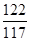 =1,043 k15=
=1,043 k15= 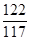 =1,043
=1,043
k16= 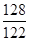 =1,049 k16=
=1,049 k16= 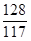 =1,094
=1,094
3) Определим темпы прироста:
цепные базисные
Δkц = kц *100% – 100% Δkб = kб *100% – 100%
Δk15=104,3–100=4,3 % Δk15=104,3–100=4,3 %
Δk16=104,9–100=4,9 % Δk16=109,4–100=9,4 %
4) Определим абсолютное значение одного процента прироста:
А % = 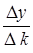 или А % = 0,01 у i -1
или А % = 0,01 у i -1
А %15= 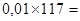 1,17 млн. руб.
1,17 млн. руб.
А %16= 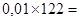 1,22 млн. руб.
1,22 млн. руб.
Все перечисленные показатели динамики оформляем в итоговую таблицу.
Таблица 2 - Показатели динамики производства продукции предприятия за 2014 -2016 гг.
| Год | Произв-во продукции, млн. руб. | Абсолютные приросты, млн. руб. | Темпы роста, % | Темпы прироста, % | Абсолют. значение 1% прироста, тыс. руб. | |||
| цепные (ежегод.) | базисные (к 2014г.) | цепные (ежегод.) | базисные (к 2014г.) | цепные (ежегод.) | базисные (к 2014г.) | |||
| 1 | 2 | 3 | 4 | 4 | 6 | 7 | 8 | 9 |
| 2014 2015 2016 | 117 122 128 | - 5 6 | - 5 11 | - 104,3 104,9 | - 104,3 109,4 | - 4,3 4,9 | - 4,3 9,4 | – 1,17 1,22 |
5) Средний абсолютный прирост определяется двумя способами:
а) как средняя арифметическая простая (через сумму цепных абсолютных приростов):
Δ 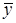 =
= 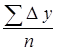 =
= 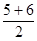 =5,5 млн. руб.,
=5,5 млн. руб.,
где n – число цепных абсолютных приростов;
б) как отношение базисного прироста к числу периодов:
Δ 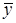 =
= 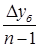 =
= 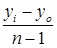 ,
,
где n – число периодов, включая базисный;
Δ 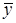 =
= 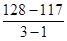 =
= 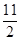 =5,5 млн. руб.
=5,5 млн. руб.
6) Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
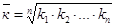 =
= 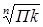 ,
,
где n – число цепных темпов роста;
П – знак произведения;
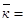
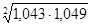 =1,046 или 104,6 %.
=1,046 или 104,6 %.
Согласно правилу взаимосвязи цепных и базисных темпов роста: произведение цепных темпов равно базисному темпу. Поэтому среднегодовой темп роста может быть исчислен из отношения конечного (уn) и базисного (yo) уровней по формуле:
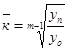 ,
,
где m – число периодов, включая базисный;
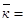
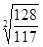 =1,046 или 104,6 %
=1,046 или 104,6 %
Среднегодовой темп роста за 2014 -2016 гг. равен 104,6 %.
Среднегодовой темп прироста исчисляется следующим образом:
Δ = % – 100%=104,6–100=4,6%.
Таким образом, производство продукции за период 2014 -2016 гг. увеличивалось за год в среднем на 4,6%.
7) В примере имеем интервальный ряд динамики с равными интервалами. Поэтому среднегодовое производство продукции исчислим по формуле средней арифметической простой:
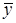 =
= 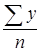 =
= 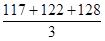 =122,3 млн. руб.,
=122,3 млн. руб.,
где у – уровни ряда
n – число уровней ряда.
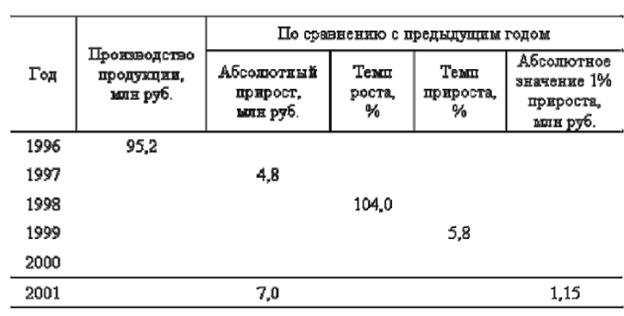
ЗАДАЧА 3 Используя взаимосвязь показателей, определите недостающие в таблице показатели динамики. Сделайте вывод.
|
Дата: 2019-07-30, просмотров: 462.