Таблица 1 - Нормы выработки работниками предприятия
| Группы работников по выполнению норм выработки, % | Число работников, чел |
| 80-90 90-100 100-110 110-120 120-130 130-140 | 3 7 22 48 16 4 |
| Итого | 100 |
Определить модальную и медианную нормы выработки.
Решение: Прежде всего, определяем модальный интервал. Наибольшей частоте соответствует модальный интервал. Наибольшее число работников 48 человек выполняют норму выработки в интервале 110-120 (%), который и является модальным интервалом:
Мо = 110+10 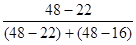 = 114,5 (%).
= 114,5 (%).
Большинство работников на предприятии выполняют норму выработки на 114,5%.
ЗАДАЧА 9 Медиана - варианта, которая находится в середине вариационного ряда, то есть делит ряд пополам.
! Медианным будет интервал, накопленная частота которого равна или превышает половину суммы частот ( 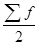 ). Комулятивная частота образуется путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака.
). Комулятивная частота образуется путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака.
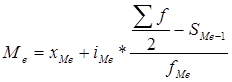
где 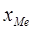 - начальное значение медианного интервала,
- начальное значение медианного интервала,
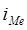 - величина медианного интервала,
- величина медианного интервала,
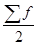 - полусумма частот,
- полусумма частот,
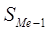 - сумма накопленных частот, предшествующих медианному интервалу,
- сумма накопленных частот, предшествующих медианному интервалу,
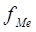 - частота медианного интервала.
- частота медианного интервала.
Таблица 1 - Нормы выработки работниками предприятия
| Группы работников по выполнению норм выработки, % | Число работников | Накопленные частоты |
| 80-90 90-100 100-110 110-120 120-130 130-140 | 3 7 22 48 16 4 | 3 3+7=10 3+7+22=32 32+48=80 96 100 |
| Итого | 100 | - |
Определить медиану.
Решение: Определяем медианный интервал. Для этого подсчитаем сумму частот – 100, половинка суммы (100:2) = 50, то есть комулятивная частота не должна быть ниже 50 (чел.).
Образуем комулятивную частоту, накапливая частоты от интервала 80-90 (3+7+22+48=80). Значит, медиальный интервал будет от 110 до 120, где находится медиана:
Ме = 110+10 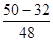 = 113,8 (%).
= 113,8 (%).
Из расчета видно, что половина работников выполняют норму выработки до 113,8%, а половина выше 113,8%. То есть норма выработки 113,8% делит ряд пополам.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
ЗАДАЧА 10 Среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений отдельных вариантов признаков от их средних.
Простое среднее линейное отклонение вычисляется в случае, когда каждый вариант повторяется один раз, т.е. для несгруппированных данных (первичного ряда):
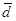 =
= 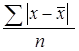
где х – индивидуальные значения признака (вариант);
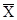 – среднее значение признака;
– среднее значение признака;
n – число признаков
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9лет. Определить: простое среднее линейное отклонение, если требумый опыт работы на должность составляет в среднем 5 лет.
В примере: 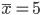 лет;
лет;
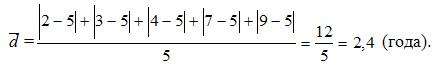
Ответ: 2,4 года.
ЗАДАЧА 11
Таблица 1 - Группировка вкладчиков по размеру вклада в банке города
| Размер вклада, руб. | До 4000 | 4000-6000 | 6000-8000 | 8000-10000 | Св. 10000 |
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определить средний размер вклада и среднее квадратическое отклонение, дисперсию, коэффициент вариации. Сделать выводы.
Решение: Для расчета среднего размера вклада и среднего квадратического отклонения строим расчетную таблицу 2.
Открытые интервалы – закрвают исходя из шага поседующего или предшествующего закрытого интервала.
Открытый интервал «до 4000» – исходя из шага интервала (6000-4000)=2000, т.е.закрываем интервал 2000-4000.
Открытый интервал «всыше 10000» – исходя из шага интервала (10000-8000)=2000, т.е.закрываем интервал 10000-12000.
Преобразуем интервальный ряд динамики в моментный (исходя из расчета средних величин).
Таблица 2 - Расчет среднего квадратического отклонения
| Группы вкладчиков по размеру вклада, руб. х | Число вкладчи-ков f | xf |
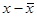
|
( 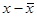 )2 )2
|
( 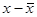 )2 f )2 f
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| (2000+4000)/2 =3000 5000 7000 9000 11000 | 32 56 120 104 88 | 96000 280000 840000 936000 968000 | 3000-7800= -4800 | (-4800)2=23040000 | 23040000*32=737280000 |
| Итого | 400 | 3120000 | – | – | 2304000000 |
Определим средний размер вклада:
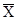 =
= 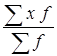 = 3120000/ 400= 7800 руб.
= 3120000/ 400= 7800 руб.
Определим среднее квадратическое отклонение – является абсолютной мерой вариации признака в совокупности и выражается в тех же единицах измерения варьирующего признака.
σ = 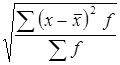 =
= 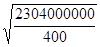 = 2400 руб.
= 2400 руб.
Дисперсия признака (σ2) Дисперсия - средняя арифметическая квадратов отклонений конкретных значений варьирующего признака от его средней арифметической.
Простая (общая) дисперсия
σ2 = 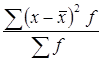 = 5760000
= 5760000
Дата: 2019-07-30, просмотров: 610.