ЗАДАЧА 1 Имеются следующие данные о товарообороте ИП «Солнышко»
|
| 4 квартал 2016 у0 | 4 квартал 2017 | Итого 2017год | |
| план упл | факт у1 | |||
| Товарооборот, тыс. руб. | 200 | 280 | 292,5 | 1570 |
| структура | - | |||
Товарооборот у ИП «Лукошко» за 2017г составил 1305 тыс. руб.
Определить:
1. относительную величину планового задания 4 кв. 2017г. по ср. с 4 кв. 2016г,
2. относительную величину выполнения плана в 4 кв. 2017г.,
3. относительную величина динамики 4 кв. 2017г. по сравнению с 4 кв. 2016г. – двумя способами (через взаимосвязь),
4. относительный показатель структуры 4 кв. 2017г. в итого 2017 г.,
5. относительную величину сравнения товарооборота за 2017г. ИП «Солнышко» и ИП «Лукошко».
ОВПЗ = 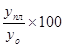 Решение: ОВПЗ =
Решение: ОВПЗ = 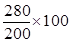 = 140%.
= 140%.
Таким образом, в 4 квартале 2017г. по ср. с 4 ув 2016г. планируется увеличение товарооборота магазина на 40%.
ОВВП = 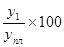 .
.
ОВВП = 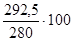 = 104,5%.
= 104,5%.
План по товарообороту магазина выполнен на 104,5%, т.е. перевыполнение плана составило 4,5%.
ОВД (Т) = 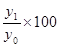 .
.
ОВД = 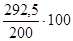 = 146,3%
= 146,3%
Товарооборот магазина увеличился в 4квартале 2017г по сравнению со 4 кв 2016 кварталом на 46,3%.
Взаимосвязь: 1, 463 = 1, 045 * 1, 4
d = 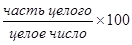 . dII =
. dII = 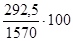 = 18,6% и т.д.
= 18,6% и т.д.
ОВС = 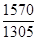 *100= 120,3%
*100= 120,3%
Следовательно, товарооборот 4 кв 2015 г у ИП Солнышко по сравнению с ИП Аленка меньше на 4%.
ЗАДАЧА 3 Относительная величина координации (ОВК) – характеризуют отношения частей изучаемой совокупности к одной из них, взятой за базу сравнения.
Имеются следующие данные о численности экономически активного населения страны по состоянию на начало года, млн. человек:
экономически активное население 71,2
в том числе:
занятые в экономике 64,9
безработные 6,3.
Рассчитать, сколько безработных приходится на 1000 занятых в экономике России.
Решение:
ОВК = 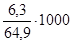 = 97 человека.
= 97 человека.
Следовательно, на каждые 1000 занятых в экономике России приходится 97 безработных.
ЗАДАЧА 4
Доходы пяти банков по операциям с ценными бумагами за отчетный период составили: 0,6; 0,7; 0,9; 1,1; 1,3 млн. руб. Определить средний доход банков по данной операции.
Решение: Средний доход пяти банков по операциям с ценными бумагами определим по средней арифметической простой:
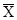 =
= 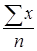 Средняя арифметическая простая
Средняя арифметическая простая
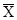 =
= 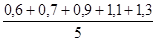 =
= 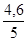 = 0,92 млн. руб.
= 0,92 млн. руб.
ЗАДАЧА 5
В трех партиях изделий с количеством 1200, 1800, 2400 штук обнаружен следующий процент брака: первая партия – 2,5%, вторая партия – 1,8%, третья партия – 0,5%. Требуется определить средний процент брака.
Средняя арифметическая взвешенная
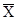 =
= 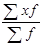 ,
,
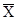 =
= 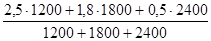 =
= 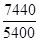 = 1,38%.
= 1,38%.
Следовательно, средний процент брака составляет 1,38%.
ЗАДАЧА 6
Таблица 1 - Доходы банков в отчетном году по кредитам
| № банка | процентная ставка, % | Доход банка, млн. руб. |
| 1 | 32 | 750 |
| 2 | 40 | 1200 |
| 3 | 38 | 800 |
Определить среднюю процентную ставку банков.
Решение: Средняя гармоническая взвешенная Средняя гармоническая взвешенная исчисляется по формуле:
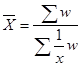 ,
,
где w= x f – объем признака, равный произведению вариант на частоты Основой выбора вида средней является реальное содержание определяемого показателя:
Процентная ставка = 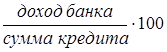 .
.
Средняя процентная ставка равна отношению доходов банков к сумме их кредита. В данном примере отсутствуют прямые данные о кредитах (f). Но их суммы можно определить косвенным путем, разделив доход банка (w) на процентную ставку (х). Средняя процентная ставка будет равна:
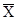 =
= 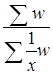 =
= 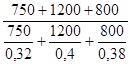 =
= 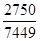 = 0,37 или 37,0%.
= 0,37 или 37,0%.
ЗАДАЧА 7 Средняя хронологическая - простая применяется в случае, если имеющиеся данные относятся к фиксированным моментам времени c равными интервалами
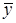 =
= 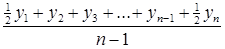 ,
,
где у – уровень ряда,
n – число уровней.
Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн. руб.:
на 1.01.2017г.– 500; на 1.02.2017 г. – 550; на 1.03.2017г. – 575; на 1.04.2017 г. – 560.
Определить средний остаток сырья и материалов на складе предприятия за I квартал.
Решение: По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:
 =
= 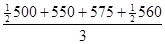 =551,7 млн. руб
=551,7 млн. руб
ЗАДАЧА 8 Мода – величина признака, которая наиболее часто встречается в данной совокупности.
В дискретном вариационном ряду мода определяется по наибольшей частоте.
В интервальном вариационном ряду мода определяется по формуле:
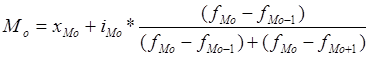
где 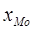 - нижняя граница модального интервала,
- нижняя граница модального интервала,
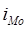 - величина модального интервала,
- величина модального интервала,
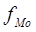 - частота модального интервала,
- частота модального интервала,
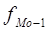 - частота интервала, предшествующего модальному,
- частота интервала, предшествующего модальному,
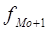 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Дата: 2019-07-30, просмотров: 698.