СЕМИНАРЫ
для студентов 211,212 ЭЗ (на 23.06.2019)
Тема 2 Статистическое наблюдение. Группировка, представление результатов статистического наблюдения
ЗАДАЧА 1. Произвести группировку работников по заработной плате с равными интервалами, образовав пять групп работников, если известно, что максимальная заработная плата на предприятии составляет 50 т.р., а минимальная 15 т.р.
Решение.
Определим величину интервала:
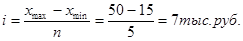
Группировка с равными закрытыми интервалами
| № группы | Группы работников по заработной плате, тыс. руб. |
| 1 | 15 - 22 |
| 2 | 22 – 29 |
| 3 | 29 - 36 |
| 4 | 36 - 43 |
| 5 | 43 - 50 |
ЗАДАЧА 2. Имеются данные о распределении предприятий по среднегодовой численности работающих по двум отраслям промышленности.
| Первая отрасль | Вторая отрасль | ||
| Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % | Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % |
| до 50 | 10 | до 100 | 25 |
| 50 – 100 | 15 | 100 – 250 | 30 |
| 100 – 200 | 20 | 250 – 400 | 35 |
| 200 – 300 | 30 | 400 - 600 | 10 |
| 300 – 600 | 18 | ||
| 600 – 1000 | 7 | ||
| Итого | 100 | Итого | 100 |
Необходимо произвести перегруппировку предприятий первой отрасли, взяв за основу распределение рабочих второй отрасли для сравнения структур отраслей по численности работающих. Результаты необходимо представить в таблице.
Решение.
| Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % | |
| Первая отрасль | Вторая отрасль | |
| до 100 | 10+15 = 25 | 25 |
| 100 – 250 | 20+½ * 30 = 35 | 30 |
| 250 – 400 | ½ *30+ 1/3 * 18 = 21 | 35 |
| 400 - 600 | 2/3 *18 = 12 | 10 |
| свыше 600 | 7 | - |
| Итого | 100 | 100 |
Вывод: численность рабочих на предприятиях первой отрасли более дифференцирована, чем на предприятиях второй отрасли.
ЗАДАЧА 3
Имеются следующие данные о деятельности коммерческих банков (выборка в случайном порядке).
Таблица 1 - Размеры процентных ставок и кредитов, предоставляемых коммерческими банками предприятиям, организациям
| № банка | Процентная ставка, % х | Кредиты, млн. руб. у |
| 1 | 2 | 3 |
| 1. | 20,2 | 9,54 |
| 2. | 17,3 | 13,56 |
| 3. | 14,2 | 22,33 |
| 4. | 11,5 | 27,43 |
| 5. | 17,1 | 13,58 |
| 6. | 23,6 | 3,25 |
| 7. | 11,0 | 27,70 |
| 8. | 14,5 | 21,20 |
| 9. | 17,5 | 13,50 |
| 10. | 24,0 | 2,50 |
Задание: постройте статистический ряд распределения банков по признаку размер процентной ставки (факторный признак Х), образовав три группы с равными интервалами.
Решение
Определим величину интервала (по ставке):
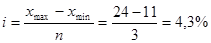
Построим расчетную таблицу: Таблица 2
Распределение банков по процентной ставке
| № п/п | Группы банков по размеру процентной ставки, % | № банка | Процентная ставка, % | Сумма кредита, млн. руб. |
| 1 | 2 | 3 | 4 | 5 |
| 1. | 11 – 15,3 | 3, 4, 7, 8 | 14,2+11,5+11+14,5 | 22,33+27,43+27,7+21,2 |
| Итого | 4 | 51,2 | 98,66 | |
| 2. | 15,3 – 19,6 | 2, 5,9 | 17,3+17,1+17,5 | 13,56+13,58+13,5 |
| Итого | 3 | 51,9 | 40,64 | |
| 3. | 19,6 – 24 | 1,6, 10 | 20,2+23,6+24 | 9,54+3,25+2,5 |
| Итого | 3 | 67,8 | 15,29 | |
| Всего | 10 | 170,9 | 154,59 |
Используя таблицу 2, строим аналитическую группировку, характеризующую зависимость между признаками.
Таблица 3
Зависимость суммы выданного банком кредита
от размера процентной ставки
| № п/п | Группы банков по размеру процентной ставки | Число банков | Процентная ставка, % | Сумма выданных кредитов, млн. руб | ||
| всего | в среднем на один банк (столб. 4/столб.3) | всего | в среднем на один банк (столб. 6/ столб. 3) | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1. | 11 – 15,3 | 4 | 51,2 | 12,80 | 98,66 | 24,67 |
| 2. | 15,3 – 19,6 | 3 | 51,9 | 17,30 | 40,64 | 13,55 |
| 3. | 19,6 – 24 | 3 | 67,8 | 22,60 | 15,29 | 5,10 |
| Итого | 10 | 170,9 | 17,09 | 154,59 | 15,459 | |
Вывод: Анализ данных табл. 3. показывает, что с ростом процентной ставки, под которую выдается банком кредит, средняя сумма кредита, выданная одним банком, уменьшается. Следовательно, между исследуемыми признаками существует обратная корреляционная зависимость.
ЗАДАЧА 4
Доходы пяти банков по операциям с ценными бумагами за отчетный период составили: 0,6; 0,7; 0,9; 1,1; 1,3 млн. руб. Определить средний доход банков по данной операции.
Решение: Средний доход пяти банков по операциям с ценными бумагами определим по средней арифметической простой:
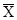 =
= 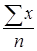 Средняя арифметическая простая
Средняя арифметическая простая
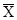 =
= 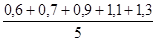 =
= 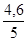 = 0,92 млн. руб.
= 0,92 млн. руб.
ЗАДАЧА 5
В трех партиях изделий с количеством 1200, 1800, 2400 штук обнаружен следующий процент брака: первая партия – 2,5%, вторая партия – 1,8%, третья партия – 0,5%. Требуется определить средний процент брака.
ЗАДАЧА 6
Таблица 1 - Доходы банков в отчетном году по кредитам
| № банка | процентная ставка, % | Доход банка, млн. руб. |
| 1 | 32 | 750 |
| 2 | 40 | 1200 |
| 3 | 38 | 800 |
Определить среднюю процентную ставку банков.
Решение: Средняя гармоническая взвешенная Средняя гармоническая взвешенная исчисляется по формуле:
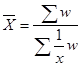 ,
,
где w= x f – объем признака, равный произведению вариант на частоты Основой выбора вида средней является реальное содержание определяемого показателя:
Процентная ставка = 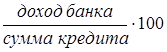 .
.
Средняя процентная ставка равна отношению доходов банков к сумме их кредита. В данном примере отсутствуют прямые данные о кредитах (f). Но их суммы можно определить косвенным путем, разделив доход банка (w) на процентную ставку (х). Средняя процентная ставка будет равна:
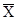 =
= 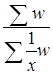 =
= 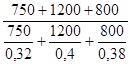 =
= 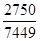 = 0,37 или 37,0%.
= 0,37 или 37,0%.
ЗАДАЧА 7 Средняя хронологическая - простая применяется в случае, если имеющиеся данные относятся к фиксированным моментам времени c равными интервалами
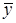 =
= 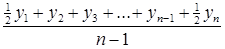 ,
,
где у – уровень ряда,
n – число уровней.
Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн. руб.:
на 1.01.2017г.– 500; на 1.02.2017 г. – 550; на 1.03.2017г. – 575; на 1.04.2017 г. – 560.
Определить средний остаток сырья и материалов на складе предприятия за I квартал.
Решение: По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:
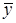 =
= 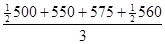 =551,7 млн. руб
=551,7 млн. руб
ЗАДАЧА 8 Мода – величина признака, которая наиболее часто встречается в данной совокупности.
В дискретном вариационном ряду мода определяется по наибольшей частоте.
В интервальном вариационном ряду мода определяется по формуле:
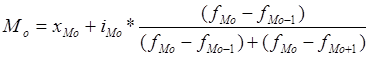
где 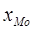 - нижняя граница модального интервала,
- нижняя граница модального интервала,
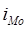 - величина модального интервала,
- величина модального интервала,
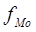 - частота модального интервала,
- частота модального интервала,
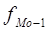 - частота интервала, предшествующего модальному,
- частота интервала, предшествующего модальному,
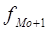 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
ЗАДАЧА 11
Таблица 1 - Группировка вкладчиков по размеру вклада в банке города
| Размер вклада, руб. | До 4000 | 4000-6000 | 6000-8000 | 8000-10000 | Св. 10000 |
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определить средний размер вклада и среднее квадратическое отклонение, дисперсию, коэффициент вариации. Сделать выводы.
Решение: Для расчета среднего размера вклада и среднего квадратического отклонения строим расчетную таблицу 2.
Открытые интервалы – закрвают исходя из шага поседующего или предшествующего закрытого интервала.
Открытый интервал «до 4000» – исходя из шага интервала (6000-4000)=2000, т.е.закрываем интервал 2000-4000.
Открытый интервал «всыше 10000» – исходя из шага интервала (10000-8000)=2000, т.е.закрываем интервал 10000-12000.
Преобразуем интервальный ряд динамики в моментный (исходя из расчета средних величин).
Таблица 2 - Расчет среднего квадратического отклонения
| Группы вкладчиков по размеру вклада, руб. х | Число вкладчи-ков f | xf |
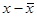
|
( 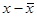 )2 )2
|
( 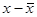 )2 f )2 f
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| (2000+4000)/2 =3000 5000 7000 9000 11000 | 32 56 120 104 88 | 96000 280000 840000 936000 968000 | 3000-7800= -4800 | (-4800)2=23040000 | 23040000*32=737280000 |
| Итого | 400 | 3120000 | – | – | 2304000000 |
Определим средний размер вклада:
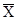 =
= 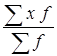 = 3120000/ 400= 7800 руб.
= 3120000/ 400= 7800 руб.
Определим среднее квадратическое отклонение – является абсолютной мерой вариации признака в совокупности и выражается в тех же единицах измерения варьирующего признака.
σ = 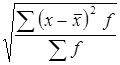 =
= 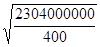 = 2400 руб.
= 2400 руб.
Дисперсия признака (σ2) Дисперсия - средняя арифметическая квадратов отклонений конкретных значений варьирующего признака от его средней арифметической.
Простая (общая) дисперсия
σ2 = 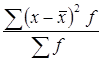 = 5760000
= 5760000
ЗАДАЧА
По результатам предварительных расчетов межгрупповая дисперсия между фактором х и у составила 16,9 кг, а общая дисперсия 21,3 кг.
Определить коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы.
η2 = 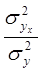 = 16,9/21,3 = 0,793
= 16,9/21,3 = 0,793
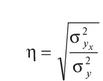 = Ö16,9/21,3= 0,89 или 89%
= Ö16,9/21,3= 0,89 или 89%
Вывод: Связь между факторами высокая, прямая
СЕМИНАРЫ
для студентов 211,212 ЭЗ (на 23.06.2019)
Тема 2 Статистическое наблюдение. Группировка, представление результатов статистического наблюдения
ЗАДАЧА 1. Произвести группировку работников по заработной плате с равными интервалами, образовав пять групп работников, если известно, что максимальная заработная плата на предприятии составляет 50 т.р., а минимальная 15 т.р.
Решение.
Определим величину интервала:
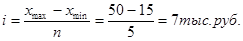
Группировка с равными закрытыми интервалами
| № группы | Группы работников по заработной плате, тыс. руб. |
| 1 | 15 - 22 |
| 2 | 22 – 29 |
| 3 | 29 - 36 |
| 4 | 36 - 43 |
| 5 | 43 - 50 |
ЗАДАЧА 2. Имеются данные о распределении предприятий по среднегодовой численности работающих по двум отраслям промышленности.
| Первая отрасль | Вторая отрасль | ||
| Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % | Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % |
| до 50 | 10 | до 100 | 25 |
| 50 – 100 | 15 | 100 – 250 | 30 |
| 100 – 200 | 20 | 250 – 400 | 35 |
| 200 – 300 | 30 | 400 - 600 | 10 |
| 300 – 600 | 18 | ||
| 600 – 1000 | 7 | ||
| Итого | 100 | Итого | 100 |
Необходимо произвести перегруппировку предприятий первой отрасли, взяв за основу распределение рабочих второй отрасли для сравнения структур отраслей по численности работающих. Результаты необходимо представить в таблице.
Решение.
| Группировка предприятий по численности рабочих, чел. | Удельный вес предприятий, % | |
| Первая отрасль | Вторая отрасль | |
| до 100 | 10+15 = 25 | 25 |
| 100 – 250 | 20+½ * 30 = 35 | 30 |
| 250 – 400 | ½ *30+ 1/3 * 18 = 21 | 35 |
| 400 - 600 | 2/3 *18 = 12 | 10 |
| свыше 600 | 7 | - |
| Итого | 100 | 100 |
Вывод: численность рабочих на предприятиях первой отрасли более дифференцирована, чем на предприятиях второй отрасли.
ЗАДАЧА 3
Имеются следующие данные о деятельности коммерческих банков (выборка в случайном порядке).
Таблица 1 - Размеры процентных ставок и кредитов, предоставляемых коммерческими банками предприятиям, организациям
| № банка | Процентная ставка, % х | Кредиты, млн. руб. у |
| 1 | 2 | 3 |
| 1. | 20,2 | 9,54 |
| 2. | 17,3 | 13,56 |
| 3. | 14,2 | 22,33 |
| 4. | 11,5 | 27,43 |
| 5. | 17,1 | 13,58 |
| 6. | 23,6 | 3,25 |
| 7. | 11,0 | 27,70 |
| 8. | 14,5 | 21,20 |
| 9. | 17,5 | 13,50 |
| 10. | 24,0 | 2,50 |
Задание: постройте статистический ряд распределения банков по признаку размер процентной ставки (факторный признак Х), образовав три группы с равными интервалами.
Решение
Определим величину интервала (по ставке):
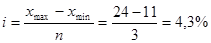
Построим расчетную таблицу: Таблица 2
Распределение банков по процентной ставке
| № п/п | Группы банков по размеру процентной ставки, % | № банка | Процентная ставка, % | Сумма кредита, млн. руб. |
| 1 | 2 | 3 | 4 | 5 |
| 1. | 11 – 15,3 | 3, 4, 7, 8 | 14,2+11,5+11+14,5 | 22,33+27,43+27,7+21,2 |
| Итого | 4 | 51,2 | 98,66 | |
| 2. | 15,3 – 19,6 | 2, 5,9 | 17,3+17,1+17,5 | 13,56+13,58+13,5 |
| Итого | 3 | 51,9 | 40,64 | |
| 3. | 19,6 – 24 | 1,6, 10 | 20,2+23,6+24 | 9,54+3,25+2,5 |
| Итого | 3 | 67,8 | 15,29 | |
| Всего | 10 | 170,9 | 154,59 |
Используя таблицу 2, строим аналитическую группировку, характеризующую зависимость между признаками.
Таблица 3
Зависимость суммы выданного банком кредита
от размера процентной ставки
| № п/п | Группы банков по размеру процентной ставки | Число банков | Процентная ставка, % | Сумма выданных кредитов, млн. руб | ||
| всего | в среднем на один банк (столб. 4/столб.3) | всего | в среднем на один банк (столб. 6/ столб. 3) | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1. | 11 – 15,3 | 4 | 51,2 | 12,80 | 98,66 | 24,67 |
| 2. | 15,3 – 19,6 | 3 | 51,9 | 17,30 | 40,64 | 13,55 |
| 3. | 19,6 – 24 | 3 | 67,8 | 22,60 | 15,29 | 5,10 |
| Итого | 10 | 170,9 | 17,09 | 154,59 | 15,459 | |
Вывод: Анализ данных табл. 3. показывает, что с ростом процентной ставки, под которую выдается банком кредит, средняя сумма кредита, выданная одним банком, уменьшается. Следовательно, между исследуемыми признаками существует обратная корреляционная зависимость.
Дата: 2019-07-30, просмотров: 552.