Анализируя процессы переработки полимеров, часто приходится встречаться с задачей о нагреве или охлаждении полимера, сопровождающемся изменением физического состояния (плавлением или затвердением). Теоретическое рассмотрение задач такого типа впервые выполнено Нейманном.

Мы остановимся только на одном, наиболее простом случае, в котором для упрощения теплофизические характеристики расплава и твердого полимера будем считать одинаковыми. Пусть скрытая теплота плавления равна λ, а температура плавления Тп. Обозначим координату поверхности раздела между твердой и жидкой фазами через Х(t). Тогда одно из граничных условий которое должно удовлетворяться на этой поверхности, запишется в виде:

                                     Ts = Tm = Tn при X=X(t)                                  (2.24)

Индекс s указывает, что соответствующая величина относится к твердой фазе (например, ρs — плотность твердой фазы). Соответственно индекс m указывает, что величина относится к жидкой фазе.

Второе граничное условие касается поглощения (или выделения) скрытой теплоты на поверхности раздела. Предположим, что в области x > x ( t ) находится жидкость при температуре Т_т(х, t ), а в области x = x ( t ) — твердая фаза при температуре T_s ( x_tt ).

Если поверхность раздела перемещается на расстояние dx, то в элементе объема вещества выделяется и должно быть отведено в результате теплопроводности количество тепла, в пересчете на единицу поверхности равное lρdx. Математически это условие за­пишется в виде:

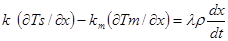                        (2.25)

Рассмотрим три случая: плавление, затвердевание и плавление с удалением расплава.

2.3.1. Плавление в области х > 0.

Если в начальный момент область х > 0 занята твердым телом с постоянной температурой T_{s 0} и при t > 0 плоскость х = 0 поддерживается при постоянной темпера­туре Т₂ > Т_п, то положение плоскости плавления определится вы­ражением:

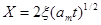                                                                        (2.26)

Здесь 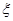 - корень уравнения

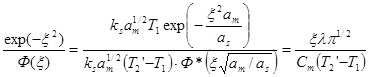      (2.27)

    где

;

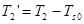При этом распределение температур в твёрдой и жидкой фазах описывается выражением:

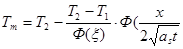                                                       (2.28)

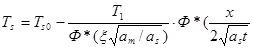                  (2.29)

Затвердевание.

 Пусть в начальный момент времени область х > 0 представляет собой жидкость, а область х <С 0 — твердое тело. Иначе говоря, в начальный момент поверхность раздела сов­падает с началом координат.

Допустим, что значения термических коэффициентов только что затвердевшего расплава отличаются от значений термических коэффициентов твердой фазы в области х < 0. Присвоим термиче­ским коэффициентам этой области индекс s₀.

Поступающий расплав имеет температуру Т₂. Координата по­верхности раздела фаз определится соотношением:

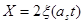                                                     (2.30)

Здесь ξ — корень уравнения

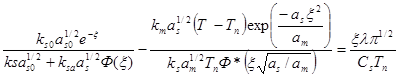    (2.31)

После определения ξ, которое может быть выполнено любым численным методом (например, методом итерации), можно опре­делить температурные поля во всех трех областях (начальная твердая фаза, затвердевшее вещество и расплав):

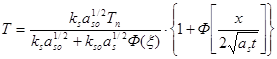                                  (2.34)

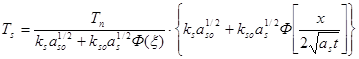                 (2.35)

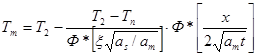                                      (2.35)