РЕФЕРАТ
Данная курсовая работа содержит 26 листов печатного текста, 7 рисунков, 66 формул.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, ДИФЕРИНЦИАЛЬНОЕ УРАВНЕНИЕ, ТЕПЛОПРОВОДНОСТЬ, ВРЕМЯ, ЛИТНИКОВЫЙ КАНАЛ, ОХЛАЖДЕНИЕ, ТЕМПЕРАТУРНОЕ ПОЛЕ.
Курсовая работа содержит расчет температурного поля литникового канала литьевой формы, теоретические сведения о процессах происходящих в химической технологии связанных с охлаждением и нагреванием материалов, построение математической модели описывающую теплообмен между бесконечно-длинным цилиндром и его поверхностью, описание переменных входящих в модель. Разработана программа описывающая охлаждение полистирольного литника формы.
СОДЕРЖАНИЕ
РЕФЕРАТ... 2
СОДЕРЖАНИЕ... 3
ВВЕДЕНИЕ... 4
1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ.... 5
1.1 Неограниченный цилиндр.. 5
1.2 Описание переменных... 5
1.3 Граничные условия.. 5
2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.... 6
2.1 Теплообмен... 6
2.1.1 Теплопроводность.. 6
2.1.2. Теплопередача в стационарном режиме.. 7
2.1.3. Нестационарная теплопроводность.. 7
2.2. Нагревание и охлаждение тел простой геометрической формы... 8
2.2.1. Плоская неограниченная пластина.. 8
2.2.2 Неограниченный цилиндр.. 10
2.3. Теплопроводность в процессах, сопровождающихся изменением физического состояния.. 11
2.3.1. Плавление в области х > 0.. 12
2.3.2. Затвердевание.. 12
2.3.3 Плавление с непрерывным удалением расплава.. 13
2.4.Теплопередача в потоках расплава... 13
2.5. Лучистый теплообмен... 15
3. СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ИССЛЕДУЕМОГО ПРОЦЕССА.. 17
3.1. Специфика построения математических моделей описывающих термодинамические процессы... 17
3.2. Вывод дифференциального уравнения теплопроводности.. 17
4 СОСТАВЛЕНИЕ АЛГОРИТМА.... 20
5 СОСТАВЛЕНИЕ ПРОГРАММЫ..... 22
6 АНАЛИЗ МОДЕЛИРОВАНИЯ И РАСЧЁТОВ... 24
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ..... 25
ПРИЛОЖЕНИЕ1.. 26
ПРИЛОЖЕНИЕ2.. 27
ВВЕДЕНИЕ
Переработка полимерных материалов — это совокупность технологических приемов, методов и процессов, посредством которых исходный полимер превращают в различные изделия с заданными эксплуатационными характеристиками.
Полимеры начали перерабатывать в конце XIX в., а к середине XX в. переработка полимеров выделилась в самостоятельную область техники, в которой используется специализированное высокопроизводительное оборудование, необходимое для реализации в промышленных масштабах специфических для полимеров технологических процессов.
Вследствие большой производительности современного перерабатывающего оборудования и высокой стоимости технологических линий проведение экспериментальных исследований реального процесса переработки полимеров, даже осуществленных с применением современных методов экстремального планирования, превращается в дорогостоящую и продолжительную работу. Поэтому целесообразно изучать особенность каждого конкретного процесса, рассматривая вначале его теоретическое описание, т. е. его математическую модель.
При таком подходе в каждом конкретном случае этапу физического эксперимента (будь то создание несложной установки, конструирование технологической линии или опробование нового технологического режима) всегда предшествует этап теоретического эксперимента. На этом этапе нет необходимости прибегать к реальным экспериментам, вместо этого исследуются количественные характеристики процесса, полученные расчетным методом.
Такой подход позволяет существенно снизить объем физического эксперимента, поскольку прибегать к нему приходится на самой последней стадии — не в процессе поиска основных закономерностей, а для проверки и уточнения выданных рекомендаций. Разумеется, для того чтобы исследуемые теоретические модели процессов описывали эти процессы с достаточно хорошим приближением, они непременно должны учитывать основные особенности моделируемых явлении.
При математическом описании реальных производственных процессов приходится прибегать к существенным упрощениям. При этом значительную помощь в создании математических моделей оказывает анализ простых случаев. Прием такого рода вполне допустим, он позволяет независимо устанавливать основные закономерности наиболее простых случаев выбранных в качестве математического аналога поведения полимерных расплавов.
Термодинамические соотношения, описывающие разогрев и плавление полимеров, являются фундаментом, на базе которого строятся неизотермические модели реальных процессов переработки. Основные вопросы термодинамики и теплопередачи в полимерах рассмотрены в данной работе.
 1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ
1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ
Неограниченный цилиндр.
Рассмотрим неограниченный цилиндр радиуса R, температура поверхности которого остается неизменной на протяжении всего процесса теплообмена. Радиальное распределение температур в начальный момент задано в виде некоторой функции Т(r). Необходимо найти распределение температур. Такие задачи встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.
Дифференциальное уравнение теплопроводности для цилиндра имеет вид:
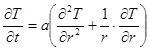 (1.1)
(1.1)
Краевые условия: 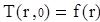 (1.2)
(1.2)
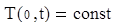 (1.3)
(1.3)
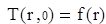 (1.4)
(1.4)
Решение, полученное методом разделения переменных, имеет сложный вид потому задачей данной работы является найти численное его решение.
Описание переменных
Уравнение теплопроводности устанавливает зависимость между следующими величинами характеризующими процесс теплопроводности:
T-температура по Цельсию (градус)
r-радиус цилиндра (М)
t-время (С)
a-коэффициент температуропроводности (градус/с*м2)
Граничные условия
Для решения данного дифференциального уравнения в частных производных необходимыми данными является значения производных температуры по радиусу на оси цилиндра, которая должна быть равной нулю (1.4).
Температуру стенки цилиндра, через которую происходит охлаждение литника примем равной 30 градусов.
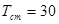 (1.5)
(1.5)
Радиус литника обычно составляет 0.01 м.
R=0.01 (1.6)
Распределение температуры в начальный момент времени по радиусу задано в виде убывающей экспоненциальной функции, чтобы производная температуры по
времени на оси цилиндра была равной нулю, радиус возводим в квадрат (1.7)
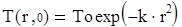 (1.7)
(1.7)
 2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Теплообмен
Различают три вида теплообмена: теплопроводность, теплопередача конвекцией и лучистый теплообмен.
Передача тепла за счет теплопроводности осуществляется в результате движения молекул, атомов и электронов; она играет значительную роль при теплообмене в твердых и расплавленных полимерах. При конвекции, которая возможна только в жидкостях и газах, тепло передается за счет относительного движения частиц нагретого тела. При лучистом теплообмене передача тепла между пространственно разделенными частями тела происходит за счет электромагнитного излучения.
Теплопроводность
Основной задачей теории теплопроводности является установление распределения температур внутри тела. Если распределение температур не зависит от времени, то задача теплопроводности является стационарной; если распределение температур зависит от времени, то задача становится нестационарной.
Передача тепла происходит во всех случаях, когда в теле существует температурный градиент. По закону Фурье, который лежит в основе всех расчетов теплопроводности, для изотропных материалов вектор теплового потока q пропорционален температурному градиенту:
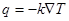 (2.1)
(2.1)
где q — количество тепла, проходящего через единичную поверхность, перпендикулярную направлению теплового потока;
k — коэффициент теплопроводности.
Полагая в уравнении энергетического баланса V = О, получим:
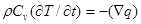 (2.2)
(2.2)
Уравнение (2.2) представляет собой уравнение теплопроводности для изотропного твердого тела.
Если внутри изотропного тела имеется источник тепла, то уравнение (2.2) необходимо дополнить членом, учитывающим тепловыделение
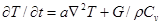 (2.3)
(2.3)
где  — коэффициент температуропроводности [замена
— коэффициент температуропроводности [замена 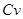 на
на  в уравнении (2.3) возможна для несжимаемых твердых тел];
в уравнении (2.3) возможна для несжимаемых твердых тел];
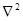 — оператор Лапласа в прямоугольной системе координат
— оператор Лапласа в прямоугольной системе координат
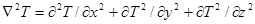 (2.4)
(2.4)
G — интенсивность внутренних тепловыделений, отнесенная к единице объема.
Примерами внутренних тепловыделений являются поглощения инфракрасного излучения в полупрозрачных средах, экзотермический эффект химических реакций и т. п.
Неограниченный цилиндр.
Рассмотрим неограниченный цилиндр радиуса R, температура поверхности которого остается неизменной на протяжении всего процесса теплообмена. Радиальное распределение температур в начальный момент задано в виде некоторой функции Т( r ). Необходимо найти распределение температур определения в цилиндре в любой момент времени. Задачи такого типа встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.
Дифференциальное уравнение теплопроводности для цилиндра
имеет вид: 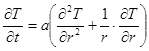 (2.19)
(2.19)
Краевые условия:
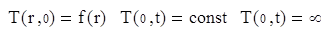
Решение, полученное методом разделения переменных, в безразмерной форме, имеет вид:
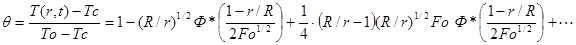 (2.20)
(2.20)
Для оценки изменения теплосодержания цилиндра определим среднюю температуру как:
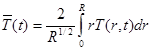 (2.21)
(2.21)
Тогда безразмерная средняя температура определится соотношением: 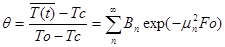 (2.22)
(2.22)
где 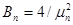 ;
; 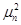 - корни функции Бесселя первого рода нулевого порядка определяемые выражением:
- корни функции Бесселя первого рода нулевого порядка определяемые выражением:
 (2.23)
(2.23)
Таким образом, уменьшение средней температуры описывается простым экспоненциальным законом. Для удобства прикидочных расчетов на рис. IV. 10 приведена номограмма зависимости между q и Fo.
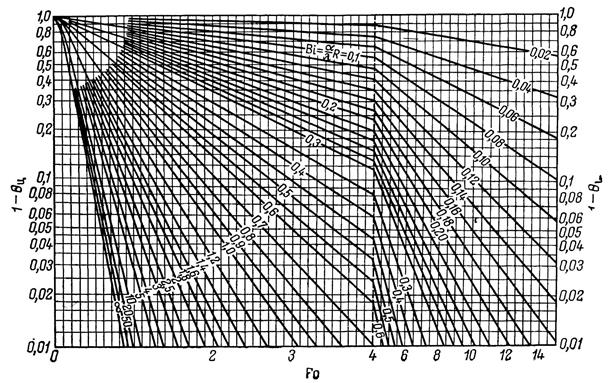
Рис. 2.5 Номограмма для определения зависимости между безразмерной средней избыточной температурой и критерием Фурье в случае неограниченного цилиндра.
Затвердевание.
Пусть в начальный момент времени область х > 0 представляет собой жидкость, а область х <С 0 — твердое тело. Иначе говоря, в начальный момент поверхность раздела совпадает с началом координат.
Допустим, что значения термических коэффициентов только что затвердевшего расплава отличаются от значений термических коэффициентов твердой фазы в области х < 0. Присвоим термическим коэффициентам этой области индекс s0.
Поступающий расплав имеет температуру Т2. Координата поверхности раздела фаз определится соотношением:
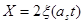 (2.30)
(2.30)
Здесь ξ — корень уравнения
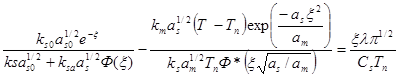 (2.31)
(2.31)
После определения ξ, которое может быть выполнено любым численным методом (например, методом итерации), можно определить температурные поля во всех трех областях (начальная твердая фаза, затвердевшее вещество и расплав):
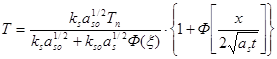 (2.34)
(2.34)
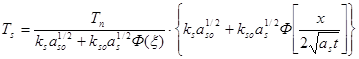 (2.35)
(2.35)
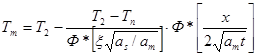 (2.35)
(2.35)
Лучистый теплообмен
Нагрев излучением применяется главным образом в операциях, предшествующих пневмо- и вакуум-формованию относительно тонких листов термопластов.
Лучистая энергия передается в виде электромагнитных волн, распространяющихся в пространстве до тех пор, пока на их пути не встретится какая-либо поглощающая среда: газ, жидкость или твердое тело. Излучаемая энергия пропорциональна четвертой степени абсолютной температуры изучающего тела. Так как обычно большая часть энергии излучения в применяемой на практике области температур приходится на инфракрасный спектр, нагрев излучением называют также инфракрасным нагревом.
Гипотетическое тело, поглощающее все падающие на него лучи, называется абсолютно черным телом. Интенсивность лучеиспускания абсолютно черного тела Еb определяется законом Стефана — Больцмана:
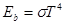 (2.43)
(2.43)
Где а — постоянная Стефана Больцмана, равная 1,36 • 10 -12 кал/(см2 • с • /K4), или 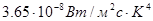
Реальные тела излучают меньше энергии. Их излучательная способность е оценивается по формуле:
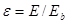 (2.44)
(2.44)
где Е — интенсивность лучеиспускания реального тела.
Обычно ε зависит от температуры, увеличиваясь с ее ростом. Металлоиды и окислы металлов обладают высокой излучательной способностью (ε ≥ 0,8). У хорошо отполированных металлов излучательная способность невысока (ε ≤ 0,1) Реальные тела поглощают только часть попадающего на них излучения.
Коэффициент поглощения определяется как отношение поглощенного из лучения к падающему.
При расчете лучистого теплообмена между черными телами под излучение попадает только та часть тела, которая просматривается с излучающего тела. Далее, интенсивность излучаемой энергии максимальна вдоль нормали к поверхности и равна нулю в тангенциальном направлении. Можно учесть взаимное расположение излучателя и облучаемого тела введением коэффициента видимости, учитывающего долю излучаемой энергии, которая попадает на облучаемое тело.
Допустим, что лучистая энергия, излучаемая от черной поверхности 1 на черную поверхность 2, равна E1A1F12 (A1 — площадь излучателя, F12 — доля энергии, попадающая на поверхность 2). Очевидно, что
A 1 F 12 = A 2 F 21 (2.45)
Поэтому количество тепла Q 12, переданное при лучистом теплообмене от тела 1 к телу 2, равно:
Q 12 = A 1 F 12 ( E 1 - E 2 ) (2.46)
Воспользуемся законом Стефана — Больцмана и получим:
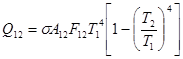 (2.47)
(2.47)
Наконец, если T 2 / T 1 << 1 то выражение (2.47) сводится к виду:
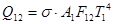 (2.48)
(2.48)
Для неабсолютно черных тел расчет осложняется наличием доли многократно отраженного излучения. В случае двух бесконечных параллельных пластин общее количество тепла, переданного с единицы поверхности, выражается формулой:
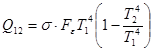 (2.49)
(2.49)
где Fε — коэффициент излучения, равный:
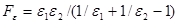 (2.50)
(2.50)
Коэффициент теплопередачи h определится из выражения, аналогичного по форме уравнению Ньютона:
 (2.51)
(2.51)
Реальные полимеры и их расплавы плохо пропускают инфракрасное излучение. Поэтому падающая на них энергия превращается в тепло непосредственно на их поверхности. Некоторое количество выделяющегося тепла сразу же теряется на потери в виде собственного излучения и путем конвекции.
Поглощаемое тепло распространяется внутрь за счет процессов теплопроводности. Поэтому итоговое распределение температур в теле, нагреваемом лучистой энергией, зависит не только от мощности потока лучистой энергии, но также и от теплопроводности и конвективных потерь.
ПРИЛОЖЕНИЕ1
 clear, clc, clf, clg
clear, clc, clf, clg
t0=0;
tk=120;
nt=120;
Tc=30;
Tpol=170;
nR=10;
R=0.01;
dr=R/(nR-1);
dt=(tk-t0)/(nt-1);
a=0.00000056;
for i=1:nt+1
T(i,1)=Tc;
end
for j=1:nR+2
T(1,j)=Tpol*exp(-2000*(R-dr*(j-1))^2);
end
for i=1:nt
for j=1:nR
r=R-dr*(j-1)+0.0001*dr;
T(i+1,j+1)=T(i,j+1)+(a*dt/dr)*(((T(i,j+2)-2*T(i,j+1)+T(i,j))/dr)+((1/r)*(T(i,j+2)-T(i,j+1))));
end
T(i+1,nR+1)=T(i+1,nR);
T(i+1,nR+2)=T(i+1,nR);
end
for i=1:nt
for j=1:nR
TT(i,j)=T(i,nR-j+1);
end
end
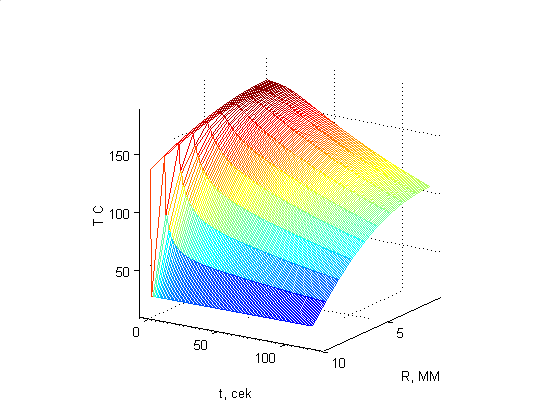
figure(1)
mesh(TT)
xlabel('R, MM')
ylabel('t, cek')
zlabel('T C') 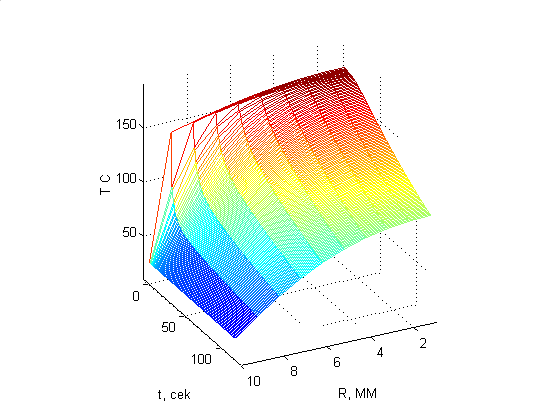
ПРИЛОЖЕНИЕ2

РЕФЕРАТ
Данная курсовая работа содержит 26 листов печатного текста, 7 рисунков, 66 формул.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, ДИФЕРИНЦИАЛЬНОЕ УРАВНЕНИЕ, ТЕПЛОПРОВОДНОСТЬ, ВРЕМЯ, ЛИТНИКОВЫЙ КАНАЛ, ОХЛАЖДЕНИЕ, ТЕМПЕРАТУРНОЕ ПОЛЕ.
Курсовая работа содержит расчет температурного поля литникового канала литьевой формы, теоретические сведения о процессах происходящих в химической технологии связанных с охлаждением и нагреванием материалов, построение математической модели описывающую теплообмен между бесконечно-длинным цилиндром и его поверхностью, описание переменных входящих в модель. Разработана программа описывающая охлаждение полистирольного литника формы.
СОДЕРЖАНИЕ
РЕФЕРАТ... 2
СОДЕРЖАНИЕ... 3
ВВЕДЕНИЕ... 4
1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ.... 5
1.1 Неограниченный цилиндр.. 5
1.2 Описание переменных... 5
1.3 Граничные условия.. 5
2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.... 6
2.1 Теплообмен... 6
2.1.1 Теплопроводность.. 6
2.1.2. Теплопередача в стационарном режиме.. 7
2.1.3. Нестационарная теплопроводность.. 7
2.2. Нагревание и охлаждение тел простой геометрической формы... 8
2.2.1. Плоская неограниченная пластина.. 8
2.2.2 Неограниченный цилиндр.. 10
2.3. Теплопроводность в процессах, сопровождающихся изменением физического состояния.. 11
2.3.1. Плавление в области х > 0.. 12
2.3.2. Затвердевание.. 12
2.3.3 Плавление с непрерывным удалением расплава.. 13
2.4.Теплопередача в потоках расплава... 13
2.5. Лучистый теплообмен... 15
3. СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ИССЛЕДУЕМОГО ПРОЦЕССА.. 17
3.1. Специфика построения математических моделей описывающих термодинамические процессы... 17
3.2. Вывод дифференциального уравнения теплопроводности.. 17
4 СОСТАВЛЕНИЕ АЛГОРИТМА.... 20
5 СОСТАВЛЕНИЕ ПРОГРАММЫ..... 22
6 АНАЛИЗ МОДЕЛИРОВАНИЯ И РАСЧЁТОВ... 24
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ..... 25
ПРИЛОЖЕНИЕ1.. 26
ПРИЛОЖЕНИЕ2.. 27
ВВЕДЕНИЕ
Переработка полимерных материалов — это совокупность технологических приемов, методов и процессов, посредством которых исходный полимер превращают в различные изделия с заданными эксплуатационными характеристиками.
Полимеры начали перерабатывать в конце XIX в., а к середине XX в. переработка полимеров выделилась в самостоятельную область техники, в которой используется специализированное высокопроизводительное оборудование, необходимое для реализации в промышленных масштабах специфических для полимеров технологических процессов.
Вследствие большой производительности современного перерабатывающего оборудования и высокой стоимости технологических линий проведение экспериментальных исследований реального процесса переработки полимеров, даже осуществленных с применением современных методов экстремального планирования, превращается в дорогостоящую и продолжительную работу. Поэтому целесообразно изучать особенность каждого конкретного процесса, рассматривая вначале его теоретическое описание, т. е. его математическую модель.
При таком подходе в каждом конкретном случае этапу физического эксперимента (будь то создание несложной установки, конструирование технологической линии или опробование нового технологического режима) всегда предшествует этап теоретического эксперимента. На этом этапе нет необходимости прибегать к реальным экспериментам, вместо этого исследуются количественные характеристики процесса, полученные расчетным методом.
Такой подход позволяет существенно снизить объем физического эксперимента, поскольку прибегать к нему приходится на самой последней стадии — не в процессе поиска основных закономерностей, а для проверки и уточнения выданных рекомендаций. Разумеется, для того чтобы исследуемые теоретические модели процессов описывали эти процессы с достаточно хорошим приближением, они непременно должны учитывать основные особенности моделируемых явлении.
При математическом описании реальных производственных процессов приходится прибегать к существенным упрощениям. При этом значительную помощь в создании математических моделей оказывает анализ простых случаев. Прием такого рода вполне допустим, он позволяет независимо устанавливать основные закономерности наиболее простых случаев выбранных в качестве математического аналога поведения полимерных расплавов.
Термодинамические соотношения, описывающие разогрев и плавление полимеров, являются фундаментом, на базе которого строятся неизотермические модели реальных процессов переработки. Основные вопросы термодинамики и теплопередачи в полимерах рассмотрены в данной работе.
 1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ
1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ
Неограниченный цилиндр.
Рассмотрим неограниченный цилиндр радиуса R, температура поверхности которого остается неизменной на протяжении всего процесса теплообмена. Радиальное распределение температур в начальный момент задано в виде некоторой функции Т(r). Необходимо найти распределение температур. Такие задачи встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.
Дифференциальное уравнение теплопроводности для цилиндра имеет вид:
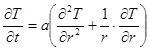 (1.1)
(1.1)
Краевые условия: 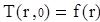 (1.2)
(1.2)
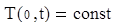 (1.3)
(1.3)
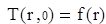 (1.4)
(1.4)
Решение, полученное методом разделения переменных, имеет сложный вид потому задачей данной работы является найти численное его решение.
Описание переменных
Уравнение теплопроводности устанавливает зависимость между следующими величинами характеризующими процесс теплопроводности:
T-температура по Цельсию (градус)
r-радиус цилиндра (М)
t-время (С)
a-коэффициент температуропроводности (градус/с*м2)
Граничные условия
Для решения данного дифференциального уравнения в частных производных необходимыми данными является значения производных температуры по радиусу на оси цилиндра, которая должна быть равной нулю (1.4).
Температуру стенки цилиндра, через которую происходит охлаждение литника примем равной 30 градусов.
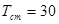 (1.5)
(1.5)
Радиус литника обычно составляет 0.01 м.
R=0.01 (1.6)
Распределение температуры в начальный момент времени по радиусу задано в виде убывающей экспоненциальной функции, чтобы производная температуры по
времени на оси цилиндра была равной нулю, радиус возводим в квадрат (1.7)
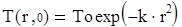 (1.7)
(1.7)
 2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
2 ОБЩИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Теплообмен
Различают три вида теплообмена: теплопроводность, теплопередача конвекцией и лучистый теплообмен.
Передача тепла за счет теплопроводности осуществляется в результате движения молекул, атомов и электронов; она играет значительную роль при теплообмене в твердых и расплавленных полимерах. При конвекции, которая возможна только в жидкостях и газах, тепло передается за счет относительного движения частиц нагретого тела. При лучистом теплообмене передача тепла между пространственно разделенными частями тела происходит за счет электромагнитного излучения.
Теплопроводность
Основной задачей теории теплопроводности является установление распределения температур внутри тела. Если распределение температур не зависит от времени, то задача теплопроводности является стационарной; если распределение температур зависит от времени, то задача становится нестационарной.
Передача тепла происходит во всех случаях, когда в теле существует температурный градиент. По закону Фурье, который лежит в основе всех расчетов теплопроводности, для изотропных материалов вектор теплового потока q пропорционален температурному градиенту:
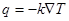 (2.1)
(2.1)
где q — количество тепла, проходящего через единичную поверхность, перпендикулярную направлению теплового потока;
k — коэффициент теплопроводности.
Полагая в уравнении энергетического баланса V = О, получим:
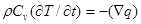 (2.2)
(2.2)
Уравнение (2.2) представляет собой уравнение теплопроводности для изотропного твердого тела.
Если внутри изотропного тела имеется источник тепла, то уравнение (2.2) необходимо дополнить членом, учитывающим тепловыделение
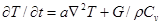 (2.3)
(2.3)
где  — коэффициент температуропроводности [замена
— коэффициент температуропроводности [замена 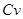 на
на  в уравнении (2.3) возможна для несжимаемых твердых тел];
в уравнении (2.3) возможна для несжимаемых твердых тел];
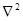 — оператор Лапласа в прямоугольной системе координат
— оператор Лапласа в прямоугольной системе координат
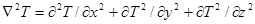 (2.4)
(2.4)
G — интенсивность внутренних тепловыделений, отнесенная к единице объема.
Примерами внутренних тепловыделений являются поглощения инфракрасного излучения в полупрозрачных средах, экзотермический эффект химических реакций и т. п.
Теплопередача в стационарном режиме.
Теплопередачу в непрерывно действующих нагревательных системах перерабатывающего оборудования можно рассматривать как независящую от времени. Следовательно, распределение температур носит установившийся характер и определяется интегрированием дифференциального уравнения (2.5)
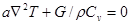 (2.5)
(2.5)
Дата: 2019-07-30, просмотров: 356.