Под неограниченной обычно понимают такую пластину, ширина и длина которой во много раз превышают толщину. Таким образом, неограниченная пластина (рис. 2.1) представляет собой тело, ограниченное двумя параллельными плоскостями. Изменение температуры происходит только в одном направлении (х), в двух других направлениях (у и z) температура неизменна.

Рис. 2.1. Положение координат при исследовании теплового процесса в неограниченной пластине.

Следовательно, задача является одномерной. Для одномерного теплового потока без внутреннего источника тепла уравнение теплопроводности сводится к виду: 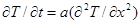                                                                     (2.11)

Обычно используют граничные условия третьего рода:

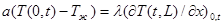                    (2.12)

Рассмотрим случай, когда в начальный момент температура пластины во всех точках была одинакова и равна То. Это начальное условие записывается в виде:

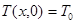                                                                                   (2.13)

Решение, полученное методом преобразования Лапласа, имеет вид:

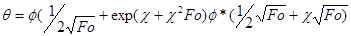(2.14)

Здесь 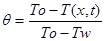— безразмерная температура;

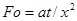— критерий Фурье (критерий гомохронности для процессов чистой теплопроводности );

- безразмерная координата;

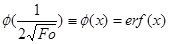— функция ошибок, где ;

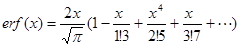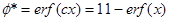
Если коэффициент теплоотдачи очень велик (это эквивалентно заданию постоянной температуры на стенке), уравнение (2.14) упрощается:

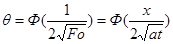                                                                              (2.15)

Для прикидочных расчетов удобно пользоваться номограммой зависимости q от   представленной на рис.2.2 

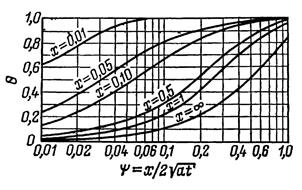
Рис.2.2 Номограмма для определения безразмеоной температуры в сечении неограниченной пластины при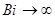

Если значение критерия Фурье велико, но не равно бесконечности, решение имеет вид:

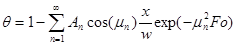                                                                 (2.16)

Здесь                                                     (2.17)

где 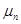— корни характеристического уравнения

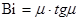                                                 (2.18)

где Bi = aw/l — критерий Био.

Уравнение (2.18) имеет бесчисленное множество действительных положительных корней. Первые пять корней для различных значений критерия Био были вычислены Карслоу и Егером. Обычно на практике пользуются номограммами. Номограмма позволяющая определить безразмерную температуру при различных значениях критерях Био приведена на рис.2.3

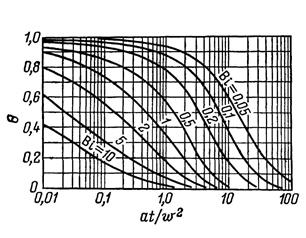
Рис. 2.3 Номограмма для определения безразмерной температуры поверхности неограниченной пластины.

Ана­логичная номограмма, предназ­наченная для определения тем­пературы в центре пластины, при­ведена на рис.2.4.

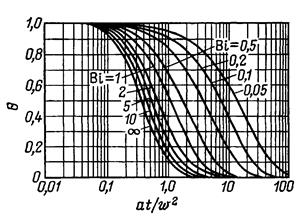
Рис. 2.4 Номограмма для определения безразмерной температуры в середине неограниченной пластины

Неограниченный цилиндр.

Рас­смотрим неограниченный цилиндр радиуса R, температура поверх­ности которого остается неизмен­ной на протяжении всего процес­са теплообмена. Радиальное рас­пределение температур в началь­ный момент задано в виде некоторой функции Т( r ). Необходимо найти распределение температур определения в цилиндре в любой момент времени. Задачи такого типа встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.

Дифференциальное уравнение теплопроводности для цилиндра

имеет вид: 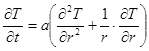                                       (2.19)

Краевые условия:  

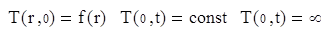
Решение, полученное методом разделения переменных, в без­размерной форме, имеет вид:

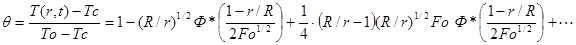    (2.20)

Для оценки изменения теплосодержания цилиндра определим среднюю температуру как:

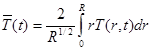                                                                                  (2.21)

Тогда безразмерная средняя температура определится соотноше­нием: 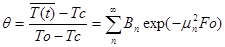                                             (2.22)

где 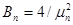; 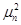- корни функции Бесселя первого рода нулевого порядка определяемые выражением:

                                                   (2.23)

Таким образом, уменьшение средней температуры описывается простым экспоненциальным законом. Для удобства прикидочных расчетов на рис. IV. 10 приведена номограмма зависимости между q и Fo.

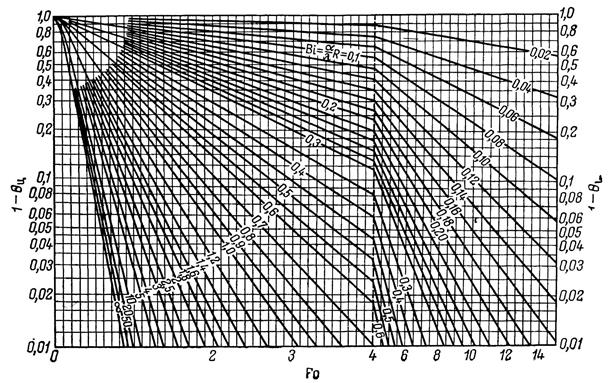
Рис. 2.5 Номограмма для определения зависимости между безразмерной средней избы­точной температурой и критерием Фурье в случае неограниченного цилиндра.