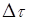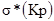В написанной программе формула (3.1) реализована через функцию:
Function Generator(m:Real;s:Real):Real;
Label L1;
BEGIN
L1:x:=0;
FOR i:=1 TO 12 DO
BEGIN
k:=Random;
x:=x+k;
END;
x:=x-6;
if (x>3) or (x<-3) then goto L1;
m:=m+s*x;
Generator:=m;
END ;
Таким образом, введя Generator(m,s)получим случайное число, распределенное по нормальному закону с параметрами m = m и s = s.
В соответствии с [1] формула получения случайных чисел, распределенных по равномерному закону с параметрами a и b следующая:
x = 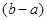 ×r+ a, (3.8)
×r+ a, (3.8)
где a, b – параметры равномерной модели;
r –стандартное равномерно распределенное случайное число в диапазоне 0..1.
В написанной программе формула (3.8) реализована через функцию:
Function Generator2(m:real;s:real):Real;
BEGIN
k:=Random;
m:=(s-m)*k+m;
Generator2:=m;
end;
Таким образом, введя Generator2(m, s)получим случайное число, распределенное по равномерному закону с параметрами a=m и b = s.
Пусть случайное число x, имеющее нормальное распределение с параметрами m = m(x) и s = s(x), уже получено. Тогда для получения случайного числа z, имеющего нормальное распределение с параметрами m = m(z) и s = s(z) и коррелированного с x, необходимо произвести смещение параметров m = m(z) и s = s(z) с учётом коэффициента парной корреляции, а затем воспользоваться подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x):
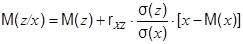 (3.9)
(3.9)
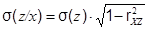 (3.10)
(3.10)
Определение величины смещения параметров m = M(z) и s = s(z) с учётом коэффициента парной корреляции в соответствии с формулами (3.9) и (3.10) в программе реализовано следующим образом:
Procedure Corr(x1,mx,mz,sx,sz:real; Var mzx,szx:real);
BEGIN
mzx:=mz+rxz*(sz/sx)*(x1-mx);
szx:=sz*sqrt(1-sqr(rxz));
END ;
Таким образом, введя Corr(x1,mx,mz,sx,sz,mzx,szx) получим случайное число, распределенное по нормальному закону с параметрами m = mzx и s = szx.
Обоснование выбора числа реализаций
Список идентификаторов
Список идентификаторов вычислительного алгоритма программы для ЭВМ.
Таблица 3.1
Обозначение параметра
Смысл параметра
| | В алгоритме
| В программе
|
| R1
| R1
| Сопротивление первого резистора
|
| R2
| R2
| Сопротивление второго резистора
|
| R3
| R3
| Сопротивление третьего резистора
|
| Rbx
| RW
| Входное сопротивление
|
| Koy
| KOU
| Коэффициент усиления
|
| SR1
| SR1
| Номинальное значение сопротивления 1-го резистора
|
| SR2
| SR2
| Номинальное значение сопротивления 2-го резистора
|
| SR3
| SR3
| Номинальное значение сопротивления 3-го резистора
|
| SKOU
| SKOU
| Номинальное значение коэффициента усиления
|
| SRW
| SRW
| Номинальное значение входного сопротивления
|
| Rtemp1
| Rtemp1
| Значения R1,учитывая температуру
|
| Rtemp2
| Rtemp2
| Значения R2,учитывая температуру
|
| Rtemp3
| Rtemp3
| Значения R3,учитывая температуру
|
| RWtemp
| RWtemp
| Значения RW,учитывая температуру
|
| KOUtemp
| KOUtemp
| Значения KOU,учитывая температуру
|
| Rtime1
| Rtime1
| Значения R1,учитывая старение
|
| Rtime2
| Rtime2
| Значения R2,учитывая старение
|
| Rtime3
| Rtime3
| Значения R3,учитывая старение
|
| RWtime
| RWtime
| Значения RW,учитывая старение
|
| KOUtime
| KOUtime
| Значения KOU,учитывая старение
|
| Kи
| Kideal
| Номинальное значение выходного параметра
|
| DKи
| dKideal
| Допуск на выходной параметр
|
| Kexit
| Kexit
| Значение выходного параметра n-смоделированного РЭУ
|
| aR+
| Rtpol
| Температурный коэффициент для R (+ обл.температур)
|
| aR-
| Rtotr
| Температурный коэффициент для R (- обл.температур)
|
| a Rbx
| RWt
| Температурный коэффициент для входного сопротивления
|
| a Koy
| KOUt
| Температурный коэффициент для коэффициента усиления
|
| СR
| Rct
| Коэффициент старения для резисторов
|
| С Rbx
| RWct
| Коэффициент старения для входного сопротивления
|
| С Koy
| KOUct
| Коэффициент старения для коэффициента усиления
|
| temp
| temp
| Равномерно распределенное значение температуры
|
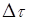
| time
| Заданное время работы
|
| -
| n
| Номер текущего смоделированного РЭУ
|
| N
| num
| Число реализаций РЭУ
|
| rxz
| rxz
| Коэффициент парной корреляции между RW и KOU
|
| -
| a,b
| Количество попаданий в ’’+’’-ю и ’’-’’-ю облсть температур
|
| Tv,Tn
| Tv,Tn
| Верхнее и нижнее значение диапазона рабочих температур
|
| -
| dR1..dR3,dRW,dKOU
| Производственный допуск на R1..R3 ,RW и KOU
|
| Р
| P,Р1, Р2
| Вероятности отсутствия параметрического отказа
|
| -
| mo1..mo3,mx,
mz,mzx
| Математические ожидания
|
| -
| s1..s3,sx,sz,szx
| Среднеквадратические отклонения
|
| М*(Kр)
| mo4
| Математическое ожидание выходного параметра
|
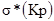
| s4
| Среднеквадратическое отклонение выходного параметра
|
| dx1…dx5
| dx1…dx5
| Сгенерированные значения температурных(временных) коэффициентов
|
| -
| x
| Стандартное нормально распределённое случайное число
|
| r(i)
| k
| Стандартное равномерно распределённое число в диапазоне (0…1)
|
| -
| sum…sum13
| Аккумуляторы суммы значений выходного параметра
|
 ×r+ a, (3.8)
×r+ a, (3.8)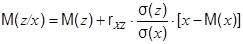 (3.9)
(3.9)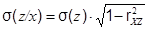 (3.10)
(3.10)