R1, R2, R3 - сопротивления 1-го, 2-го и 3-го резисторов;

Rbx - входное сопротивление, Koy - коэффициент усиления.

1. При помощи стандартной функции Random генерируем равномерно распределённое значение температуры: temp.

Здесь вычислительный алгоритм разделяется на 2 части:

а) Если температура попала в положительную область диапазона рабочих температур т.е 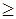 20 ,

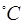то, используя формулу (3.1) [1] генерируем нормально распределённые значения температурных коэффициентов a_R+, a Rbx : dx1,dx2,dx3,dx 4.

a_R+ - температурный коэффициент для резисторов в полож-й области температур;

a Rbx - температурный коэффициент для входного сопротивления.

dx1, dx2, dx3, dx4 – сгенерированные значения температурных коэффициентов для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

б)Если температура попала в отрицательную область диапазона рабочих температур т.е 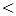 20 ,

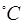то, используя формулу (3.1) [1] генерируем нормально распределённые значения температурных коэффициентов a_R+ , a Rbx : dx1,dx2,dx3,dx4.

a_R- - температурный коэффициент для резисторов в отриц-й области температур;

a Rbx - температурный коэффициент для входного сопротивления.

dx1, dx2, dx3, dx4 – сгенерированные значения температурных коэффициентов для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

x = s× 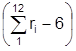+ m,          (3.1)

где x – нормально распределённое случайное число;

m – математическое ожидание;

s – среднеквадратичное отклонение;

r_i – стандартное равномерно распределенное случайное число в диапазоне 0..1. (r_i получаем при помощи стандартной функции Random).

Далее пересчитываем значения первичных параметров (R1,R2, R3, Rbx) с учётом воздействия температуры. Для этого воспользуемся формулами [1]:

           (3.2)

где 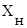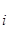– номинальные значения i-го первичного параметра;

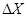
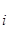–приращения значений i-го первичного параметра под действием температуры;

Согласно [1] относительное изменение i-го первичного параметра под воздействием температуры (старения) можно выразить следующим образом:

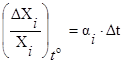         (3.3)

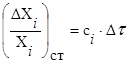        (3.4)

где 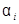– температурный коэффициент i-го первичного параметра;

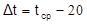°C,

где t_ср – температура окружающей среды;

с_i – коэффициент старения i-го первичного параметра;

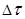– рассматриваемый интервал времени.

В качестве t_ср для положительной области диапазона рабочих температур примем

наибольшую из возможных температур - Tv, а для отрицательной области примем наименьшую из возможных температур - Tn. С учётом этого и формул (3.3) и (3.4) формула (3.2) примет вид:

для ‘‘+‘‘ -ой области температур:

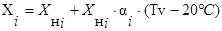 (3.5)

С учётом этой формулы получаем:

; ; ; ;

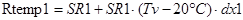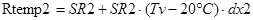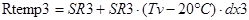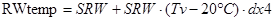для ‘‘-‘‘ -ой области температур:

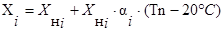 (3.6)

С учётом этой формулы получаем:

; ;

; ;

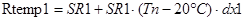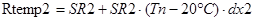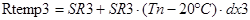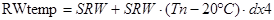где Rtemp1, Rtemp2, Rtemp3 - значения сопротивлений 1-го, 2-го и 3-го резисторов соответственно с учётом действия температуры.

RWtemp – значение входного сопротивления под действием температуры.

SR1, SR2, SR3 – номинальные значения 1-го, 2-го и 3-го резисторов соответственно.

SRW – номинальное значение входного сопротивления.

Для получения значений коэффициента усиления (Koy) производим смещение параметров m = m(z) и s = s(z) его температурного коэффициента (a Koy) с учётом коэффициента парной корреляции 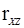, а затем, воспользовавшись подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x) генерируем нормально распределённое значение его температурного коэффициента(a Koy):dx5.

dx5 - сгенерированное значение температурного коэффициента для коэффициента усиления.

Воспользовавшись формулой (3.5) (для положительной области температур) или (3.6) (для отрицательной области температур) пересчитываем значения коэффициента усиления (Koy) с учётом воздействия температуры:

для ‘‘+‘‘ -ой области температур:

;

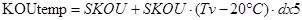для ‘‘-‘‘ -ой области температур: ;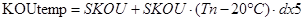

где KOUtemp – значение коэффициента усиления под действием температуры.

SKOU – номинальное значение коэффициента усиления.

В отрицательной и положительной области температур по формуле (1.1) определяем значение выходного параметра - коэффициента передачи (Kexit).

2. Используя формулу (3.1) генерируем нормально распределённые значения коэффициентов старения С_R, С Rbx :dx1,dx2,dx3,dx4.

С_R – коэффициент старения для резисторов;

С Rbx – коэффициент старения для входного сопротивления;

dx1, dx2, dx3, dx4 – сгенерированные значения коэффициентов старения для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

Воспользовавшись формулой:

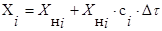 (3.7)

пересчитываем значения первичных параметров (R1,R2, R3, Rbx) с учётом воздействия старения:

; ;

; ;

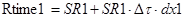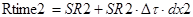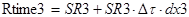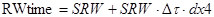где Rtime1, Rtime2, Rtime3 - значения сопротивлений 1-го, 2-го и 3-го резисторов соответственно с учётом действия старения.

RWtime – значение входного сопротивления под действием старения.

SR1, SR2, SR3 – номинальные значения 1-го, 2-го и 3-го резисторов соответственно.

SRW – номинальное значение входного сопротивления.

Для получения значений коэффициента усиления (Koy) производим смещение параметров m = m(z) и s = s(z) его коэффициента старения(С Koy) с учётом коэффициента парной корреляции 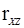, а затем, воспользовавшись подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x) генерируем нормально распределённое значение его коэффициента старения(С Koy):dx5.

Воспользовавшись формулой (3.7) пересчитываем значения коэффициента усиления (Koy) с учётом воздействия старения:

;

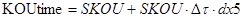где KOUtime – значение коэффициента усиления под действием температуры.

SKOU – номинальное значение коэффициента усиления.

По формуле (1.1) определяем значение выходного параметра: коэффициента передачи (Kexit).