Кафедра: радиоэлектронных средств
Пояснительная записка к курсовому проекту
по предмету: «Теоретические основы конструирования, технологии и надежности»
на тему: «Оценка параметрической надежности РЭС с использованием моделирования на ЭВМ постепенных отказов»
Москва 2002
СОДЕРЖАНИЕ
Введение
1. Постановка задачи
1.1 Анализ исходных данных
1.2 Пояснение решаемой задачи
2. Выбор метода решения поставленной задачи
3. Решение задачи на ЭВМ
3.1 Описание вычислительного алгоритма моделирования температурных и временных изменений параметров.
3.2 Пояснение процедур и функций, используемых в программе
3.3 Обоснование выбора числа реализаций
3.4 Список идентификаторов
4. Описание и анализ полученных результатов
5. Пояснения функциональных частей структурной схемы алгоритма
Заключение и выводы.
Литература.
Приложение 1. Листинг программы.
Приложение 2. Графический материал.
ВВЕДЕНИЕ
В курсовом проекте необходимо произвести оценку параметрической надёжности РЭС, с использованием моделирования на ЭВМ постепенных отказов элементов.
Параметрическая надёжность РЭУ - вероятность отсутствия в изделии постепенных отказов при его работе в заданных условиях эксплуатации в течение времени tзад (в нашем случае tзад = 10000 ч). Параметрическая надёжность связана с понятием постепенных отказов.
Постепенный (параметрический) отказ - отказ, возникающий в результате постепенного изменения значения одного или нескольких параметров изделия.
Основные причины, вызывающие появление постепенных отказов:
1) Производственный разброс выходного параметра, вызываемый действием производственных погрешностей.
2) Отклонение выходного параметра от номинального значения из-за процессов старения.
3) Отклонение выходного параметра от номинального значения под воздействием дестабилизирующих факторов (температуры, влажности и т.д.).
Из-за наличия производственного разброса входных параметров выходной параметр уже может существенно отклониться от номинального значения. Под воздействием дестабилизирующих факторов на первичные параметры, а также в процессе эксплуатации происходит дальнейшее изменение выходного параметра. В результате его значение может достигнуть критического значения и выйти за него, т.е наступит постепенный отказ.
Моделируя РЭУ и используя методы математической статистики, проследим как влияют производственный разброс входных параметров, дестабилизирующие факторы и старение на выходной параметр, а следовательно и на параметрическую надежность.
ПОСТАНОВКА ЗАДАЧИ
Анализ исходных данных
Исходные данные к проекту:
1) Схема электрическая принципиальная.
2) Математическая модель для выходного параметра:
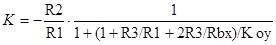(1.1)
3) Сведения о первичных параметрах (параметрах элементов):
а) резисторы R1 = 3 кОм ± 5% типа ОМЛТ;
б) резисторы R2 = 12 кОм ± 5% типа ОМЛТ;
в) резисторы R3 = 2,4 кОм ± 10% типа ОМЛТ;
г) тип микросхемы DA1: 140УД9;
4) Заданное интервал работы РЭС: tзад = 10000 час.
5) Диапазон рабочих температур: Траб = +10°…+60° С.
6) Условие параметрической надежности:
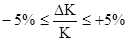
Данных, указанных в задании, недостаточно для проведения расчетов и моделирования. Поэтому дополняем необходимые данные из справочников:
7) Согласно [3] температурный коэффициент резисторов типа ОМЛТ:
а) aR+ = ±7×10-2 %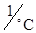 
при Т = +20°…+100° С;
б) aR- = ±12×10-2 % 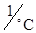при Т = -60°… +20° С;
8) Согласно [3] на резисторы типа ОМЛТ величина их сопротивления может измениться на ± 10% при наработке 25000 часов. Отсюда находим величину коэффициента старения:
СR =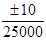 
= ± 4×10-4 % 
;
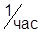9) Согласно [2] коэффициент усиления Koy и входное сопротивлениеRbx:
Koy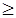 
35000
Rbx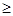 
300 кОм
Характеристики первичных параметров представлены в неявной форме, т. е. нет численных значений математического ожидания М(xi) и среднеквадратического отклонения s(xi).Вследствие этого необходимо произвести их расчет.
Расчет этих характеристик производят в зависимости от закона распределения первичного параметра. Примем гипотезу о том, что Koy и Rbx распределены по нормальному закону. w(Koy)
 |
35000 М(Koy) Koy
Согласно [1] составим систему уравнений:
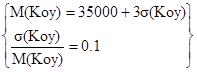
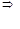
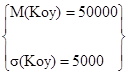
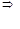Koy=50000±30%
Аналогично определяем Rbx .Получаем Rbx=430 кОм±30%.
Т.о. получили Koy=50000±30% Rbx=430 кОм±30%
10) На основе данных, приведённых в [2] получили стабильность Koy и Rbx :
а)Температурная : a Koy= ±25×10-2 %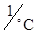 
при Т = -60°…+100° С;
a Rbx = ±7,5×10-3 %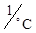 
при Т = -60°…+100° С;
б)Временная: С Koy= ±3×10-3%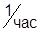 
; С Rbx= ±5×10-4 % 
;
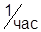11) Коэффициент корреляции между Koy и Rbx: r =0.8
Пояснение решаемой задачи
В курсовом проекте необходимо произвести оценку параметрической надёжности РЭС, с использованием моделирования на ЭВМ постепенных отказов элементов.
Оценка параметрической надёжности - определение основных количественных показателей сохранения рабочих функций при возможных постепенных изменениях параметров комплектующих элементов в условиях эксплуатации.
Оценку параметрической надежности будем проводить следующим способом: Подсчитав по формуле (1.1) выходной параметр K (коэффициент передачи) и установив допуск на выходной параметр DK, смоделируем n РЭУ. РЭУ будем считать работоспособным, если значение коэффициента передачи лежит в диапазоне установленного допуска, т.е. K ± DK. Таким образом, найдём вероятность отсутствия параметрического отказа (см. раздел 2).
РЕШЕНИЕ ЗАДАЧИ НА ЭВМ
BEGIN
L1:x:=0;
FOR i:=1 TO 12 DO
BEGIN
k:=Random;
x:=x+k;
END;
x:=x-6;
if (x>3) or (x<-3) then goto L1;
m:=m+s*x;
Generator:=m;
END ;
Таким образом, введя Generator(m,s)получим случайное число, распределенное по нормальному закону с параметрами m = m и s = s.
В соответствии с [1] формула получения случайных чисел, распределенных по равномерному закону с параметрами a и b следующая:
x =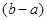 
×r+ a, (3.8)
где a, b – параметры равномерной модели;
r –стандартное равномерно распределенное случайное число в диапазоне 0..1.
В написанной программе формула (3.8) реализована через функцию:
Function Generator2(m:real;s:real):Real;
BEGIN
k:=Random;
m:=(s-m)*k+m;
Generator2:=m;
end;
Таким образом, введя Generator2(m, s)получим случайное число, распределенное по равномерному закону с параметрами a=m и b = s.
Пусть случайное число x, имеющее нормальное распределение с параметрами m = m(x) и s = s(x), уже получено. Тогда для получения случайного числа z, имеющего нормальное распределение с параметрами m = m(z) и s = s(z) и коррелированного с x, необходимо произвести смещение параметров m = m(z) и s = s(z) с учётом коэффициента парной корреляции, а затем воспользоваться подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x):
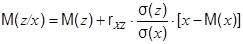(3.9)
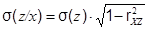(3.10)
Определение величины смещения параметров m = M(z) и s = s(z) с учётом коэффициента парной корреляции в соответствии с формулами (3.9) и (3.10) в программе реализовано следующим образом:
Procedure Corr(x1,mx,mz,sx,sz:real; Var mzx,szx:real);
BEGIN
mzx:=mz+rxz*(sz/sx)*(x1-mx);
szx:=sz*sqrt(1-sqr(rxz));
END ;
Таким образом, введя Corr(x1,mx,mz,sx,sz,mzx,szx) получим случайное число, распределенное по нормальному закону с параметрами m = mzx и s = szx.
Список идентификаторов
Список идентификаторов вычислительного алгоритма программы для ЭВМ.
Таблица 3.1
Обозначение параметра
Смысл параметра
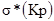
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
В результате проделанной работы было выявлено:
1) На параметрическую надежность РЭУ в большей степени влияет производственный допуск на параметры элементов РЭУ, тогда как дестабилизирующий фактор (температура) и процессы старения (при данных температурных коэффициентах и коэффициентах старения при заданном времени tзад = 10000 час) влияют в меньшей степени, однако уменьшают вероятность, с которой гарантируется отсутствие постепенного отказа.
2) Опыт эксплуатации РЭУ показывает, что эксплуатационная надёжность практически всегда ниже того уровня, который получается по результатам расчёта. Это объясняется как несовершенством технологии производства, так и низкой достоверностью справочной информации.
ЛИТЕРАТУРА
1. Боровиков С.М. Теоретические основы конструирования, технологии и надежности, -- Минск: Дизайн - Про, 1998.
2. Богданович М.И , Грель И.Н Интегральные микросхемы. Справочник, - Минск.: Полымя,1996
3. Папиев В.П. Сопротивления (том1),Справочник--М.: Электростандарт, 1977.
4. Фомин А.В., Борисов В.Ф., Чермошенский В.В. Допуски в радиоэлектронной аппаратуре, - М.: Советское радио, 1973.
5. Теоретические основы конструирования, технологии и надежности. Методические указания к курсовой работе под ред. Боровикова С.М., - Минск: БГУИР, 1995.
6. ГОСТ 19.002-80 Схемы алгоритмов и программ. Правила выполнения.
7. ГОСТ 2.105-95 Общие требования к текстовым документам.
ПРИЛОЖЕНИЕ 1
ЛИСТИНГ ПРОГРАММЫ
PROGRAM Toktin;USES Crt;Label L1;VAR k,x,x1,R1,R2,R3,RW,KOU,Kexit,sum,sum1,sum2,sum3,sum4,sum5,sum6,sum7,sum8,sum9,sum10,sum11,sum12,sum13,mo1,mo2,mo3,mo4,s1,s2,s3,s4,mx,mz,mzx,sx,sz,szx,rxz,P1,P2,P,SR1,SR2,SR3,SRW,SKOU,dR1,dR2,dR3,dR4,dRW,dKOU,Kideal,dKideal,Rtotr,Rtpol,Rct,RWt,KOUt,RWct,KOUct,Rtemp1,Rtemp2,Rtemp3,Rtemp4,RWtemp,KOUtemp,Rtime1,Rtime2,Rtime3,Rtime4,RWtime,KOUtime,temp,dx1,dx2,dx3,dx4,dx5,Tn,Tv:Real;i,a,b:Integer;time,num,n:Integer;Function Generator(m:Real;s:Real):Real;Label L1;BEGINL1:x:=0;FOR i:=1 TO 12 DOBEGINk:=Random;x:=x+k;END;x:=x-6;if (x>3) or (x<-3) then goto L1;m:=m+s*x;Generator:=m;END;Function Generator2(m:real;s:real):Real;BEGINk:=Random;m:=(s-m)*k+m;Generator2:=m;end;Procedure Corr(x1,mx,mz,sx,sz:real; Var mzx,szx:real);BEGINmzx:=mz+rxz*(sz/sx)*(x1-mx);szx:=sz*sqrt(1-sqr(rxz));END;BEGIN textbackground(1);ClrScr;Randomize;TextColor(10);GotoXY(12,2);Writeln('ОЦЕHКА ПАРАМЕТРИЧЕСКОЙ HАДЕЖHОСТИ РЭС');GotoXY(3,3);Writeln('С ИСПОЛЬЗОВАHИЕМ МОДЕЛИРОВАHИЯ HА ЭВМ ОТКАЗОВ ЭЛЕМЕHТОВ');GotoXY(1,4);
Writeln('------------------------------------------------------------');Writeln(' Исходные данные: ');Writeln(' -принципиальная схема ');Writeln(' -тип резисторов ОМЛТ ');Writeln(' -тип аналоговой микросхемы DA1:140УД9 ');Writeln(' Факторы принимаемые во внимание: ');Writeln(' -температура (диапазон +10..+60C) ');Writeln(' -старение (Tз=10000 часов) ');riteln('------------------------------------------------------------');Writeln(' Программа будет моделировать постепенные отказы элементов ');Writeln(' и рассчитывать вероятность, с которой гарантируется ');Writeln(' отсутствие постепенного отказа при заданных условиях. ');Writeln('------------------------------------------------------------');ReadKey;ClrScr;Writeln('------------------------------------------------------------');Writeln(' Ввод необходимых данных для рассчета: ');Write(' -введите номинал R1 (рекомендуется 3000.Om +/-5%): ');Read(SR1);GotoXY(63,3);Write('+/-');GotoXY(67,3); Readln(dR1);Write(' -введите номинал R2 (рекомендуется 12000.Om+/-5%): ');Read(SR2);GotoXY(63,4);Write('+/-');GotoXY(67,4); Readln(dR2);Write(' -введите номинал R3(рекомендуется 2400.Om +/-10%): ');Read(SR3);GotoXY(63,5);Write('+/-');GotoXY(68,5);Readln(dR3);Write (' -введите вх.сопротивление RW(рекомендуется 430000.Om+/-30%): ');Read(SRW);GotoXY(70,6);Write('+/-');GotoXY(73,6);Readln(dRW);Write (' -введите коэф-т усиления О.У. KOU (рекомендуется 50000+/-30%): ');Read(SKOU);GotoXY(72,7);Write('+/-');GotoXY(76,7);Readln(dKOU);Writeln(' -введите температурные коэффициенты :');Write (' для R, T=-60..+20C (рекомендуется +/-0.12%): ');Readln(Rtotr);rite (' для R, T=+20..+100C (рекомендуется +/-0.07%): ');Readln(Rtpol);Write (' для RW, T=-60..+100C (рекомендуется +/-0.0075%): ');Readln(RWt);Write (' для KOU, T=-60..+100C (рекомендуется +/-0.25%): ');Readln(KOUt);Writeln(' -введите коэффициенты старения:');Write (' для R (рекомендуется +/-0.0004%) :');Readln(Rct);Write (' для RW (рекомендуется +/-0.0005) :');Readln(RWct);Write (' для KOU (рекомендуется +/-0.003) :');Readln(KOUct);rite(' -введите коэффициент парной корреляции между KOU и RW:');Readln(rxz);Kideal:=(-SR2/SR1)*(1/(1+(1+SR3/SR1+2*SR3/SRW)/SKOU));WriteLn('Коэффициент передачи Kideal=',Kideal:4:3);Write(' -условие отсутствия постепенного отказа в %: ');ReadLn(dKideal);Write (' -количество модулируемых экземпляров: ');Readln(num);Write (' -заданное время работы Тз: ');Readln(time);writeln ('Введите заданный диапазон рабочих температур: '); writeln;write ('Нижняя граница температурного диапазона : '); read(Tn);
write ('Верхняя граница температурного диапазона : '); read(Tv);Writeln(' -----------------------------------------------------------');Writeln(' Моделирование и рассчет займут некоторое время. ');Readkey;TextColor(13+Blink);Writeln(' ПРОИЗВОДИТСЯ МОДЕЛИРОВАHИЕ И РАССЧЕТ: ');TextColor(15);
sum:=0;sum1:=0;sum2:=0;sum3:=0;sum4:=0;sum5:=0;sum6:=0;sum7:=0;
sum8:=0;sum9:=0; sum10:=0;sum11:=0;sum12:=0;sum13:=0;FOR n:=1 TO num DOBEGINif dR1<=5 thenR1:=Generator2(SR1-(SR1*dR1/100),SR1+(SR1*dR1/100))elseR1:=Generator(SR1,(SR1*dR1/300));if dR2<=5 thenR2:=Generator2(SR2-(SR2*dR2/100),SR2+(SR2*dR2/100))elseR2:=Generator(SR1,(SR1*dR1/300));if dR3<=5 thenR3:=Generator2(SR3-(SR3*dR3/100),SR3+(SR3*dR3/100))elseR3:=Generator(SR3,(SR3*dR3/300));RW:=Generator(SRW,(SRW*dRW/300));Corr(RW,SRW,SKOU,(SRW*dRW/300),(SKOU*dKOU/300),mzx,szx);KOU:=Generator(mzx,szx);Kexit:=(-R2/R1)*(1/(1+(1+R3/R1+2*R3/RW)/KOU));sum:=sum+(Kexit);sum1:=sum1+sqr(Kexit);temp:=Generator2(Tn,Tv);if (temp>=20) thenbegina:=a+1;dx1:=Generator(0,(Rtpol/300));R1:=R1+R1*Abs(20-Tv)*dx1;Rtemp1:=SR1+SR1*Abs(20-Tv)*dx1;dx2:=Generator(0,(Rtpol/300));R2:=R2+R2*Abs(20-Tv)*dx2;Rtemp2:=SR2+SR2*Abs(20-Tv)*dx2;dx3:=Generator(0,(Rtpol/300));R3:=R3+R3*Abs(20-Tv)*dx3;Rtemp3:=SR3+SR3*Abs(20-Tv)*dx3;dx4:=Generator(0,RWt/300);RW:=RW+RW*Abs(20-Tv)*dx4;RWtemp:=SRW+SRW*Abs(20-Tv)*dx4;Corr(dx4,0,0,RWt/300,KOUt/300,mzx,szx);dx5:=Generator(mzx,szx);KOU:=KOU+KOU*Abs(20-Tv)*dx5;KOUtemp:=SKOU+SKOU*Abs(20-Tv)*dx5;Kexit:=(-Rtemp2/Rtemp1)*(1/(1+(1+Rtemp3/Rtemp1+2*Rtemp3/RWtemp)/KOUtemp));sum2:=sum2+(Kexit);sum3:=sum3+sqr(Kexit);dx1:=Generator(0,(Rct/300));R1:=R1+R1*time*dx1;Rtime1:=SR1+SR1*time*dx1;dx2:=Generator(0,(Rct/300));R2:=R2+R2*time*dx2;Rtime2:=SR2+SR2*time*dx2;dx3:=Generator(0,(Rct/300));R3:=R3+R3*time*dx3;Rtime3:=SR3+SR3*time*dx3;dx4:=Generator(0,(Rct/300));RW:=RW+RW*time*dx4;RWtime:=SRW+SRW*time*dx4;Corr(dx4,0,0,RWct/300,KOUct/300,mzx,szx);dx5:=Generator(mzx,szx);KOU:=KOU+KOU*time*dx5;KOUtime:=SKOU+SKOU*time*dx5;Kexit:=(-Rtime2/Rtime1)*(1/(1+(1+Rtime3/Rtime1+2*Rtime3/RWtime)/KOUtime));sum4:=sum4+(Kexit); sum5:=sum5+sqr(Kexit);Kexit:=(-R2/R1)*(1/(1+(1+R3/R1+2*R3/RW)/KOU));sum6:=sum6+(Kexit);sum7:=sum7+sqr(Kexit);IF Kexit<(Kideal-Kideal*dKideal/100) THENIF Kexit>(Kideal+Kideal*dKideal/100) THEN P1:=P1+1;end;if (temp<20) thenbeginb:=b+1;dx1:=Generator(0,(Rtotr/300));R1:=R1+R1*Abs(20-Tn)*dx1;Rtemp1:=SR1+SR1*Abs(20-Tn)*dx1;dx2:=Generator(0,(Rtotr/300));R2:=R2+R2*Abs(20-Tn)*dx2;Rtemp2:=SR2+SR2*Abs(20-Tn)*dx2;dx3:=Generator(0,(Rtotr/300));R3:=R3+R3*Abs(20-Tn)*dx3;Rtemp3:=SR3+SR3*Abs(20-Tn)*dx3;dx4:=Generator(0,RWt/300);RW:=RW+RW*Abs(20-Tn)*dx4;RWtemp:=SRW+SRW*Abs(20-Tn)*dx4;Corr(dx4,0,0,RWt/300,KOUt/300,mzx,szx);dx5:=Generator(mzx,szx);KOU:=KOU+KOU*Abs(20-Tn)*dx5;KOUtemp:=SKOU+SKOU*Abs(20-Tn)*dx5;Kexit:=(-temp2/Rtemp1)*(1/(1+(1+Rtemp3/Rtemp1+2*Rtemp3/RWtemp)/KOUtemp));sum8:=sum8+(Kexit); sum9:=sum9+sqr(Kexit);dx1:=Generator(0,(Rct/300));R1:=R1+R1*time*dx1;Rtime1:=SR1+SR1*time*dx1;dx2:=Generator(0,(Rct/300));R2:=R2+R2*time*dx2;Rtime2:=SR2+SR2*time*dx2;dx3:=Generator(0,(Rct/300));R3:=R3+R3*time*dx3;Rtime3:=SR3+SR3*time*dx3;dx4:=Generator(0,RWct/300);RW:=RW+RW*time*dx4;RWtime:=SRW+SRW*time*dx4;Corr(dx4,0,0,RWct/300,KOUct/300,mzx,szx);dx5:=Generator(mzx,szx);KOU:=KOU+KOU*time*dx5;KOUtime:=SKOU+SKOU*time*dx5;Kexit:=(-Rtime2/Rtime1)*(1/(1+(1+Rtime3/Rtime1+2*Rtime3/RWtime)/KOUtime));sum10:=sum10+(Kexit); sum11:=sum11+sqr(Kexit);Kexit:=(-R2/R1)*(1/(1+(1+R3/R1+2*R3/RW)/KOU));sum12:=sum12+(Kexit); sum13:=sum13+sqr(Kexit);IF Kexit<(Kideal-Kideal*dKideal/100) THENIF Kexit>(Kideal+Kideal*dKideal/100) THEN P2:=P2+1;end;END;P1:=P1/a;P2:=P2/b;IF P2>P1 thenbegin P:=P1;mo1:=sum/num;mo2:=sum2/a;mo3:=sum4/a;mo4:=sum6/a;s1:=sqrt((sum1-sqr(sum)/num)/(num-1));s2:=sqrt((sum3-sqr(sum2)/a)/(a-1));s3:=sqrt((sum5-sqr(sum4)/a)/(a-1));s4:=sqrt((sum7-sqr(sum6)/a)/(a-1));end;if P2<P1 thenbeginP:=P2;mo1:=sum/num;mo2:=sum8/b;mo3:=sum10/b;mo4:=sum12/b;s1:=sqrt((sum1-sqr(sum)/num)/(num-1));s2:=sqrt((sum9-sqr(sum8)/b)/(b-1));s3:=sqrt((sum11-sqr(sum10)/b)/(b-1));s4:=sqrt((sum13-sqr(sum12)/b)/(b-1));end;
ClrScr;WriteLn('Коэффициент передачи: ',Kideal:6:3);WriteLn('Математическое ожидание, учитывая производственный допуск:',mo1:6:3);WriteLn('Среднеквадратичное отклоненение: ',s1:6:4);WriteLn('Математическое ожидание, учитывая температурный допуск: ' ,mo2:6:3);WriteLn('Среднеквадратичное отклоненение: ',s2:6:4);WriteLn('Математическое ожидание, учитывая старение: ',mo3:6:3);WriteLn('Среднеквадратичное отклоненение: ',s3:6:4);WriteLn('Математическое ожидание, учитывая все факторы: ',mo4:6:3);WriteLn('Среднеквадратичное отклоненение: ',s4:6:4);Writeln('-------------------------------------------------------------------------');WriteLn('Вероятность отсутствия параметрического отказа: ');WriteLn('P=',P:6:4);if num<4*Sqr(s4)/Sqr(0.01) thenBeginwriteln('Не достигнута заданная точность !');writeln('Следует сделать число реализаций процесса сделать>',num,'!');end;REPEAT UNTIL KeyPressed;END.
Кафедра: радиоэлектронных средств
Дата: 2019-07-30, просмотров: 183.
