Месячная производительность труда одного рабочего
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒
Поможем в ✍️ написании учебной работы
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

 

Месячная производительность труда одного рабочего по всей совокупности предприятий рассчитывается по формуле:

 

 

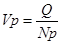
Q- Объем товарной продукции,

Np- Среднесписочная численность рабочих.

Таблица 1.3

№ Объем товарной продукции, млн. р. Среднесписочная численность рабочих, чел. Месячная производительность труда одного рабочего, тыс. р/чел.
1 163,8 205 0,0000665854
2 236,5 267 0,0000738140
3 843,3 668 0,0001052021
4 1005,9 714 0,0001174020
5 696,3 544 0,0001066636
6 1031,3 622 0,0001381699
7 1361,2 683 0,0001660810
8 1712,9 728 0,0001960737
9 538,9 526 0,0000853771
10 350,4 267 0,0001093633
11 2149,9 868 0,0002064036
12 352,8 228 0,0001289474
13 1187,1 718 0,0001377786
14 262,4 270 0,0000809877
15 438,8 413 0,0000885391
16 1150,5 695 0,0001379496
17 249,4 364 0,0000570971
18 655,3 595 0,0000917787
19 2549,5 914 0,0002324489
20 536,8 320 0,0001397917
21 311,2 256 0,0001013021
22 809,7 570 0,0001183772
23 166,7 229 0,0000606623
24 2185,1 879 0,0002071578
25 2066,2 798 0,0002157686

 



Средние показатели

 

Средние показатели по всей совокупности предприятий рассчитываются по следующим формулам:

 

; ; ; .

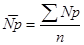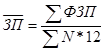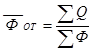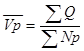Таблица 2.1

№ Среднеспи-сочная численность рабочих, чел. Среднемесячная заработная плата работника, тыс. р/мес. Фондоотдача основных фондов Среднемесячная производительность труда одного рабочего, тыс. р/чел.
1 205 13,65854 0,909495 0,0000665854
2 267 19,72534 0,803056 0,0000738140
3 668 30,06487 2,00404 0,0001052021
4 714 32,13119 2,14158 0,0001174020
5 544 24,46385 1,631061 0,0001066636
6 622 28,00107 1,866944 0,0001381699
7 683 30,7223 2,048149 0,0001660810
8 728 32,77244 2,184264 0,0001960737
9 526 23,65336 1,576653 0,0000853771
10 267 29,15106 0,8 0,0001093633
11 868 39,0649 2,604677 0,0002064036
12 228 29,45906 1,96218 0,0001289474
13 718 32,28877 2,152493 0,0001377786
14 270 21,88272 0,811379 0,0000809877
15 413 18,56336 1,238848 0,0000885391
16 695 31,27098 2,084617 0,0001379496
17 364 16,39194 1,092422 0,0000570971
18 595 26,7507 1,783615 0,0000917787
19 914 41,1105 2,740514 0,0002324489
20 320 31,38021 2,988864 0,0001397917
21 256 25,94401 0,768775 0,0001013021
22 570 25,65789 1,710754 0,0001183772
23 229 13,86463 0,924058 0,0000606623
24 879 39,57148 2,638054 0,0002071578
25 798 35,9127 2,394761 0,0002157686
Среднее 533,64 30,236364 1,947784 0,143742

 

 



Группировка статистических данных

Простая аналитическая группировка

 

Величина равных интервалов определяется по формуле:

 

 

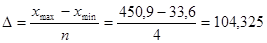
где 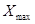и 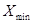 - максимальное и минимальное значение признака;

n - заданное количество интервалов группировки

Анализ данных таблицы 3.1 показывает, что самое большое количество предприятий находится в первой группе, а наименьшее в четвертой. Фондоотдача основных фондов, среднесписочная численность рабочих и среднемесячная заработная плата работника предприятия находятся в прямой зависимости от фонда заработной платы.

 

Комбинационная группировка

 

Согласно исходным данным группировочные признаки: фонд заработной платы и фондоотдача основных фондов, а результативными являются среднесписочная численность рабочих, производительность труда одного рабочего.

∆1=104,325

 

∆2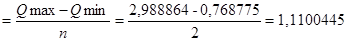

 



Таблица 3.2

Номер

групппы

Группы фирм

Номера фирм

Среднесписочная численность рабочих, чел.

Производительность труда одного рабочего, р/чел.
По Фонду заработной платы, тыс.р.

По фондоотдаче основных фондов

 Суммарная Средняя Суммарная Средняя

I

33,6-137,925

0,768775-1,8788195

 1,2,10, 14,15, 17,21,23 2271 283,875 0,0006383509 0,0000797939

1,8788195-2,988864

 12,20 548 274 0,0002687390 0,0001343695

Итого:

 10 2819 281,9 0,0009070899 0,00009070899

II

137,925-242,25

 0,768775-1,8788195 5,6,9,18, 22 2857 571,4 0,0005403664 0,000108073
1,8788195-2,988864 3 668 668 0,0001052021 0,0001052021

Итого:

 6 3525 587,5 0,0006455685 0,000107595

III

242,25- 346,575

 0,768775-1,8788195 0 0 0 0 0
1,8788195-2,988864 4,7,8,13,16,25 4336 722,66666 0,0009710535 0,000161842

Итого:

 6 4336 722,66666 0,0009710535 0,000161842

IV

346,575-450,9

 0,768775-1,8788195 0 0 0 0 0
1,8788195-2,988864 11,19,24 2661 887 0,0006460103 0,000215337

Итого:

 3 2661 887 0,0006460103 0,000215337
                 

Наибольшее количество предприятий состоит в первой группе, наибольшая производительность труда одного рабочего у предприятий входящих в 4 группу, а так же в этой группе наибольшие показатели среднесписочной численности рабочих. Среднесписочная численность рабочих и производительность труда одного рабочего находятся в прямой зависимости с фондом заработной платы и фондоотдачей основных фондов.



Проверка статистической совокупности на однородность

 

В своей работе проверку статистической совокупности на однородность я произвожу с использованием коэффициента вариации по признаку Фонд заработной платы.

 

Таблица 4.1

ФЗП(Xi)

Xi-X

(Xi-X)^2
33,6

-160,024

25607,68
63,2

-130,424

17010,42
241

47,376

2244,485
275,3

81,676

6670,969
159,7

-33,924

1150,838
209

15,376

236,4214
251,8

58,176

3384,447
286,3

92,676

8588,841
149,3

-44,324

1964,617
93,4

-100,224

10044,85
406,9

213,276

45486,65
80,6

-113,024

12774,42
278,2

84,576

7153,1
70,9

-122,724

15061,18
92

-101,624

10327,44
260,8

67,176

4512,615
71,6

-122,024

14889,86
191

-2,624

6,885376
450,9

257,276

66190,94
120,5

-73,124

5347,119
79,7

-113,924

12978,68
175,5

-18,124

328,4794
38,1

-155,524

24187,71
417,4

223,776

50075,7
343,9

150,276

22582,88

4840,6

0

368807,2

 

Среднее линейное отклонение – это среднее значение отклонений вариантов признака от их средней величины:

X=193,624

 

,

 

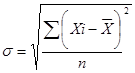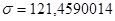
xi – варианты признака

х – средняя величина признака

n – численность единиц совокупности

 

 

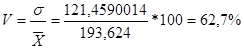
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.

Далее я рассчитываю коэффициенты вариации для простой группировки.

Для первой группы:

Таблица 4.2

Xi

Xi-X10

(Xi-X)^2
33,6

-40,76

1661,378
63,2

-11,16

124,5456
93,4

19,04

362,5216
80,6

6,24

38,9376
70,9

-3,46

11,9716
92

17,64

311,1696
71,6

-2,76

7,6176
120,5

46,14

2128,9
79,7

5,34

28,5156
38,1

-36,26

1314,788

743 ,6

0

5990,344


X=74,36

σ=24,47518

 

 

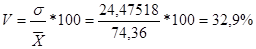
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.

Нужно произвести перегруппировку.

 

Для второй группы:


Таблица 4.3

Xi

Xi-X6

(Xi-X)^2
241

53,4167

2853,34
159,7

-27,8833

777,4803
209

21,4167

458,6736
149,3

-38,2833

1465,614
191

3,41667

11,67361
175,5

-12,0833

146,0069

1125,5

0

5712,788

 

X=187,5833

σ=30,85663

 

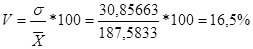
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

Для третьей группы:


Таблица 4.4

Xi

Xi-X6

(Xi-X)^2
275,3

-7,41667

55,00694
251,8

-30,9167

955,8403
286,3

3,583333

12,84028
278,2

-4,51667

20,40028
260,8

-21,9167

480,3403
343,9

61,18333

3743,4

1696,3

0

5267,828

X=282,7167

σ=29,63058

 

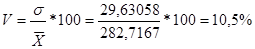
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

 

Для четвертой группы:

Таблица 4.5

Xi

Xi-X

(Xi-X)^2
406,9

-18,1667

330,0278
450,9

25,83333

667,3611
417,4

-7,66667

58,77778

1275,2

0

1056,167

X=425,0667

σ=13,26755

 

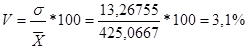
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.



Дата: 2019-07-30, просмотров: 245.

⇐ Предыдущая1234Следующая ⇒
fb
inst
tw
vk
Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024