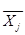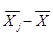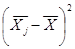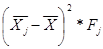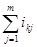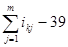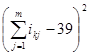Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Среднемесячная заработная плата работника предприятия

 

Среднемесячная заработная плата рабочего по всей совокупности предприятий рассчитывается по формуле:

 

 

 

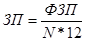
ФЗП- Фонд заработной платы (без учета выплат в различные фонды),

N- Среднесписочная численность работающих, чел.

Таблица 1.1

№	Фонд заработной платы (без учета выплат в различные фонды), млн р	Среднесписочная числен-ность работающих, чел.	Среднемесячная заработная плата работника предприятия, тыс. р/мес.
1	33,6	205	13,65854
2	63,2	267	19,72534
3	241,0	668	30,06487
4	275,3	714	32,13119
5	159,7	544	24,46385
6	209,0	622	28,00107
7	251,8	683	30,7223
8	286,3	728	32,77244
9	149,3	526	23,65336
10	93,4	267	29,15106
11	406,9	868	39,0649
12	80,6	228	29,45906
13	278,2	718	32,28877
14	70,9	270	21,88272
15	92,0	413	18,56336
16	260,8	695	31,27098
17	71,6	364	16,39194
18	191,0	595	26,7507
19	450,9	914	41,1105
20	120,5	320	31,38021
21	79,7	256	25,94401
22	175,5	570	25,65789
23	38,1	229	13,86463
24	417,4	879	39,57148
25	343,9	798	35,9127

 

Фондоотдача основных фондов

 

Фондоотдача основных фондов по всей совокупности предприятий рассчитывается по формуле:

 

 

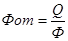
Q- Объем товарной продукции,

Ф- Среднегодовая стоимость основных фонов.

Таблица 1.2

№	Объем товарной продукции, млн. р.	Среднегодовая стоимость основных фондов, млн. р.	Фондоотдача основных фондов
1	163,8	180,1	0,909495
2	236,5	294,5	0,803056
3	843,3	420,8	2,00404
4	1005,9	469,7	2,14158
5	696,3	426,9	1,631061
6	1031,3	552,4	1,866944
7	1361,2	664,6	2,048149
8	1712,9	784,2	2,184264
9	538,9	341,8	1,576653
10	350,4	438	0,8
11	2149,9	825,4	2,604677
12	352,8	179,8	1,96218
13	1187,1	551,5	2,152493
14	262,4	323,4	0,811379
15	438,8	354,2	1,238848
16	1150,5	551,9	2,084617
17	249,4	228,3	1,092422
18	655,3	367,4	1,783615
19	2549,5	930,3	2,740514
20	536,8	179,6	2,988864
21	311,2	404,8	0,768775
22	809,7	473,3	1,710754
23	166,7	180,4	0,924058
24	2185,1	828,3	2,638054
25	2066,2	862,8	2,394761

 

Месячная производительность труда одного рабочего

 

Месячная производительность труда одного рабочего по всей совокупности предприятий рассчитывается по формуле:

 

 

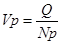
Q- Объем товарной продукции,

Np- Среднесписочная численность рабочих.

Таблица 1.3

№	Объем товарной продукции, млн. р.	Среднесписочная численность рабочих, чел.	Месячная производительность труда одного рабочего, тыс. р/чел.
1	163,8	205	0,0000665854
2	236,5	267	0,0000738140
3	843,3	668	0,0001052021
4	1005,9	714	0,0001174020
5	696,3	544	0,0001066636
6	1031,3	622	0,0001381699
7	1361,2	683	0,0001660810
8	1712,9	728	0,0001960737
9	538,9	526	0,0000853771
10	350,4	267	0,0001093633
11	2149,9	868	0,0002064036
12	352,8	228	0,0001289474
13	1187,1	718	0,0001377786
14	262,4	270	0,0000809877
15	438,8	413	0,0000885391
16	1150,5	695	0,0001379496
17	249,4	364	0,0000570971
18	655,3	595	0,0000917787
19	2549,5	914	0,0002324489
20	536,8	320	0,0001397917
21	311,2	256	0,0001013021
22	809,7	570	0,0001183772
23	166,7	229	0,0000606623
24	2185,1	879	0,0002071578
25	2066,2	798	0,0002157686

 

Средние показатели

 

Средние показатели по всей совокупности предприятий рассчитываются по следующим формулам:

 

; ; ; .

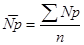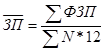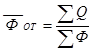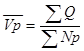Таблица 2.1

№	Среднеспи-сочная численность рабочих, чел.	Среднемесячная заработная плата работника, тыс. р/мес.	Фондоотдача основных фондов	Среднемесячная производительность труда одного рабочего, тыс. р/чел.
1	205	13,65854	0,909495	0,0000665854
2	267	19,72534	0,803056	0,0000738140
3	668	30,06487	2,00404	0,0001052021
4	714	32,13119	2,14158	0,0001174020
5	544	24,46385	1,631061	0,0001066636
6	622	28,00107	1,866944	0,0001381699
7	683	30,7223	2,048149	0,0001660810
8	728	32,77244	2,184264	0,0001960737
9	526	23,65336	1,576653	0,0000853771
10	267	29,15106	0,8	0,0001093633
11	868	39,0649	2,604677	0,0002064036
12	228	29,45906	1,96218	0,0001289474
13	718	32,28877	2,152493	0,0001377786
14	270	21,88272	0,811379	0,0000809877
15	413	18,56336	1,238848	0,0000885391
16	695	31,27098	2,084617	0,0001379496
17	364	16,39194	1,092422	0,0000570971
18	595	26,7507	1,783615	0,0000917787
19	914	41,1105	2,740514	0,0002324489
20	320	31,38021	2,988864	0,0001397917
21	256	25,94401	0,768775	0,0001013021
22	570	25,65789	1,710754	0,0001183772
23	229	13,86463	0,924058	0,0000606623
24	879	39,57148	2,638054	0,0002071578
25	798	35,9127	2,394761	0,0002157686
Среднее	533,64	30,236364	1,947784	0,143742

 

 

Группировка статистических данных

Простая аналитическая группировка

 

Величина равных интервалов определяется по формуле:

 

 

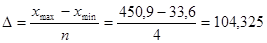
где 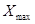и 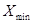 - максимальное и минимальное значение признака;

n - заданное количество интервалов группировки

Анализ данных таблицы 3.1 показывает, что самое большое количество предприятий находится в первой группе, а наименьшее в четвертой. Фондоотдача основных фондов, среднесписочная численность рабочих и среднемесячная заработная плата работника предприятия находятся в прямой зависимости от фонда заработной платы.

 

Комбинационная группировка

 

Согласно исходным данным группировочные признаки: фонд заработной платы и фондоотдача основных фондов, а результативными являются среднесписочная численность рабочих, производительность труда одного рабочего.

∆₁=104,325

 

∆₂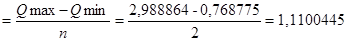

 

Таблица 3.2

Номер групппы	Группы фирм			Номера фирм	Среднесписочная численность рабочих, чел.		Производительность труда одного рабочего, р/чел.
	По Фонду заработной платы, тыс.р.	По фондоотдаче основных фондов			Суммарная	Средняя	Суммарная	Средняя
I	33,6-137,925	0,768775-1,8788195		1,2,10, 14,15, 17,21,23	2271	283,875	0,0006383509	0,0000797939
		1,8788195-2,988864		12,20	548	274	0,0002687390	0,0001343695
Итого:				10	2819	281,9	0,0009070899	0,00009070899
II	137,925-242,25		0,768775-1,8788195	5,6,9,18, 22	2857	571,4	0,0005403664	0,000108073
			1,8788195-2,988864	3	668	668	0,0001052021	0,0001052021
Итого:				6	3525	587,5	0,0006455685	0,000107595
III	242,25- 346,575		0,768775-1,8788195	0	0	0	0	0
			1,8788195-2,988864	4,7,8,13,16,25	4336	722,66666	0,0009710535	0,000161842
Итого:				6	4336	722,66666	0,0009710535	0,000161842
IV	346,575-450,9		0,768775-1,8788195	0	0	0	0	0
			1,8788195-2,988864	11,19,24	2661	887	0,0006460103	0,000215337
Итого:				3	2661	887	0,0006460103	0,000215337

Наибольшее количество предприятий состоит в первой группе, наибольшая производительность труда одного рабочего у предприятий входящих в 4 группу, а так же в этой группе наибольшие показатели среднесписочной численности рабочих. Среднесписочная численность рабочих и производительность труда одного рабочего находятся в прямой зависимости с фондом заработной платы и фондоотдачей основных фондов.

Таблица 4.1

ФЗП(Xi)	Xi-X	(Xi-X)^2
33,6	-160,024	25607,68
63,2	-130,424	17010,42
241	47,376	2244,485
275,3	81,676	6670,969
159,7	-33,924	1150,838
209	15,376	236,4214
251,8	58,176	3384,447
286,3	92,676	8588,841
149,3	-44,324	1964,617
93,4	-100,224	10044,85
406,9	213,276	45486,65
80,6	-113,024	12774,42
278,2	84,576	7153,1
70,9	-122,724	15061,18
92	-101,624	10327,44
260,8	67,176	4512,615
71,6	-122,024	14889,86
191	-2,624	6,885376
450,9	257,276	66190,94
120,5	-73,124	5347,119
79,7	-113,924	12978,68
175,5	-18,124	328,4794
38,1	-155,524	24187,71
417,4	223,776	50075,7
343,9	150,276	22582,88

4840,6

0

368807,2

 

Среднее линейное отклонение – это среднее значение отклонений вариантов признака от их средней величины:

X=193,624

 

,

 

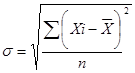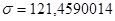
xi – варианты признака

х – средняя величина признака

n – численность единиц совокупности

 

 

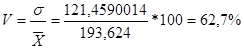
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.

Далее я рассчитываю коэффициенты вариации для простой группировки.

Для первой группы:

Таблица 4.2

Xi	Xi-X10	(Xi-X)^2
33,6	-40,76	1661,378
63,2	-11,16	124,5456
93,4	19,04	362,5216
80,6	6,24	38,9376
70,9	-3,46	11,9716
92	17,64	311,1696
71,6	-2,76	7,6176
120,5	46,14	2128,9
79,7	5,34	28,5156
38,1	-36,26	1314,788

743 ,6

0

5990,344

X=74,36

σ=24,47518

 

 

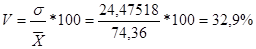
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.

Нужно произвести перегруппировку.

 

Для второй группы:

Таблица 4.3

Xi	Xi-X6	(Xi-X)^2
241	53,4167	2853,34
159,7	-27,8833	777,4803
209	21,4167	458,6736
149,3	-38,2833	1465,614
191	3,41667	11,67361
175,5	-12,0833	146,0069

1125,5

0

5712,788

 

X=187,5833

σ=30,85663

 

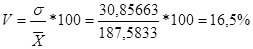
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

Для третьей группы:

Таблица 4.4

Xi	Xi-X6	(Xi-X)^2
275,3	-7,41667	55,00694
251,8	-30,9167	955,8403
286,3	3,583333	12,84028
278,2	-4,51667	20,40028
260,8	-21,9167	480,3403
343,9	61,18333	3743,4

1696,3

0

5267,828

X=282,7167

σ=29,63058

 

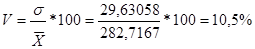
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

 

Для четвертой группы:

Таблица 4.5

Xi	Xi-X	(Xi-X)^2
406,9	-18,1667	330,0278
450,9	25,83333	667,3611
417,4	-7,66667	58,77778
1275,2	0	1056,167

X=425,0667

σ=13,26755

 

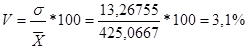
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.

Таблица 5.1

№	Фонд заработной платы, млн. р.	Фондоотдача основных фондов
1	33,6-137,925	0,909494725
		0,803056027
		0,8
		1,9621802
		0,811379097
		1,238848108
		1,092422251
		2,988864143
		0,768774704
		0,92405765
2	137,925-242,25	2,004039924
		1,631061138
		1,866944243
		1,576653013
		1,783614589
		1,710754278
3	242,25- 346,575	2,141579732
		2,048149263
		2,184264218
		2,1524932
		2,084616778
		2,394761242
4	346,575-450,9	2,60467652
		2,740513813
		2,638053845

Я определяю взаимосвязь между фондом заработной платы и фондоотдачей основных фондов.

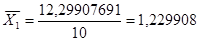
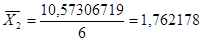
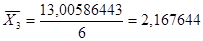
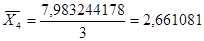
Далее я рассчитываю среднее значение фондоотдачи основных фондов:

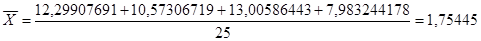
Рассчитываю для каждой группы групповую дисперсию.

Групповая дисперсия рассчитывается по формуле:

 

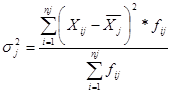
Дисперсия для 1 группы:

Таблица 5.2

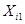
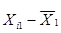
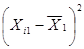
0,909494725	-0,320412965	0,102664468
0,803056027	-0,426851663	0,182202343
0,8	-0,429907691	0,184820622
1,9621802	0,73227251	0,536223028
0,811379097	-0,418528593	0,175166184
1,238848108	0,008940418	0,0000799
1,092422251	-0,137485439	0,018902246
2,988864143	1,758956452	3,0939278
0,768774704	-0,461132987	0,212643632
0,92405765	-0,305850041	0,093544247
Итого:	-

4,600174502

 

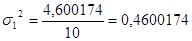
Дисперсия для 2 группы:

Таблица 5.3

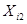
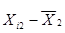
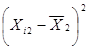
2,004039924	0,24186206	0,05849726
1,631061138	-0,131116726	0,0171916
1,866944243	0,104766379	0,01097599
1,576653013	-0,185524851	0,03441947
1,783614589	0,021436725	0,00045953
1,710754278	-0,051423586	0,00264439
Итого:	-

0,12418823

 

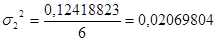
Дисперсия для 3 группы:

Таблица 5.4

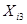
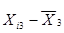
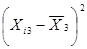
2,141579732	0,005654493	3,19733E-05
2,048149263	-0,087775976	0,007704622
2,184264218	0,048338979	0,002336657
2,1524932	-0,173745039	0,030187338
2,084616778	-0,051308461	0,002632558
2,394761242	0,258836003	0,066996077
Итого:	-

0,073939878

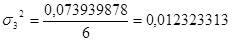
Дисперсия для 4 группы:

Таблица 5.5

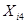
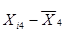
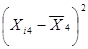
2,60467652	-0,056404872	0,00318151
2,740513813	0,07943242	0,006309509
2,638053845	-0,023027548	0,000530268
Итого:	-

0,010021287

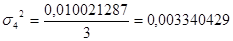
Далее я рассчитываю среднюю внутригрупповую дисперсию :

Внутригрупповая дисперсия находится по формуле:

 

 

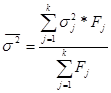
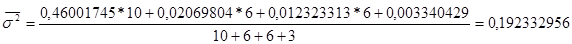
Далее я рассчитываю межгрупповую дисперсию:

Межгрупповая дисперсия рассчитывается по формуле:

 

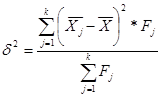
Таблица 5.6

№	Кол-во
1	10	1,229907691	-0,5245424	0,275144748	2,751447479
2	6	1,762177864	0,00772776	0,000059718	0,000358309
3	6	2,167644072	0,41319396	0,170729252	1,024375512
4	3	2,661081393	0,90663128	0,821980286	2,465940859
Итого:	25	-	-	-

6,242122159

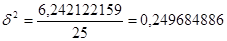
Далее рассчитываю общую дисперсию:

 

 

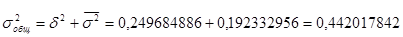
Рассчитываю коэффициент детерминации:

 

 

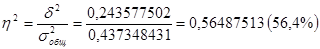
Рассчитываю эмпирическое корреляционное отношение:

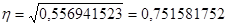
Изменение фонда заработной платы влияет на изменение фондоотдачи основных фондов на 56,4%, между фондом заработной платы и фондоотдачей основных фондов предприятия существует тесная положительная связь.

Таблица 6.1

№	Фонд заработной платы, млн.р.	Фондоотдача основных фондов	Ранг ФЗП	Ранг Ф	dk	d2k
1	33,6	0,909494725	1	5	-4	16
2	63,2	0,803056027	3	3	0	0
3	241	2,004039924	16	15	1	1
4	275,3	2,141579732	19	18	1	1
5	159,7	1,631061138	12	10	2	4
6	209	1,866944243	15	13	2	4
7	251,8	2,048149263	17	16	1	1
8	286,3	2,184264218	21	20	1	1
9	149,3	1,576653013	11	9	2	4
10	93,4	0,8	9	2	7	49
11	406,9	2,60467652	23	22	1	1
12	80,6	1,9621802	7	14	-7	49
13	278,2	2,1524932	20	19	1	1
14	70,9	0,811379097	4	4	0	0
15	92	1,238848108	8	8	0	0
16	260,8	2,084616778	18	17	1	1
17	71,6	1,092422251	5	7	-2	4
18	191	1,783614589	14	12	2	4
19	450,9	2,740513813	25	24	1	1
20	120,5	2,988864143	10	25	-15	225
21	79,7	0,768774704	6	1	5	25
22	175,5	1,710754278	13	11	2	4
23	38,1	0,92405765	2	6	-4	16
24	417,4	2,638053845	24	23	1	1
25	343,9	2,394761242	22	21	1	1
Итого:	4840,6	43,8612527	-	-	-	414

 

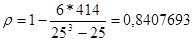
Линейная форма зависимости

 

 

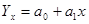
Таблица 7.1

№	x	y	Xy	x2	y2	Yx
1	33,6	0,909494725	30,55902277	1128,96	0,827180655	1,046650876
2	63,2	0,803056027	50,75314092	3994,24	0,644898983	1,177574095
3	241	2,004039924	482,9736217	58081	4,016176017	1,963998029
4	275,3	2,141579732	589,5769001	75790,09	4,586363747	2,115709732
5	159,7	1,631061138	260,4804638	25504,09	2,660360437	1,604401483
6	209	1,866944243	390,1913469	43681	3,485480808	1,822459413
7	251,8	2,048149263	515,7239844	63403,24	4,194915402	2,011767312
8	286,3	2,184264218	625,3548457	81967,69	4,771010175	2,164363632
9	149,3	1,576653013	235,3942949	22290,49	2,485834725	1,558401433
10	93,4	0,8	74,72	8723,56	0,64	1,311151164
11	406,9	2,60467652	1059,842876	165567,61	6,784339776	2,69778729
12	80,6	1,9621802	158,1517241	6496,36	3,850151138	1,254535717
13	278,2	2,1524932	598,8236083	77395,24	4,633226978	2,128536669
14	70,9	0,811379097	57,52677798	5026,81	0,658336039	1,211631825
15	92	1,238848108	113,974026	8464	1,534744636	1,304958849
16	260,8	2,084616778	543,6680558	68016,64	4,345627113	2,051575047
17	71,6	1,092422251	78,2174332	5126,56	1,193386375	1,214727982
18	191	1,783614589	340,6703865	36481	3,181281002	1,742843942
19	450,9	2,740513813	1235,697678	203310,81	7,510415958	2,892402886
20	120,5	2,988864143	360,1581292	14520,25	8,933308863	1,431016679
21	79,7	0,768774704	61,27134387	6352,09	0,591014545	1,250554944
22	175,5	1,710754278	300,2373759	30800,25	2,926680201	1,674286175
23	38,1	0,92405765	35,20659645	1451,61	0,85388254	1,066554744
24	417,4	2,638053845	1101,123675	174222,76	6,95932809	2,744229648
25	343,9	2,394761242	823,5583913	118267,21	5,734881408	2,41913314
Итого:
	4840,6	43,8612527	10123,8557	1306063,56	88,00282561	43,8612527

 

 

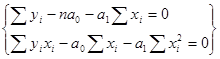
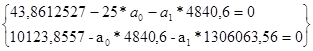
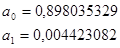
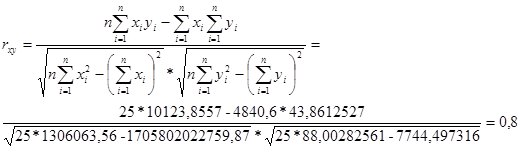
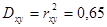
Рисунок 7.1

 

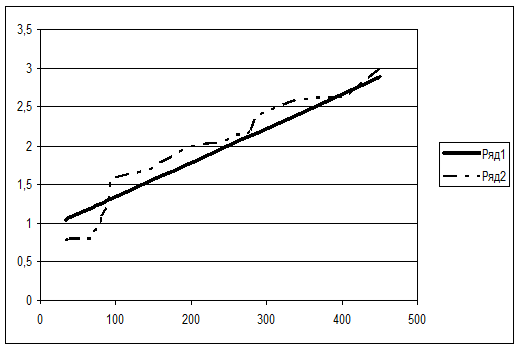
Степенная форма зависимости

 

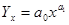
Таблица 7.2

№	x	y	lgx	lgy	lgxlgy	(lgx)2	Yx
1	33,6	0,909494725	1,5263393	-0,041199815	-0,062884896	2,32971159	0,7631503
2	63,2	0,803056027	1,8007171	-0,095254154	-0,171525782	3,242581996	1,0420802
3	241	2,004039924	2,382017	0,301906369	0,719146117	5,674005191	2,0161849
4	275,3	2,141579732	2,4398062	0,330734248	0,806927473	5,952654349	2,1529068
5	159,7	1,631061138	2,2033049	0,21247024	0,468136725	4,854552553	1,6459264
6	209	1,866944243	2,3201463	0,271131348	0,62906439	5,383078789	1,8794161
7	251,8	2,048149263	2,4010557	0,311361603	0,747596561	5,765068598	2,0602409
8	286,3	2,184264218	2,4568213	0,339305171	0,833612189	6,035971136	2,1949018
9	149,3	1,576653013	2,1740598	0,197736125	0,429890162	4,726536048	1,5921726
10	93,4	0,8	1,9703469	-0,096910013	-0,190946341	3,882266813	1,2634054
11	406,9	2,60467652	2,6094877	0,415753795	1,08490441	6,809426003	2,6103113
12	80,6	1,9621802	1,906335	0,292738889	0,558058402	3,634113292	1,1748423
13	278,2	2,1524932	2,4443571	0,332941788	0,813828632	5,974881758	2,1640595
14	70,9	0,811379097	1,8506462	-0,090776185	-0,167994605	3,424891488	1,10286
15	92	1,238848108	1,9637878	0,093018062	0,182667738	3,856462631	1,2540319
16	260,8	2,084616778	2,4163076	0,319026229	0,770865497	5,838542355	2,0962277
17	71,6	1,092422251	1,854913	0,038390538	0,071211108	3,44070232	1,1082156
18	191	1,783614589	2,2810334	0,251301016	0,573226003	5,203113222	1,7977819
19	450,9	2,740513813	2,6540802	0,437831995	1,162041245	7,044141895	2,745871
20	120,5	2,988864143	2,080987	0,475506175	0,989522191	4,330507089	1,4325096
21	79,7	0,768774704	1,9014583	-0,114200916	-0,217148281	3,615543748	1,1683554
22	175,5	1,710754278	2,2442771	0,233187635	0,523337674	5,036779795	1,7243012
23	38,1	0,92405765	1,580925	-0,034300933	-0,054227202	2,499323779	0,8119427
24	417,4	2,638053845	2,6205524	0,421283656	1,103995914	6,867295116	2,6433103
25	343,9	2,394761242	2,5364322	0,379262221	0,9619729	6,433488183	2,4025357
Итого:
	4840,6	43,8612527	54,620195	5,182245088	12,56527822	121,8556397	42,847542

 

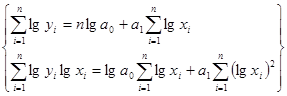
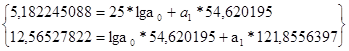
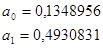
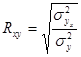
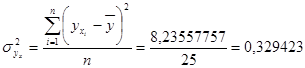
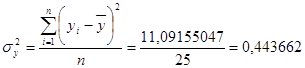
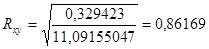
Рисунок 7.2

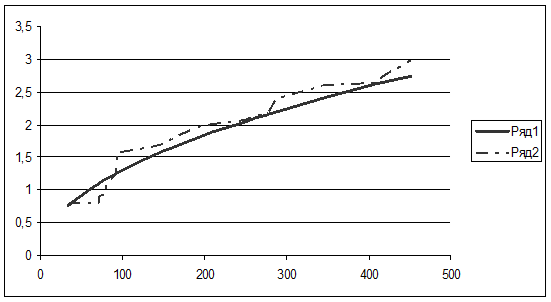
Таблица 7.3

№	X	Y	XY	X2	Y2	Yx
1	85,7625	1,229908	105,479985	7355,206406	1,51267369	1,2471831
2	190,0875	1,762178	334,968011	36133,25766	3,1052713	1,7139097
3	294,4125	2,135925	628,843019	86678,72016	4,56217561	2,1806363
4	398,7375	2,661081	1061,07279	158991,5939	7,08135209	2,6473629
Итого:

969

7,789092

2130,3638

289158,7781

16,2614727

7,789092

 

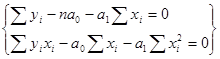
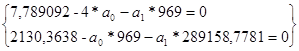
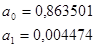
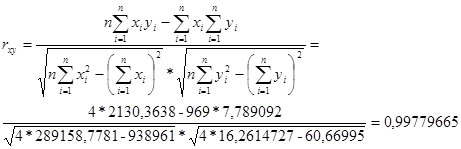
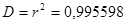
Рисунок 7.3

 

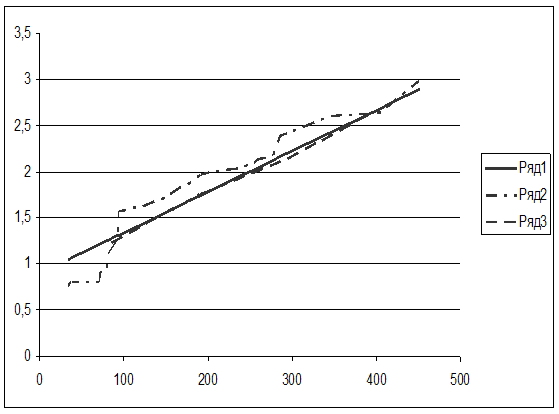
При сравнении пунктов 7.1 и 7.2 видно, что в обоих пунктах коэффициент корреляции достаточно велик, что свидетельствует о сильной и прямой связи между фондом заработной платы и фондоотдачей основных фондов.

Сравнение и анализ расчетов

 

При расчетах в 5, 6 и 7 пунктах видно, что между объемом товарной продукции и среднемесячной заработной платой работника предприятия присутствует прямая положительная связь.

5.

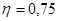
6.

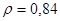
7.

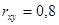
Таблица 9.1

Y	X1	X2	X12	X22	X1X2	X1Y	X2Y	Yx1x2
33,6	0,909495	205	0,82718066	42025	186,446419	30,559023	6888	21,2951101
63,2	0,803056	267	0,64489898	71289	214,415959	50,753141	16874,4	45,9528289
241	2,00404	668	4,01617602	446224	1338,69867	482,97362	160988	261,246605
275,3	2,14158	714	4,58636375	509796	1529,08793	589,5769	196564,2	285,936884
159,7	1,631061	544	2,66036044	295936	887,297259	260,48046	86876,8	194,62464
209	1,866944	622	3,48548081	386884	1161,23932	390,19135	129998	236,569445
251,8	2,048149	683	4,1949154	466489	1398,88595	515,72398	171979,4	269,275905
286,3	2,184264	728	4,77101018	529984	1590,14435	625,35485	208426,4	293,475674
149,3	1,576653	526	2,48583472	276676	829,319485	235,39429	78531,8	184,945851
93,4	0,8	267	0,64	71289	213,6	74,72	24937,8	45,8625521
406,9	2,604677	868	6,78433978	753424	2260,85922	1059,8429	353189,2	368,673556
80,6	1,96218	228	3,85015114	51984	447,377086	158,15172	18376,8	62,7056787
278,2	2,152493	718	4,63322698	515524	1545,49012	598,82361	199747,6	288,05295
70,9	0,811379	270	0,65833604	72900	219,072356	57,526778	19143	47,5439542
92	1,238848	413	1,53474464	170569	511,644269	113,97403	37996	124,295552
260,8	2,084617	695	4,34562711	483025	1448,80866	543,66806	181256	275,734204
71,6	1,092422	364	1,19338638	132496	397,6417	78,217433	26062,4	97,997517
191	1,783615	595	3,181281	354025	1061,25068	340,67039	113645	222,000526
450,9	2,740514	914	7,51041596	835396	2504,82962	1235,6977	412122,6	393,313542
120,5	2,988864	320	8,93330886	102400	956,436526	360,15813	38560	134,289059
79,7	0,768775	256	0,59101454	65536	196,806324	61,271344	20403,2	40,0075298
175,5	1,710754	570	2,9266802	324900	975,129939	300,23738	100035	208,637715
38,1	0,924058	229	0,85388254	52441	211,609202	35,206596	8724,9	32,4873636
417,4	2,638054	879	6,95932809	772641	2318,84933	1101,1237	366894,6	374,59215
343,9	2,394761	798	5,73488141	636804	1911,01947	823,55839	274432,2	331,083208
Итого:

4840,6

43,86125

13341

88,0028256

8420657

26315,9598

10123,856

3252653,3

4840,6

 

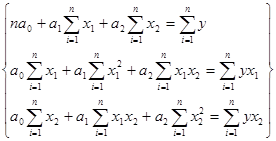
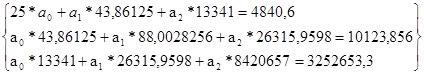
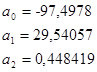
Коэффициент конкордации

 

Коэффициент конкордации находится по формуле:

 

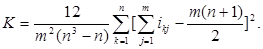
n_i – число неразличимых элементов (рангов) в i –й группе признака X_j ;

m_j – число групп из неразличимых рангов.

Таблица 9.2

 

№	Фонд заработной платы, млн. р.	Фондоотдача основных фондов	Среднесписочная численность рабочих, чел.	Ранги
				ФЗП	Фот	N
1	33,6	0,909495	205	1	5	1
2	63,2	0,803056	267	3	3	5
3	241	2,00404	668	16	15	16
4	275,3	2,14158	714	19	18	19
5	159,7	1,631061	544	12	10	12
6	209	1,866944	622	15	13	15
7	251,8	2,048149	683	17	16	17
8	286,3	2,184264	728	21	20	21
9	149,3	1,576653	526	11	9	11
10	93,4	0,8	267	9	2	6
11	406,9	2,604677	868	23	22	23
12	80,6	1,96218	228	7	14	2
13	278,2	2,152493	718	20	19	20
14	70,9	0,811379	270	4	4	7
15	92	1,238848	413	8	8	10
16	260,8	2,084617	695	18	17	18
17	71,6	1,092422	364	5	7	9
18	191	1,783615	595	14	12	14
19	450,9	2,740514	914	25	24	25
20	120,5	2,988864	320	10	25	8
21	79,7	0,768775	256	6	1	4
22	175,5	1,710754	570	13	11	13
23	38,1	0,924058	229	2	6	3
24	417,4	2,638054	879	24	23	24
25	343,9	2,394761	798	22	21	22

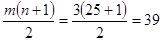
Таблица 9.3

№	Ранги
	Q	ЗП	Фот
1	1	5	1	7	-32	1024
2	3	3	5	11	-28	784
3	16	15	16	47	8	64
4	19	18	19	56	17	289
5	12	10	12	34	-5	25
6	15	13	15	43	4	16
7	17	16	17	50	11	121
8	21	20	21	62	23	529
9	11	9	11	31	-8	64
10	9	2	6	17	-22	484
11	23	22	23	68	29	841
12	7	14	2	23	-16	256
13	20	19	20	59	20	400
14	4	4	7	15	-24	576
15	8	8	10	26	-13	169
16	18	17	18	53	14	196
17	5	7	9	21	-18	324
18	14	12	14	40	1	1
19	25	24	25	74	35	1225
20	10	25	8	43	4	16
21	6	1	4	11	-28	784
22	13	11	13	37	-2	4
23	2	6	3	11	-28	784
24	24	23	24	71	32	1024
25	22	21	22	65	26	676
Итого:	-	-	-	-	-	10676

 

 

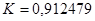
Заключение

 

Настоящая работа ставила перед собой цель освоения практических навыков обработки статистической информации. В процессе работы было рассмотрено 25 предприятий. Вначале были рассчитаны относительные и средние показатели для каждого предприятия. На основе рассчитанных относительных, а так же абсолютных признаков была сделана простая аналитическая группировка по фонду заработной платы, в результате которой был сделан вывод о наличии прямой связи между ним и результативными показателями: фондоотдачей основных фондов, среднесписочной численностью рабочих, среднемесячной заработной платой работника предприятия, производительностью труда одного рабочего.

Затем совокупность предприятий была проверена на однородность по признаку фонд заработной платы, в результате чего было выяснено, что вся совокупность предприятий неоднородна по этому показателю, но одна группа, полученная в результате простой группировки оказалась неоднородна по данному признаку, так как коэффициент вариации в этом случае оказался выше 25%

Затем вся совокупность предприятий была проанализирована по двум признакам: фонд заработной платы и фондоотдачей основных фондов для выявления наличия и тесноты связи.

С использованием дисперсий было вычислено эмпирическое корреляционное отношение 75%. Коэффициент ранговой корреляции равен 84%. Затем были рассчитаны показатели тесноты связи: парный коэффициент корреляции оказался равен 0,8.

Далее был проведен анализ по всей совокупности предприятий на наличие и тесноту множественной связи между результативным признаком фондом заработной платы и двумя факторными признаками: фондоотдачей основных фондов и среднесписочной численностью рабочих.

С использованием рангов был рассчитан коэффициент конкордации – 0,91. Кроме этого был вычислен множественный коэффициент корреляции – 0,97. Поэтому можно утверждать, что между результативным и факторными признаками существует сильная связь. Так же были рассчитаны парные коэффициенты корреляции и частные коэффициенты корреляции, на основе которых можно утверждать, что фонд заработной платы зависит от фондоотдачи основных фондов и среднесписочной численности рабочих.

 

Список литературы

 

1. Богородская Н.А. Статистика. Методы анализа статистической информации:  Методические указания к практическим занятиям / СПбГУАП, СПб., 2008. 158 с.

2. Теория статистики: Учебник / Под ред. Г.Л.Громыко. - 2-е изд., перераб. и доп. - М.: ИНФРА-М, 2005. - 476 с.

Среднемесячная заработная плата работника предприятия

 

Среднемесячная заработная плата рабочего по всей совокупности предприятий рассчитывается по формуле:

 

 

 

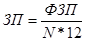
ФЗП- Фонд заработной платы (без учета выплат в различные фонды),

N- Среднесписочная численность работающих, чел.

Таблица 1.1

№	Фонд заработной платы (без учета выплат в различные фонды), млн р	Среднесписочная числен-ность работающих, чел.	Среднемесячная заработная плата работника предприятия, тыс. р/мес.
1	33,6	205	13,65854
2	63,2	267	19,72534
3	241,0	668	30,06487
4	275,3	714	32,13119
5	159,7	544	24,46385
6	209,0	622	28,00107
7	251,8	683	30,7223
8	286,3	728	32,77244
9	149,3	526	23,65336
10	93,4	267	29,15106
11	406,9	868	39,0649
12	80,6	228	29,45906
13	278,2	718	32,28877
14	70,9	270	21,88272
15	92,0	413	18,56336
16	260,8	695	31,27098
17	71,6	364	16,39194
18	191,0	595	26,7507
19	450,9	914	41,1105
20	120,5	320	31,38021
21	79,7	256	25,94401
22	175,5	570	25,65789
23	38,1	229	13,86463
24	417,4	879	39,57148
25	343,9	798	35,9127

 

Фондоотдача основных фондов

 

Фондоотдача основных фондов по всей совокупности предприятий рассчитывается по формуле:

 

 

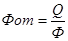
Q- Объем товарной продукции,

Ф- Среднегодовая стоимость основных фонов.

Таблица 1.2

№	Объем товарной продукции, млн. р.	Среднегодовая стоимость основных фондов, млн. р.	Фондоотдача основных фондов
1	163,8	180,1	0,909495
2	236,5	294,5	0,803056
3	843,3	420,8	2,00404
4	1005,9	469,7	2,14158
5	696,3	426,9	1,631061
6	1031,3	552,4	1,866944
7	1361,2	664,6	2,048149
8	1712,9	784,2	2,184264
9	538,9	341,8	1,576653
10	350,4	438	0,8
11	2149,9	825,4	2,604677
12	352,8	179,8	1,96218
13	1187,1	551,5	2,152493
14	262,4	323,4	0,811379
15	438,8	354,2	1,238848
16	1150,5	551,9	2,084617
17	249,4	228,3	1,092422
18	655,3	367,4	1,783615
19	2549,5	930,3	2,740514
20	536,8	179,6	2,988864
21	311,2	404,8	0,768775
22	809,7	473,3	1,710754
23	166,7	180,4	0,924058
24	2185,1	828,3	2,638054
25	2066,2	862,8	2,394761