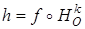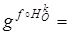
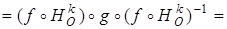
Рассмотрим сдвиг g с осью q и коэффициентом m и подобие , где f – движение, найдем трансформацию g^h. 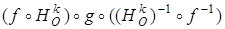. В силу ассоциативности композиции преобразований,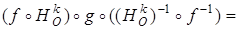 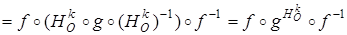. По доказанному в п. 13.3,  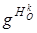есть g ₁ - сдвиг с осью  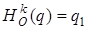и коэффициентом m. Тогда  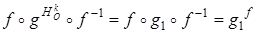По доказанному в пункте 14.3, g ₁ ^f есть косое сжатие с осью f ( q ₁ ) и коэффициентом m. Таким образом, вся искомая трансформация представляет собой косое сжатие с осью  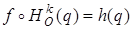и коэффициентом m.

16. Трансформация аффинного преобразования     аффинным преобразованием

16.1. Трансформация косого сжатия произвольным аффинным преобразованием

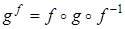Рассмотрим произвольное аффинное преобразование и косое сжатие g с осью q, направлением l и коэффициентом k. Найдем, что представляет собой трансформация косого сжатия g произвольным аффинным преобразованием f – , для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 13).

Точка А при аффинном преобразовании f ^-1 перейдет в точку А₁, которая при косом сжатии g перейдет в точку А₂ такую, что А₁А₂ || l, 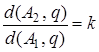. Далее точка А₂ при аффинном преобразовании f перейдет в точку А₃. Заметим, что прямая q ₁ = f ( q ) – инвариантная прямая всей трансформации (по теореме о неподвижных прямых). Из точек А₁ и А₂ проведем перпендикуляры на прямую q – А₁В₁ и А₂В₂, а из точек А и А₃ – на прямую q ₁ – АВ и А₃В₃. Пусть АС и А₃С₃ – образы отрезков А₁В₁ и А₂В₂ при аффинном преобразовании f, значит, А₁В₁||А₂В₂ и  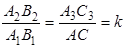(т.к. при косом сжатии сохраняется параллельность прямых и отношение параллельных отрезков), тогда  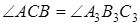(соответственные углы при пересечении параллельных прямых секущей), следовательно, прямоугольные треугольники АВС и А₃В₃С₃ подобны, исходя из этого 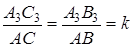. Мы получили, что при этой трансформации расстояние от точки А до прямой q ₁ изменилось в k раз: 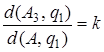. Причем из того, что А₁А₂ || l, следует, что AA ₃ || f ( l ), потому что при косом сжатии сохраняется параллельность прямых, значит, точка А сместилась в направлении f ( l ). Следовательно, в силу произвольности точки А, искомая трансформация есть косое сжатие с осью f ( q ), направлением f ( l ) и коэффициентом k.

17. Решение задач с помощью трансформации преобразований

Задача 1. Даны правильные одинаково ориентированные треугольники OAB, OCD, OEF. Доказать, что середины M, N, P соответственно отрезков BC, DE, AF являются вершинами правильного треугольника. [1]

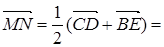
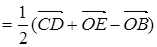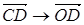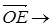
Решение. Из четырехугольника BEDC находим:   (рис. 14). Помня, что результат поворота вектора не зависит от центра поворота, выполним поворот этих векторов на -60°: , , 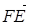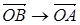. На основании (6) образом вектора  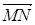будет вектор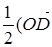 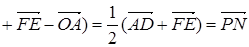. Отсюда и следует, что треугольник MNP правильный.

Задача 2. Найти все перемещения плоскости, перестановочные с осевой симметрией S_l. [«Математика в школе», 1977, №1, задача 1802]

Решение. Из определения (1) следует, что 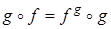. Если f = S_l, то на основании зависимости (3) имеем: 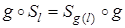. Задача требует найти такие перемещения g, чтобы 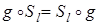. А для этого необходимо и достаточно того, чтобы S_l = S_{g ( l )}, откуда l = g ( l ). Перемещениями, отображающими прямую l на себя, являются: осевая симметрия с осью l, осевые симметрии, оси которых перпендикулярны прямой l, центральные симметрии с центрами на l, переносы параллельно l, переносные симметрии с осью l, тождественные перемещения и только эти преобразования.

 Задача 3. Определить взаимное расположение центров A, B, C и зависимость между коэффициентами k, l, m гомотетий A_k, B_l, C_m, если

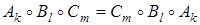                                   ,                                (42)

где точки A, B, C различны и числа k, l, m не равны 1.

Решение. Из данной зависимости (42) получаем: 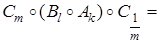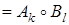, или в принятых обозначениях (1)

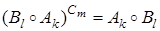                                       .                                    (43)

Рассмотрим отдельно два возможных случая: lk ≠ 1 и lk = 1. В первом случае 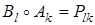, причем 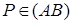. Отсюда получаем: 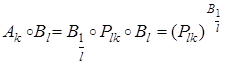. Согласно формуле (24), результатом трансформации гомотетии гомотетией является снова гомотетия. Поэтому 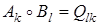, при этом по теореме о неподвижной точке Q = B _{1/ l} ( P ) и, следовательно, 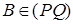. Тогда (43) принимает вид:

,

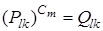где Q = C_m ( P ), и, значит, 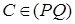. Так как 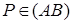, , 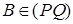, 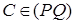то точки A, B, C коллинеарны. Как видим, при lk ≠ 1 для коэффициентов k, l, m дополнительных ограничений не возникает.

При lk = 1 по формуле (22) будет 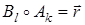, тогда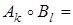 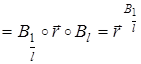 и согласно (26) 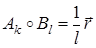. Поэтому (43) принимает вид 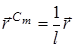, или 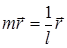 при любом положении точки C. Отсюда lm = 1. Итак, при lk = lm = 1 центры A, B, C гомотетий произвольны.

Задача 4. Точки А, В, С лежат на прямой а, точки А₁, В₁, С₁ – на прямой а₁, параллельной прямой а (рис. 15). Доказать, что точки P = (AB₁) ∩ (A₁B), Q = ( AC ₁ ) ∩ ( A ₁ C ) и R = ( BC ₁ ) ∩ ( B ₁ C ) коллинеарны (теорема Паппа-Паскаля).

Решение. Рассмотрим гомотетии P_k, R_l, Q_m, заданные указанными центрами и парами точек A → B ₁, B ₁ → C, C → A ₁ соответственно. Так как по условию a || a ₁, то Q_m ( A ) = C ₁, R_l ( C ₁ ) = B, P_k ( B ) = A ₁. Замечаем, что 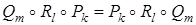, поскольку произведение коэффициентов гомотетий в каждой из этих композиций одно и то же и эти композиции имеют общую пару соответственных точек A → A ₁. На основании предыдущей задачи при lk ≠ 1 точки P, Q, R коллинеарны. Если же lk = lm = 1, то при a || a ₁ это возможно лишь тогда, когда ( PR ) || a и ( PQ ) || a, то есть и в этом случае точки P, Q, R коллинеарны.

Задача 5. Если фигура имеет ось симметрии и единственный центр симметрии, то центр симметрии принадлежит оси симметрии. Доказать.

Решение. Пусть l – ось симметрии и Q – единственный центр симметрии фигуры F, то есть S_l ( F ) = F и Z_Q ( F ) = F. Тогда композиция 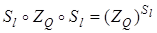 отображает F на себя. Поскольку 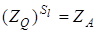, где A = = S_l ( Q ), то Z_A ( F ) = F. Следовательно, точка A является центром симметрии фигуры F. Если бы 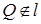, то A ≠ Q, что противоречит условию единственности центра симметрии фигуры F. Значит, .

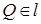Задача 6. Если композиция двух подобий перестановочна и одно из них имеет единственную неподвижную точку, то эта точка неподвижна и при втором подобии. Доказать.

Решение. Из (1) следует, что для любых преобразований f и g всегда выполняется равенство 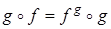. Из него видно, что для того, чтобы 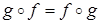, необходимо и достаточно выполнения условия f = f^g. Если теперь f и g – подобия и A – единственная неподвижная точка подобия f (центр подобия), то она будет неподвижной при преобразовании f^g = f. С другой стороны, по теореме о неподвижной точке подобие f^g имеет неподвижную точку g ( A ). В силу единственности неподвижной точки подобия f = f^g должно быть A = g ( A ), то есть A – неподвижная точка подобия g.

Библиографический список

1. Понарин, Я.П. Перемещения и подобия плоскости. [текст]/ Скопец З.А. – К.: Радянська школа, 1981. – 175 с.

2. Понарин, Я.П. Преобразования пространства. [текст] – Киров: Издательство ВГПУ, 2000. – 80 с.

3. Яглом, И.М. Идеи и методы аффинной и проективной геометрии. Часть 1. [текст]/ В.Г. Ашкинузе. – М.: Учпедгиз, 1962. – 247 с.

4. Скопец, З.А. Геометрические миниатюры. [текст]/ Сост. Г.Д. Глейзер. – М.: Просвещение, 1990. – 224 с.

5. Бахман, Ф. Построение геометрии на основе понятия симметрии. [текст] – М.: Наука, 1969.