Подобие φ под подобием ψ 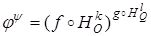 . По формулам (2),
. По формулам (2), 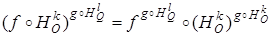 .
. 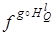 - движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ. По формуле (29),
- движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ. По формуле (29), 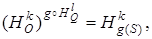
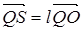 . Тогда
. Тогда
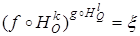 , (30)
, (30)
где ξ - подобие такое, что 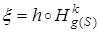 ,
, 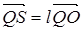 , а h – движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ.
, а h – движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ.
11. Трансформация движения аффинным преобразованием
11.1. Трансформация параллельного переноса аффинным преобразованием
 Рассмотрим произвольную точку М, найдем ее образ при преобразовании
Рассмотрим произвольную точку М, найдем ее образ при преобразовании 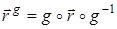 . При преобразовании g -1 она переходит в точку М1 (рис. 3), которая при параллельном переносе
. При преобразовании g -1 она переходит в точку М1 (рис. 3), которая при параллельном переносе 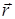 прейдет в точку М2,
прейдет в точку М2, 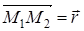 , далее М2 при преобразовании g перейдет в точку М3. Заметим, что вектор
, далее М2 при преобразовании g перейдет в точку М3. Заметим, что вектор 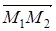 при преобразовании g перейдет в вектор
при преобразовании g перейдет в вектор 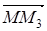 , значит, вся трансформация
, значит, вся трансформация 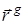 есть параллельный перенос на вектор
есть параллельный перенос на вектор 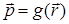 .
.
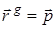 , (31)
, (31)
где 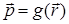 .
.
11.2. Трансформация центральной симметрии аффинным преобразованием
|
 Рассмотрим произвольную точку М, найдем ее образ при преобразовании
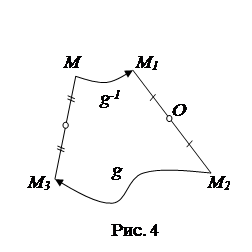
Рассмотрим произвольную точку М, найдем ее образ при преобразовании 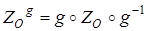 . При преобразовании g -1 она переходит в точку М1 (рис. 4), которая при центральной симметрии ZO прейдет в точку М2, О – середина М1М2, далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ3 (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке g ( O ) будет неподвижной точкой нового преобразования, значит, вся трансформация
. При преобразовании g -1 она переходит в точку М1 (рис. 4), которая при центральной симметрии ZO прейдет в точку М2, О – середина М1М2, далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ3 (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке g ( O ) будет неподвижной точкой нового преобразования, значит, вся трансформация 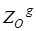 есть центральная симметрия Zg ( O ).
есть центральная симметрия Zg ( O ).
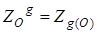 . (32)
. (32)
11.2. Трансформация осевой симметрии аффинным преобразованием
 Рассмотрим произвольную точку М, найдем ее образ при преобразовании
Рассмотрим произвольную точку М, найдем ее образ при преобразовании 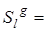
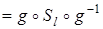 . При преобразовании g -1 она переходит в точку М1 (рис. 5), которая при осевой симметрии Sl прейдет в точку М2,
. При преобразовании g -1 она переходит в точку М1 (рис. 5), которая при осевой симметрии Sl прейдет в точку М2, 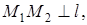
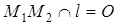 , О – середина М1М2, далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ3 (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), и ее образ – О1 – будет лежать на образе прямой l при преобразовании g - g ( l ). По теореме о неподвижных прямых, прямая g ( l ) будет неподвижной прямой нового преобразования. Заметим также, что если при осевой симметрии прямые, соединяющие точки с их образами, были параллельны, то и после трансформации они будут параллельны и наклонены под одним и тем же углом к прямой g ( l ), значит, вся трансформация
, О – середина М1М2, далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ3 (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), и ее образ – О1 – будет лежать на образе прямой l при преобразовании g - g ( l ). По теореме о неподвижных прямых, прямая g ( l ) будет неподвижной прямой нового преобразования. Заметим также, что если при осевой симметрии прямые, соединяющие точки с их образами, были параллельны, то и после трансформации они будут параллельны и наклонены под одним и тем же углом к прямой g ( l ), значит, вся трансформация 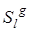 есть косая симметрия Sg ( l ).
есть косая симметрия Sg ( l ).
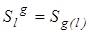 . (33)
. (33)
12. Трансформация гомотетии аффинным преобразованием
 Рассмотрим произвольную точку М, найдем ее образ при преобразовании
Рассмотрим произвольную точку М, найдем ее образ при преобразовании 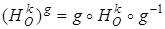 . При преобразовании g -1 она переходит в точку М1 (рис. 6), которая при гомотетии
. При преобразовании g -1 она переходит в точку М1 (рис. 6), которая при гомотетии 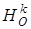 прейдет в точку М2,
прейдет в точку М2, 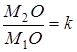 , далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в точку О1 на прямой ММ3, причем
, далее М2 при преобразовании g перейдет в точку М3. Заметим, что точка О при преобразовании g перейдет в точку О1 на прямой ММ3, причем 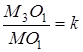
 (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке точка О1 будет неподвижной при новом преобразовании, значит, вся трансформация
(т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке точка О1 будет неподвижной при новом преобразовании, значит, вся трансформация 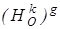 есть гомотетия
есть гомотетия 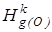 .
.
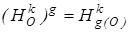 . (35)
. (35)
13. Трансформация аффинного преобразования гомотетией
Далее будем предполагать, что аффинные преобразования g и g -1 заданы аналитически.
g: 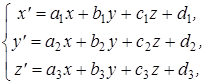 g -1:
g -1: 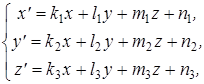 где образы начала координат и базисных векторов при преобразовании g имеют координаты: O ’( d 1 , d2, d 3 ),
где образы начала координат и базисных векторов при преобразовании g имеют координаты: O ’( d 1 , d2, d 3 ), 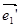 ( a 1 , a 2 , a 3 ),
( a 1 , a 2 , a 3 ), 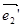 ( b 1 , b 2 , b 3 ),
( b 1 , b 2 , b 3 ), 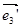 ( c 1 , c 2 , c 3 ), а при преобразовании g -1 O ’’( n 1 , n 2 , n 3 ),
( c 1 , c 2 , c 3 ), а при преобразовании g -1 O ’’( n 1 , n 2 , n 3 ), 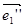 ( k 1 , k 2 , k 3 ),
( k 1 , k 2 , k 3 ), 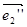 ( l 1 , l 2 , l 3 ),
( l 1 , l 2 , l 3 ), 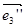 ( m 1 , m 2 , m 3 ).
( m 1 , m 2 , m 3 ).
Известно, что движение является частным случаем аффинного преобразования, значит, движение под аффинным преобразованием, как композиция аффинных преобразований, также будет аффинным преобразованием.
13.1. Трансформация произвольного аффинного преобразования гомотетией
Выберем систему координат таким образом, чтобы центр гомотетии совпадал с началом координат, тогда 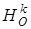 будет задаваться аналитически следующим образом.
будет задаваться аналитически следующим образом.
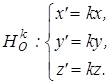 Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании
Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании 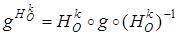 . При гомотетии
. При гомотетии 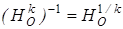 точка М переходит в точку М1( x / k , y / k , z / k ). Далее, при аффинном преобразовании g М1 переходит в точку М2(
точка М переходит в точку М1( x / k , y / k , z / k ). Далее, при аффинном преобразовании g М1 переходит в точку М2( 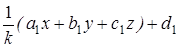 ,
, 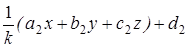 ,
, 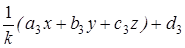 ). M 2 при гомотетии
). M 2 при гомотетии 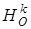 переходит в М3(
переходит в М3( 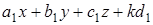 ,
, 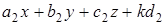 ,
, 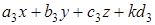 ). Тогда
). Тогда 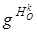 - аффинное преобразование, аналитически оно задается следующим образом.
- аффинное преобразование, аналитически оно задается следующим образом.
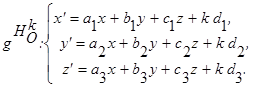 (34)
(34)
Мы получили, что
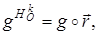 (35)
(35)
где 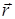 - параллельный перенос,
- параллельный перенос, 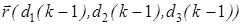 .
.
Дата: 2019-07-30, просмотров: 303.