Рассмотрим гомотетию 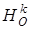 и сдвиг g с осью q и коэффициентом m. Найдем, что представляет собой трансформация сдвига гомотетией – 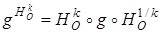, для этого возьмем произвольную точку А и найдем ее образ при данной трансформации (рис. 8).

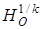Точка А при гомотетии  перейдет в точку А₁, которая при сдвиге перейдет в точку А₂ такую, что А₁А₂ || q, 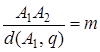. Точка А₂ при гомотетии  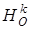перейдет в точку А₃. Заметим, что прямая  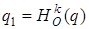– инвариантная прямая всей трансформации (по теореме о неподвижных прямых). Из точки А₁ проведем перпендикуляр на прямую q А₁В₁, а из точки А – на прямую q ₁ – АВ. Тогда АВ – образ отрезка А₁В₁ при гомотетии 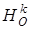, также АА₃ – образ отрезка А₁А₂ при гомотетии 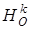, значит,  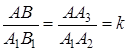и АА₃||А₁А₂||q||q₁, (потому что при гомотетии прямая переходит в параллельную ей прямую), следовательно,  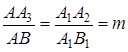и АА₃||q₁. Мы получили, что при этой трансформации точка А смещается параллельно прямой q₁ на расстояние, пропорциональное ее расстоянию от прямой q₁: 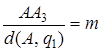. Следовательно, в силу произвольности точки А, искомая трансформация есть сдвиг с осью  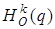и коэффициентом m.

14. Трансформация аффинного преобразования движением

14.1. Трансформация произвольного аффинного   преобразования движением

14.1.1. Трансформация аффинного преобразования параллельным переносом

Данную трансформацию рассмотрим в пространстве. Пусть параллельный перенос задан вектором 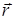, 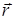( a , b , c ). Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании 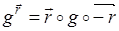. При параллельном переносе  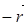точка М переходит в точку М₁( x - a , y - b , z - c ). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂( a ₁ x + b ₁ y + + c ₁ z - aa ₁ - bb ₁ - cc ₁ + d ₁ , a ₂ x + b ₂ y + c ₂ z - aa ₂ - bb ₂ - cc ₂ + + d ₂ , a ₃ x + b ₃ y + c ₃ z - aa ₃ - bb ₃ - cc ₃ + d ₃ ). M ₂ при параллельном переносе  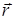переходит в М₃ ( a ₁ x + b ₁ y + c ₁ z - aa ₁ - bb ₁ - cc ₁ + d ₁ + a , a ₂ x + b ₂ y + c ₂ z - aa ₂ - bb ₂ - cc ₂ + d ₂ + + b , a ₃ x + b ₃ y + c ₃ z - aa ₃ - bb ₃ - cc ₃ + d ₃ + c ) (п. 13). Тогда - аффинное преобразование, аналитически оно задается следующим образом.

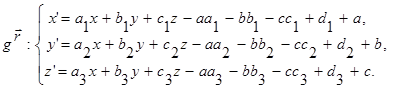                               (36)

Мы получили, что

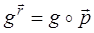                                                ,                                           (37)

где 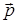(- aa₁ - bb₁ - cc₁ + d₁ + a, - aa₂ - bb₂ - cc₂ + d₂ + b, - aa₃ - bb₃ - cc₃ + d₃ + c).

14.1.2. Трансформация аффинного преобразования        центральной симметрией

Рассмотрим центральную симметрию Z_O в пространстве, выберем систему координат таким образом, чтобы центр симметрии О совпал с началом координат, тогда О(0, 0, 0). Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании 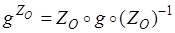. Т.к. центральная симметрия инволютивна, то 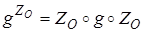. При центральной симметрии Z_O точка М переходит в точку М₁(- x , - y , - z ). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(- a ₁ x - b ₁ y - c ₁ z + d ₁ , - a ₂ x - b ₂ y - c ₂ z + d ₂ , - a ₃ x - b ₃ y - c ₃ z + d ₃ ) (п. 13). M ₂ при центральной симметрии Z_O переходит в М₃( a ₁ x + b ₁ y + c ₁ z - d ₁ , a ₂ x + b ₂ y + c ₂ z - d ₂ , a ₃ x + b ₃ y + c ₃ z - d ₃ ). Тогда 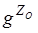- аффинное преобразование, аналитически оно задается следующим образом.

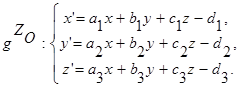                                                               (38)

Мы получили, что

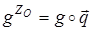                                                ,                                           (39)

где 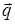(-2 d ₁ , -2 d ₂ , -2 d ₃ ).

14.1.3. Трансформация аффинного преобразования                осевой симметрией

Рассмотрим осевую симметрию S_l в пространстве, выберем систему координат таким образом, чтобы ось симметрии l совпала с осью OZ, тогда S_l будет задаваться следующим образом. 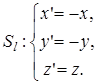 Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании 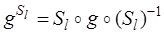. Т.к. осевая симметрия инволютивна, то 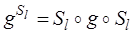. При осевой симметрии S_l точка М переходит в точку М₁(- x , - y , z ). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂(- a ₁ x - b ₁ y + c ₁ z + d ₁ , - a ₂ x - b ₂ y + c ₂ z + d ₂ , - a ₃ x - b ₃ y + c ₃ z + d ₃ ) (п. 13). M ₂ при осевой симметрии S_l переходит в М₃( a ₁ x + b ₁ y - c ₁ z - d ₁ , a ₂ x + b ₂ y - c ₂ z - d ₂ , a ₃ x + b ₃ y - c ₃ z - d ₃ ). Тогда 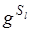- аффинное преобразование, аналитически оно задается следующим образом.

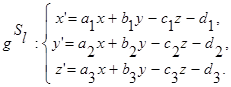                                                                (40)

14.1.4. Трансформация аффинного преобразования                 зеркальной симметрией

Рассмотрим зеркальную симметрию S _α – преобразование постраноства, выберем систему координат таким образом, чтобы плоскость симметрии α совпала с плоскостью XOY, тогда S_α будет задаваться следующим образом. 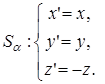 Рассмотрим произвольную точку М( x , y , z ), найдем ее образ при преобразовании 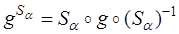. Т.к. зеркальная симметрия инволютивна, то 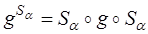. При зеркальной симметрии S _α точка М переходит в точку М₁( x , y , - z ). Далее, при аффинном преобразовании g точка М₁ переходит в точку М₂( a ₁ x + b ₁ y - c ₁ z + d ₁ , a ₂ x + b ₂ y - c ₂ z + d ₂ , a ₃ x + b ₃ y - c ₃ z + d ₃ ) (п. 13). M ₂ при зеркальной симметрии S _α переходит в М₃( a ₁ x + b ₁ y - c ₁ z + d ₁ , a ₂ x + b ₂ y - c ₂ z + d ₂ , - a ₃ x - b ₃ y + c ₃ z - d ₃ ). Тогда 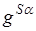- аффинное преобразование, аналитически оно задается следующим образом.

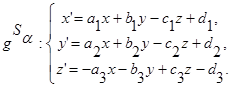                                                                (41)