Векторные диаграммы напряжения и токов                        двухфазном КЗ на землю.

Граничные условия:

1. I_A^(1,1)=0;

2. U_В^(1,1)=0;

3. U_С^(1,1)=0;

U_A1 = 1/3 (U_A + аU_В + аU_С)

U_А2 = 1/3 (U_A + а²U_В + аU_С)

U_А0 = 1/3 (U_A + U_В + U_С)

Отсюда U_A1 = U_A2 = U_A0 = 1/3 U_A или U_A^(1,1) = 3U_A1 = 3U_A2 = 3U_A0

I_A^(1,1) = 0

I_A1 + I_A2 + I_A0 = 0 или

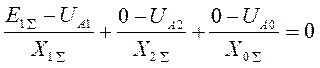, упростим, зная U_A1 = U_A2 = U_A0

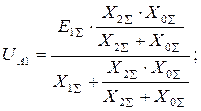 используя выражение U_А1 = Е_1S - X_1S× I_1.

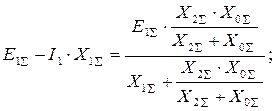 отсюда получим

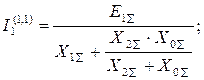 распишем это выражение

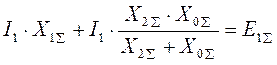, или .

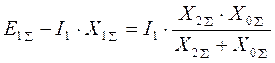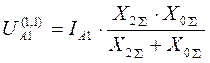, U_A1^(1,1) = I_A1×X_D^(1,1)

U_A2 = U_A0

j×I_A2×X_2S = j×I_A0×X_0S . прибавим к обеим частям равенства по j×I₂×X_0S.

j×I₂×X_0S + j×I_A2×X_2S = j×I_A0×X_0S + j×I₂×X_0S.

j×I_A2×(X_0S +X_2S) = j×(I_A0 + I_A2)×X_0S. Так как I_A2 + I_A0 = - I_A1

,

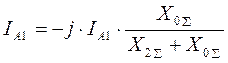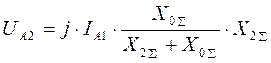
U_A2 = U_A0 . прибавим к обеим частям равенства j×I_А0×X_2S. Получим:

,

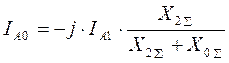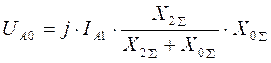
полные токи повреждённых фаз:

I_KB = а²I_A1 + аI_A2 + I_A0

I_KC = аI_A1 + а²I_A2 + I_A0

Подставив в эти выражения найденные ранее I_A2 , I_A0

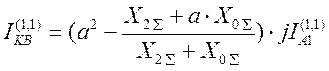
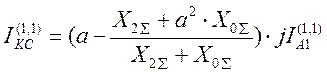. Используя выражение I_K⁽ⁿ⁾=m⁽ⁿ⁾×I_A1⁽ⁿ⁾ получим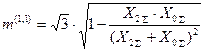

Лекция 15: «Комплексные схемы замещения для несимметричного КЗ».

Для расчёта несимметричного КЗ на статических моделях используют комплексные схемы замещения. Их нетрудно получить на основе соотношений, установленных в предыдущих лекциях.

Если условно обозначить схемы различных последовательностей через прямоугольники, то в соответствии с правилом эквивалентности прямой последовательности получим схемы:

В этих схемах буквами Н и К обозначены начала и концы схем соответствующих последовательностей. Нужно отметить, что при моделирование однофазного КЗ напряжение U_K1 и U_K0 нужно замерять не относительно общей заземлённой точки комплексной схемы замещения, а относительно потенциалов точек Н₂ и Н₀.

Правило эквивалентности прямой последовательности.

Соотношения, полученные для токов прямой последовательности при разных видах КЗ, можно переписать в общем виде:

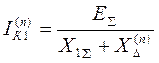(1)

здесь X_D⁽ⁿ⁾ – дополнительное сопротивление, зависящее от вида КЗ:

X _D⁽³⁾ = 0; X _D⁽²⁾ = Х_{2 S};     X _D⁽¹⁾ = Х_{2 S} + Х_{0 S};    X _D^(1,1) = Х_{2 S} ¤ ¤ Х_{0 S}.

Так как токи в фазах пропорциональны току прямой последовательности, то в общем виде модуль фазного тока в месте повреждения для любого вида КЗ можно определить по формуле:

I_K⁽ⁿ⁾=m⁽ⁿ⁾×I_A1⁽ⁿ⁾,   (2)

 где m⁽ⁿ⁾ – коэффициент вида КЗ.

Анализируя формулу (1) можно сформулировать так называемое правило эквивалентности прямой последовательности:

Ток прямой последовательности любого вида несимметричного КЗ можно определить как ток при трёхфазном КЗ в точке, удалённой от действительной точки КЗ на величину дополнительного сопротивления X _D^{( n)}, которое не зависит от параметров схемы прямой последовательности и для каждого вида короткого замыкания определяется результирующими сопротивлениями обратной и нулевой последовательностей относительно рассматриваемой точки схемы.