Несимметрия бывает трёх видов: поперечная, продольная и сложная. К поперечной несимметрии относятся случаи, возникающие при однофазном КЗ на землю, при двухфазном КЗ и двухфазном КЗ на землю. К продольной несимметрии относятся случаи, возникающие при различных фазных сопротивлениях или при обрыве одной или двух фаз. Сложная несимметрия является комбинацией поперечной и продольной несимметрии. Например, однофазное КЗ на землю с обрывом фазы.
Любой несимметричный ток или напряжение КЗ можно выразить с помощью симметричных составляющих. Это значительно упрощает анализ переходных процессов, так как симметричные составляющие определённой последовательности (прямой, обратной, нулевой) связаны линейным законом с симметричными составляющими напряжений тех же последовательностей. Любой вид несимметрии в трёхфазной сети можно выразить с помощью трёх симметричных составляющих.
 |
До сих пор нами были рассмотрены переходные процессы в симметричных трёхфазных системах. В силу симметричности этих систем их схемы замещения составлялись лишь для одной, так называемой расчётной фазы. При этом процессы в остальных фазах считались аналогичными процессам в расчётной.
При нарушении симметрии вместо одной несимметричной трёхфазной схемой рассчитываются три симметричные, значительно более простые схемы. Такой подход возможен на основе использования известного из курса ТОЭ метода симметричных составляющих: DU1=jX1 ×I1, здесь сопротивления Х1, Х2, Х0 - сопротивления DU2=jX2 ×I2, прямой, обратной и нулевой последовательнос- DU0=jX0 ×I0. тей. В общем случае, для одного и того же эле-
мента их величины неодинаковы.
Уравнения связи между симметричными составляющими и фазными величинами:
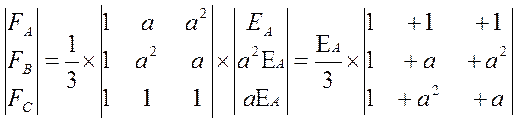
здесь оператор а=еj120 °= -0.5+j0.87, а оператор а2=е-j120 °= -0.5-j0.87.
С помощью операторов а и а2 осуществляется сдвиг фаз В и С относительно фазы А.
При разложении симметричной трёхфазной системы векторов ЕА, ЕВ=а2× ЕА, ЕС= а×ЕА на симметричные составляющие величины составляющих обратной и нулевой последовательностей получаются равными нулю:
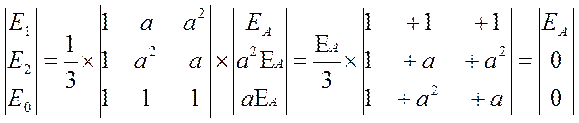
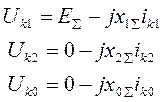следовательно, ЭДС генераторов и других источников питания, создающих симметричную трёхфазную систему ЭДС, должны учитываться лишь в схеме прямой последовательности, а в схемах обратной и нулевой последовательностей ЭДС равны нулю. Поэтому для определения симметричных составляющих напряжения точки КЗ используют выражения:
 |
где UК1, UК2, UК0 -симметричные составляющие напряжения в точке КЗ;
IК1 , IК2 , IК0 - симметричные составляющие тока, притекающего к точке
КЗ;
Х1S , Х2S , Х0S - результирующие сопротивле-
ния схем прямой, обратной и
нулевой последовательностей относительно точки КЗ.
Вышеуказанные три уравнения содержат шесть неизвестных: UК1 , UК2 , UК0, IК1 , IК2 , IК0. Для решения этих уравнений необходимы ещё три уравнения, которые составляют исходя из граничных условий, характеризующих каждый вид несимметричного КЗ.
Дата: 2019-07-30, просмотров: 271.
