Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Схема ПП является обычной схемой, которую составляют при симметричном КЗ. Если для расчета используется метод спрямленных характеристик, то тогда схему ПП можно воспроизвести для произвольного момента времени. В этом случае генераторы входят в схему замещения своими Е_t и Х_t для заданного момента времени. При использовании метода расчетных кривых генераторы входят в схему замещения своими Х_d’’. Токи ОП циркулируют по тем же путям, что и токи ПП, поэтому схемы замещения ПП и ОП совпадают. Отличие состоит в том, что в схеме ОП ЭДС всех генераторов Е₂=0.

Началом схемы ПП и ОП считают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей.

Концом схемы ПП и ОП считают точку, где возникла рассматриваемая несимметрия.

Схема нулевой последовательности.

Ток НП по существу является однофазным током, разветвленным между тремя фазами и возвращающимся через землю, поэтому циркуляция токов НП значительно отличается от путей циркуляции токов ПП и ОП. Схема НП в значительной мере определяется соединением обмоток трансформаторов и автотрансформаторов.

Составление схемы НП следует начинать от точки, где возникла несимметрия, считая, что в этой точке три фазы замкнуты между собой накоротко и к ней приложено напряжение НП (U₀).

Трансформация токов НП возможна при соблюдении определенных условий. Так, в трансформаторе с соединением обмоток U₀/D, наведенный в треугольнике ток НП не выходит за его пределы. Следовательно, вся сеть за треугольником в схему замещения НП не входит. Пример:

 

 

В трансформаторе с соединением обмоток U₀/U₀ трансформация токов НП возможна при условии, что в каждой обмотке обеспечен путь для этих токов. При соблюдении этого условия в схему НП входят как трансформатор, так и все элементы, по которым протекают токи НП с обоих сторон трансформатора.

Сопротивление, через которое заземлена нейтраль трансформатора, генератора, двигателя и нагрузки должно быть введено в схему НП утроенной величиной. Это объясняется тем, что схему замещения НП составляют для одной фазы, а на самом деле через это сопротивление будет протекать сумма токов НП трех фаз: U=Х_N×3I₀=I₀×3X_N. 

 

Лекция 14: «Токи и напряжения в месте несимметричного КЗ».

Для расчётов токов и напряжений в месте КЗ предварительно определяют Е_S и Х_S1 в схеме ПП, Х_S2 и Х_S0 – в схеме ОП и НП. Для упрощения анализа принимают, что КЗ происходит на холостом ответвлении, сопротивления фаз которого относительно точки КЗ равны нулю. Тогда токи в фазах этого ответвления можно считать токами в месте КЗ.

В качестве рабочей фазы, для которой записывают расчётные выражения, принимают фазу А.

Двухфазное КЗ.

 

                                       

Векторные диаграммы напряжений и токов

                                           двухфазного КЗ.

Граничные условия в месте КЗ:

1 I_KA⁽²⁾=0 ;

2 I_KВ⁽²⁾= - I_KС⁽²⁾;

3 U_KВ⁽²⁾= U_KС⁽²⁾;

Перепишем (2): I_KВ⁽²⁾ + I_KС⁽²⁾ = 0 (4).

Сложив (1) и (4), получим: I_KA⁽²⁾ + I_KВ⁽²⁾ + I_KС⁽²⁾ = 0, то есть система токов уравновешенная и I_K0=1/3 ×(I_KA +I_KB +I_KC) = 0.

Перепишем (1) через симметричные составляющие:

I_KA⁽²⁾ = I_KA1⁽²⁾ + I_KA2⁽²⁾ + I_KA0⁽²⁾ = 0.

Так как I_KA0⁽²⁾ = 0, то I_KA1⁽²⁾ = - I_KA2⁽²⁾ (5).

Выразим U_KВ⁽²⁾ и U_KС⁽²⁾ через симметричные составляющие:

U_KВ⁽²⁾ = а²× U_KА1 +а× U_KА2 + U_KА0.

U_KС⁽²⁾ = а× U_KА1 +а²× U_KА2 + U_KА0.

Из выражения (3) следует:

(а² – а)× U_KА1 +(а-а²)× U_KА2 = 0    

(а² – а)×( U_KА1 - U_KА2) = 0

так как (а² – а) ¹0, то U_KА1 = U_KА2 (6).

Вспомним, что U_KА1⁽²⁾=Е_S - jХ_1S×I_KA1 и U_KА2 = 0 – jХ_2S×I_KA2.

 

С учётом (5) и (6), имеем

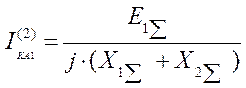(7)

токи в фазах:

I_KA⁽²⁾ = I_KA1⁽²⁾ + I_KA2⁽²⁾ + I_KA0⁽²⁾ = 0

I_KB⁽²⁾ = а²I_KA1⁽²⁾ + аI_KA2⁽²⁾ + I_KA0⁽²⁾ = (а² – а)× I_KА1 = - jÖ3× I_KA1⁽²⁾

I_KC⁽²⁾ = аI_KA1⁽²⁾ + а²I_KA2⁽²⁾ + I_KA0⁽²⁾ = (а – а²)× I_KА1 = + jÖ3× I_KA1⁽²⁾

 

Напряжения в точке КЗ:

Так как U_K0⁽²⁾ = jX_0S× I_KA0⁽²⁾ = 0, то

U_KА⁽²⁾ = U_KА1 + U_KА2 = 2 U_KА1 = - j2×X_2S× I_KA2⁽²⁾ = + j2×X_2S× I_KA1⁽²⁾

U_KВ⁽²⁾ = а²× U_KА1 +а× U_KА2 = - U_KА1 = j2×X_2S× I_KA2⁽²⁾ = - j2×X_2S× I_KA1⁽²⁾ 

U_KС⁽²⁾ = а× U_KА1 +а²× U_KА2 = - U_KА1 = U_KВ⁽²⁾

Однофазное КЗ.

 

 

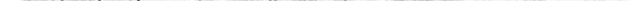
                          Векторные диаграммы напряжения и токов                                           однофазного КЗ на землю.

 

Граничные условия для однофазного КЗ:

1. U_KA⁽¹⁾  = 0 ;

2. I_KВ⁽¹⁾ = 0 ;

3. I_KC⁽¹⁾ = 0 ;

Симметричные составляющие токов с учётом (2) и (3):

I_KA1⁽¹⁾ = 1/3 (I_KA⁽¹⁾ + аI_KВ⁽¹⁾ + а²I_KС⁽¹⁾ ) = 1/3 I_KA⁽¹⁾

I_KА2⁽¹⁾ = 1/3 (I_KA⁽¹⁾ + а²I_KВ⁽¹⁾ + аI_KС⁽¹⁾ ) = 1/3 I_KA⁽¹⁾

I_KА0⁽¹⁾ = I_KA⁽¹⁾ + I_KВ⁽¹⁾ + I_KС⁽¹⁾ = 1/3 I_KA⁽¹⁾

Отсюда видно, что I_KA1⁽¹⁾ = I_KА2⁽¹⁾ = I_KА0⁽¹⁾ = 1/3 I_KA⁽¹⁾

Для повреждённой фазы:

U_KА⁽¹⁾ = U_KА1 + U_KА2 + U_KА0 = 0 (4)

Вспомним три уравнения с шестью неизвестными, составленными для схем замещения ПП, ОП и НП:

Е_1S = U_KA1 + jХ_1S×I_KA1

0 = U_KA2 + jХ_2S×I_KA2 (5)

0 = U_KA0 + jХ_0S×I_KA0

 

Просуммируем систему уравнений (5):

Е_S - jХ_1S×I_KA1 - jХ_2S×I_KA2 - jХ_S0×I_KA0  = U_KА1 + U_KА2 + U_KА0 = 0

Откуда:

;

 

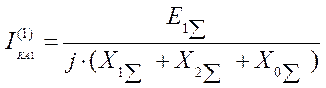Ток в повреждённой фазе I_KA⁽¹⁾ = 3 I_KA1⁽¹⁾.

Симметричные составляющие напряжения в месте КЗ:

U_KА2⁽¹⁾ = 0 - j×X_2S× I_KA2⁽¹⁾ = - j×X_2S× I_KA1⁽¹⁾

U_KА0⁽¹⁾ = 0 - j×X_0S× I_KA0⁽¹⁾ = - j×X_0S× I_KA1⁽¹⁾

 

Из уравнения (4) U_KА⁽¹⁾ = - (U_KА2 + U_KА0 )= j×(X_2S + X_0S )×I_KA1⁽¹⁾

Фазные напряжения в точке КЗ:

U_KВ⁽¹⁾ = а²× U_KА1 +а× U_KА2 + U_KА0

U_KС⁽¹⁾ = а× U_KА1 +а²× U_KА2 +U_KА0

Векторные диаграммы токов и напряжений показаны в начале темы.