Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.

Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.

Рис.1.7 Варианты перекрытия видимости антенн препятствием

Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением

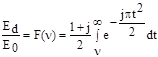, (1.31)

где Е_{0 -} напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F (n) - комплексный интеграл Френеля. Значение интеграла F (n) определяется из графиков и таблиц.

Коэффициент дифракционного усиления с препятствием (обычно он меньше 1) по сравнению со свободным пространством

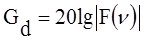, дБ. (1.32)

График этой функции показан на рис.1.8

G_d, дБn

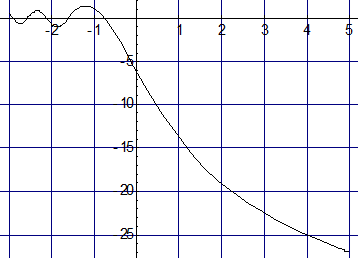
Рис.1.8 Зависимость коэффициента дифракционного усиления от значения параметра дифракции n

Приближенно можно считать:

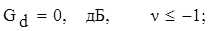 (1.33a)

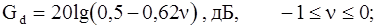 (1.33б)

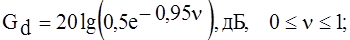 (1.33в)

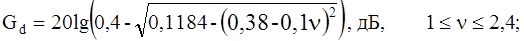 (1.33г)

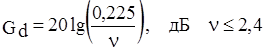 (1.33д)

Дифракция на нескольких клиньях

Если на пути между излучателем и приемником имеется несколько препятствий, то все они аппроксимируются одним эквивалентным препятствием (рис.1.9).

Рис.1.9 Эквивалентное клиновидное препятствие в задаче связи с двумя препятствиями

Эта модель хорошо работает для двух препятствий, для нескольких - возникают определенные математические трудности.

Рассеяние радиоволн

Потери от рассеяния радиоволн на препятствиях обычно много меньше потерь отражения и дифракции. Это объясняется тем, что рассеяние волн происходит во всех направлениях (на таких объектах, как мачты, лампы, деревья и т.д.).

Плоские поверхности с размерами много больше длины волны могут моделироваться как отражающие поверхности. Однако наличие неровностей изменяет отражение. Неровность поверхности определяется критерием Релея, который определяет критическую высоту h_c неровностей при падении волны под углом q_i:

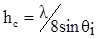. (1.34)

Поверхность считается гладкой, если разброс минимальных и максимальных высот меньше h_c. Для неровных поверхностей коэффициент отражения r умножается на коэффициент потерь рассеяния p_s.

Полагая, что высота неровностей h распределена случайным образом с гауссовым законом распределения, коэффициент потерь рассеяния

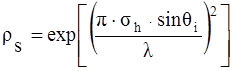, (1.35)

где s_h - стандартная девиация высоты поверхности вокруг среднего значения высоты. После некоторых уточнений коэффициент потерь рассеяния с хорошим совпадением с практикой определяется выражением

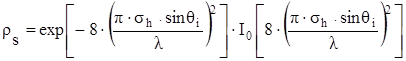, (1.36)

где I_{0 -} функция Бесселя первого рода нулевого порядка. Коэффициент отражения электромагнитного поля для неровностей h>h_c определяется выражением

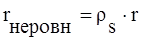. (1.37)

Степень рассеяния радиоволн от препятствий больших размеров, например, крупных домов, может характеризоваться поперечником рассеяния. Поперечник рассеяния объекта (RCS) определяется как отношение плотности потока мощности рассеянного поля в направлении приемника к плотности потока мощности, падающей на рассеивающий объект, и имеет размерность м². Анализ основан на геометрической теории дифракции и физической оптике и может быть использован для задач расчета поля, рассеянного большими зданиями. Для городских условий используется бистатическое уравнение излучения, описывающее распространение волны в свободном пространстве и поле, рассеянное между объектами и затем переизлученное в направлении приемника.

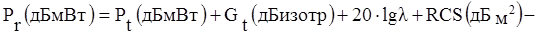
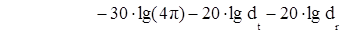, (1.38)

где d_t и d_{r -} расстояние от рассеивающего объекта до излучателя и приемника. Это уравнение корректно для дальней зоны излучателя и приемника.