Пусть плоская волна падает нормально на границу I плоского слоя диэлектрика (рисунок 1.3, а). Часть энергии волны отразится от границы I и будет распространяться в обратном направлении, а часть проникнет сквозь границу I и будет распространяться в прямом направлении до границы II. Здесь будет наблюдаться аналогичная картина: часть энергии проникнет сквозь границу II, а другая часть отразится от этой границы и будет распространяться к границе I и т.д.
Рис.1.3 Волны вблизи диэлектрического слоя:
а - нормальное падение волны, б - косое падение волны.
Введем следующие обозначения: A - волна, падающая на слой диэлектрика; B - волна, движущаяся от границы I влево (сумма первичной отраженной волны и всех волн, проникающих через границу I справа); C - волна, движущаяся в слое слева направо (сумма первичной проникающей через границу I волны и всех волн, отраженных от этой границы внутрь слоя); D - волна, движущаяся в слое справа налево (сумма всех волн, отраженных от границы II); F - волна, прошедшая сквозь границу II (сумма всех волн, проникших через эту границу).
Величины A, B, C, D, F выражают комплексные значения амплитуд электрических векторов соответствующих волн.
Радиопрозрачность слоя характеризуется двумя величинами:
коэффициентом отражения
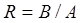(1.9)
и коэффициентом прохождения
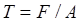. (1.10)
Оба коэффициента так же, как и напряженности A, B, F, являются, вообще говоря, комплексными.
Учитывая непрерывность касательных составляющих электрического и магнитного полей на границах сред воздух - диэлектрик, можно выразить комплексные амплитуды отраженной (B) и прошедшей сквозь слой (F) волн через комплексную амплитуду падающей волны (A) и затем с помощью соотношений (1.9) и (1.10) получить формулы для расчета коэффициентов R и T.
Если волна падает на слой под косым углом, то отраженную волну и волну, прошедшую сквозь слой, находят путем суммирования волн всех “порядков" B1, B2, …, а также соответственно F1, F2, … (рисунок 1.3, б).
Расчетные формулы для коэффициентов R и T имеют вид [22]
(1.11)
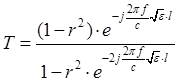, (1.12)
где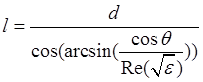 
. (1.13)
Здесь d - толщина слоя; f- частота; с = 3*108 - скорость света в вакууме; r - коэффициент отражения на границе сред воздух - диэлектрик.
Коэффициент отражения для поля вертикальной поляризации
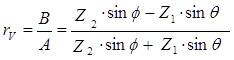. (1.14)
Коэффициент отражения для поля горизонтальной поляризации
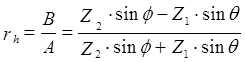
, (1.15)
где Zi - характеристическое сопротивление 1-й или 2-й среды.
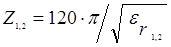. (1.16)
Если первая среда - свободное пространство (e1=1), а вторая среда не обладает магнитными свойствами (m1 = m0), то выражения (1.14), (1.15) упрощаются:
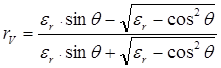, (1.17)
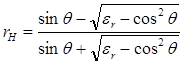. (1.18)
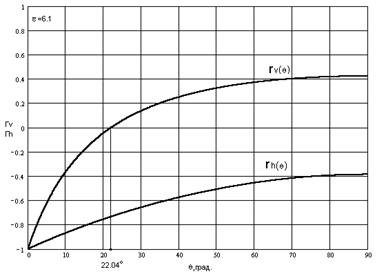
Рис.1.4 Зависимость коэффициента отражения волны вертикальной и горизонтальной поляризации от угла падения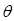 
, падающей на бетонную поверхность (er = 6.1)
Для углов падения, близких к скользящим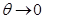 
, коэффициенты отражения 
; 
.
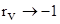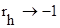Для некоторого угла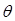 
коэффициент отражения для волны вертикальной поляризации 
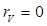. Этот угол называется углом Брюстера qБР (угол, для которого нет отраженной волны вертикальной поляризации):
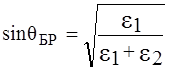. (1.19)
Если первая среда - воздух, а диэлектрическая проницаемость второй среды er, то
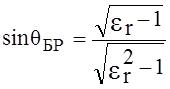. (1.20)
Угол Брюстера имеет место только для вертикальной поляризации поля. Коэффициент прохождения слоя можно представить в виде
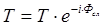. (1.21)
Если из аргумента Фсл вычесть запаздывание по фазе Ф0, существовавшее на отрезке, равном толщине слоя до его размещения на пути волны, то получим дополнительный сдвиг по фазе, вносимый слоем,
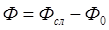, (1.22)
Где
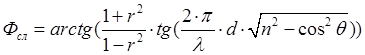, (1.23)
.
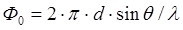Таким образом, диэлектрический слой влияет не только на амплитуду проходящей сквозь него волны, но и на фазу. [21]
Дифракция радиоволн
Явление дифракции позволяет радиоволнам распространяться вокруг сферической земной поверхности за горизонт и за различные препятствия. Несмотря на перекрытие прямой видимости и существенное уменьшение уровня сигнала, он все таки остается достаточным для приема.
Феномен дифракции объясняется принципом Гюйгенса - вторичного переизлучения точек фронта волны с различной фазой (зон Френеля). Напряженность поля определяется векторной суммой вклада вторичных излучателей.
Геометрия зон Френеля
Пусть между излучателем и приемником расположено препятствие - экран высотой h бесконечных размеров в поперечном сечении. Расстояние от экрана до излучателя - d1, до приемника - d2.
Рис.1.5 Дифракция радиоволн на клиновидном препятствии
Ясно, что путь через кромку препятствия больше прямого. Полагая, что h<<d1,d2 и h>>l, разность хода прямого и через кромку лучей будет:
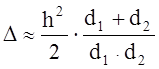. (1.27)
Соответствующая ему разность фаз
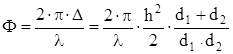, (1.28)
где используется приближение для малого аргумента tg x » x, а угол a аппроксимирован выражением
.
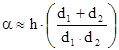Выражение (1.28) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля - Кирхгофа:
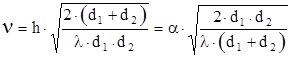, (1.29)
где a подставляется в радианах, все остальные параметры - в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения
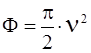. (1.30)
Из выражения (1.30) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.
Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nl/2 по сравнению с прямым лучом (l - длина волны, n - целое число).
В мобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.
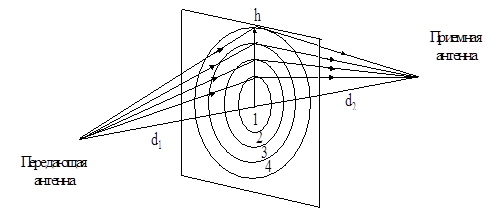
Рис.1.6 Формирование зон Френеля
Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.
Дата: 2019-07-30, просмотров: 742.
