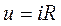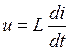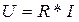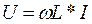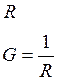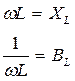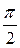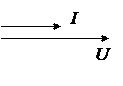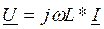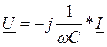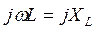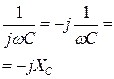Цель и содержание

Цель работы: Экспериментально исследовать режимы работы неразветвленной цепи переменного тока, содержащей R, L и С элементы, в том числе режим «резонанса напряжений».

    Содержание работы:

1. Экспериментально исследовать режимы работы неразветвленной цепи переменного тока, содержащей активные и реактивные потребители.

2. Экспериментально изучить явление «резонанса напряжений».

Теоретическое обоснование

Электрические цепи, в которых ЭДС, напряжения и токи изменяются во времени по синусоидальному закону, называются цепями переменного синусоидального тока. Элементами схем замещения цепей синусоидального тока являются источники синусоидального тока, источники синусоидальной ЭДС, активное сопротивление, индуктивный и емкостной элементы.

Термин «сопротивление» для цепей синусоидального тока включает в себя резистивные элементы, в которых выделяется энергия в виде тепла (активные сопротивления), и элементы, в которых энергия запасается в электрическом и магнитном полях. Сопротивления таких элементов называются реактивными. Реактивными сопротивлениями обладают индуктивный (Х_L=ωL) и емкостный ( 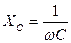) элементы. Отсюда, модуль полного сопротивления цепи синусоидального тока определяется выражением

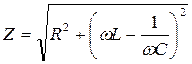.                               (6)

Эквивалентные преобразования в электрических цепях синусоидального тока аналогичны цепям постоянного тока и для исследуемой в работе схемы с последовательным соединением элементов величина протекающего тока будет одинакова во всех элементах, а напряжение на зажимах цепи (рисунок 3) определяться суммой падений напряжений на каждом из элементов

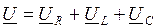.                            (7)

Реактивные элементы исследуемой цепи можно представить их схемами замещения:

а) любая реальная катушка (обмотка) обладает индуктивностью L и активным сопротивлением R, поэтому ее представляют в виде последовательно соединенных индуктивности и сопротивления ;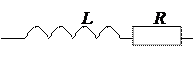

б) если диэлектрик, разделяющий пластины конденсатора, идеальный

(без потерь энергии) или конденсатор вакуумный, то схемой замещения такого конденсатора является изображение емкости. Но если требуется учесть потери энергии в реальном конденсаторе, заполненном диэлектриком, то составляют схему замещения конденсатора, где параллельно емкости включают активное сопротивление, которое имитирует потери энергии в реальном диэлектрике.

Фазовые соотношения между током и напряжением на резистивном, индуктивном и емкостном элементах цепи синусоидального тока приведены в таблице 4.

В качестве критерия режима «резонанс» в электрических цепях, содержащих катушки индуктивности и конденсаторы, принимается совпадение по фазе тока и напряжения на входных зажимах, т.е. фазовый резонанс.

Таблица 4 – Фазовые соотношения на элементах схемы

Характеристика	Связи между напряжениями и токами на элементах
			u
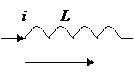
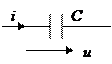
Во временной области
Компонентное уравнение
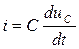
Действующие величины тока и напряжения
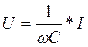
Сопротивление и проводимость
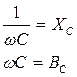
Угол сдвига фаз между напряжением и током	0
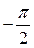
Векторные диаграммы напряжений и токов
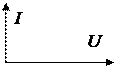
Комплексное представление
Комплексное действующее значение напряжения
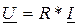
Комплексное сопротивление

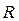
    Возможны два основных типа резонанса: при последовательном соединении катушки индуктивности и конденсатора – резонанс напряжений и при их параллельном соединении – резонанс токов. В данной лабораторной работе будет исследоваться явление «резонанса напряжений».

Резонанс напряжений возможен на неразветвленном участке электрической цепи, который содержит индуктивный L, емкостной С и резистивный R элементы, т.е. в последовательном колебательном контуре (рисунок 3).

Рисунок 3 – Схема последовательного контура

     По закону Ома комплексная величина тока определяется

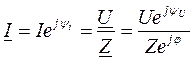,                              (8)

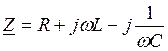где    и 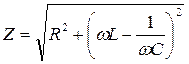- комплексное и полное сопротивления контура соответственно;

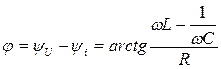      - угол сдвига фаз между напряжением и током, т.е. аргумент комплексного сопротивления;

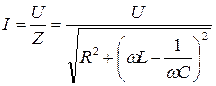  – действующее значение тока. (9)

     Режим работы неразветвленного участка цепи, при котором ее ток и напряжение совпадают по фазе 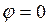, т.е. 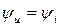, называется резонансом напряжений. При резонансе напряжений возникает равенство действующих значений напряжений на емкостном и индуктивном элементах, которые находятся в противофазе (см. векторную диаграмму рисунка 4).

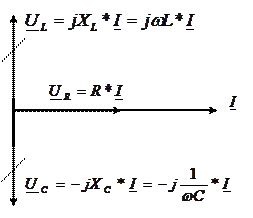
Рисунок 4 – Векторная диаграмма для режима резонанса напряжений

    Из вышеприведенных соотношений следует, что условие, при котором наблюдается резонанс, определяется равенством .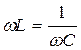

    Резонанса можно достичь, изменяя частоту приложенного к цепи напряжения или параметры цепи: индуктивность катушки или емкость конденсатора. При этом величины угловой частоты, индуктивности и емкости, при которых наступает резонанс, определяются формулами

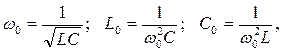                            (10)

где ω₀ - резонансная угловая частота.

    Если напряжение U на зажимах цепи и активное сопротивление R цепи не изменяются, то ток при резонансе имеет наибольшее значение, равное 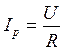 и не зависящее от величин реактивных сопротивлений. Отношение  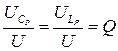 – добротность контура, которая определяет кратность превышения напряжения на зажимах индуктивного и емкостного элементов над напряжением на зажимах всей цепи (напряжением питания).

Практическое значение имеют зависимости действующих или амплитудных значений токов и напряжений от частоты для цепей, в которых возможен резонанс. Эти зависимости называются резонансными кривыми.

Между параметрами электрической цепи синусоидального тока существуют соотношения, необходимые при расчете данной лабораторной работы:

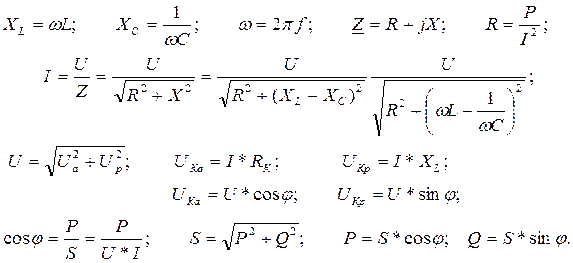(11)

Аппаратура и материалы

Для выполнения работы необходимы лабораторные стенды «Электротехника», включающие в себя:

– элементы, обладающие активными и реактивными сопротивлениями (катушку индуктивности, батарею конденсаторов и реостат);

– переносной ваттметр для измерения активной мощности;

– измерительные приборы переменного тока.