Заодно познакомимся со стандартным приёмом получения приближённых решений. Проблема такая опять. Имеем распределение заряда1), мы теперь попробуем получить более точную формулу, не так радикально, а, вот, если уйти достаточно далеко, но ещё, когда это распределение не выглядит совсем точечным, хотим получить более точное приближение. Пусть у нас L – характерный линейный размер системы, будем считать, что 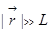 , это можно оформить иначе:
, это можно оформить иначе: 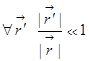 ,
, 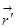 это в пределах распределения,
это в пределах распределения, 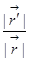 – это малая величина.
– это малая величина.
 А теперь вот чем займёмся:
А теперь вот чем займёмся: 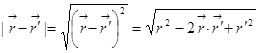 .
.
Стандартный приём: когда у вас имеется сумма, в которой одно слагаемое большое, а другие маленькие, то всегда есть смысл вынести большое слагаемое за скобку и получить в сумме единицу плюс какие-то маленькие добавки, которая разлагается в ряд.
Пишем дальше: 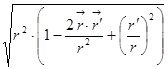 2)
2) 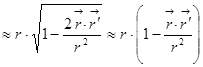 . Мы избавились от корня, ну, потому что
. Мы избавились от корня, ну, потому что 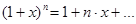 . А теперь, добывши этот результат, займёмся формулой для потенциала:
. А теперь, добывши этот результат, займёмся формулой для потенциала: 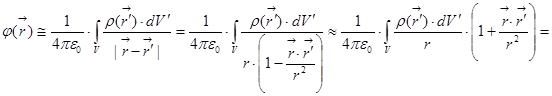
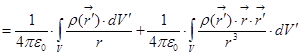 3)
3) 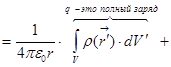 +
+ 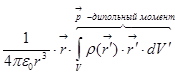 . Тогда мы получаем такую формулу для потенциала:
. Тогда мы получаем такую формулу для потенциала:
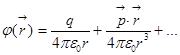 .
.
Если бы мы произвели разложение поля в точке, вот я там выкинул 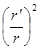 , если ещё взять следующие поправки, то тут пошло бы слагаемое, которое характеризовало бы не дипольный момент, а, так называемый, квадрупольный момент и дальше моменты более высоких порядков. Вот сама такая процедура называется разложением по мультиполям. Мультиполь нулевого порядкам – это просто заряд, дальше, мультиполь первого порядка – это дипольный момент, дальше там квадрупольный момент. Дипольный момент задаётся вектором, квадрупольный бы момент задавался квадратной матрицей из девяти элементов, но вследствие симметрии там было бы только шесть отличных от нуля и так далее.
, если ещё взять следующие поправки, то тут пошло бы слагаемое, которое характеризовало бы не дипольный момент, а, так называемый, квадрупольный момент и дальше моменты более высоких порядков. Вот сама такая процедура называется разложением по мультиполям. Мультиполь нулевого порядкам – это просто заряд, дальше, мультиполь первого порядка – это дипольный момент, дальше там квадрупольный момент. Дипольный момент задаётся вектором, квадрупольный бы момент задавался квадратной матрицей из девяти элементов, но вследствие симметрии там было бы только шесть отличных от нуля и так далее.
Это мы нашли потенциал, ну, а теперь поупражняемся в нахождении напряжённости. 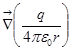 – это даст напряжённость поля точечного заряда, вычислим
– это даст напряжённость поля точечного заряда, вычислим 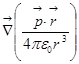 .
. 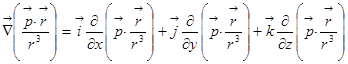 =
= 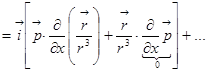 1)=
1)= 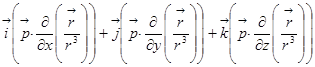 =
= 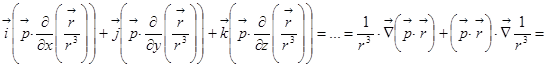
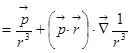 2) =
2) = 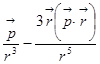 .
.
Тогда для напряжённости поля получаем:
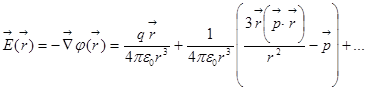 .
.
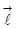

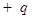
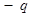
 Поле диполя.
Поле диполя.
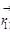 Диполем называется такое распределение заряда, для которого полный заряд равен нулю, однако дипольный момент не равен нулю:
Диполем называется такое распределение заряда, для которого полный заряд равен нулю, однако дипольный момент не равен нулю: 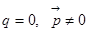 . Легко предъявить такое распределение. Пусть мы имеем два одинаковых точечных заряда, но противоположных знаков.
. Легко предъявить такое распределение. Пусть мы имеем два одинаковых точечных заряда, но противоположных знаков.  . Дипольный момент у нас был определён:
. Дипольный момент у нас был определён: 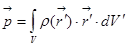 . это что означает? заряд в маленьком элементе объёма dq умножается на радиус-вектор и суммируется по всем зарядам, если записать это дело через сумму, то это будет так:
. это что означает? заряд в маленьком элементе объёма dq умножается на радиус-вектор и суммируется по всем зарядам, если записать это дело через сумму, то это будет так: 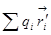 . Вот этот интеграл, если представить всё это как совокупность точечных зарядов, изображается вот такой суммой, каждый заряд умножается на свой радиус-вектор и всё складывается.
. Вот этот интеграл, если представить всё это как совокупность точечных зарядов, изображается вот такой суммой, каждый заряд умножается на свой радиус-вектор и всё складывается.
Между прочим, в механике, если мы брали бы массу частицы, умножали на радиус-вектор и суммировали, чтобы мы получили? Мы получили бы массу системы умноженную на радиус-вектор центра масс. Если начало координат выбрать в центре масс системы, то «дипольный момент – распределение масс» всегда равнялся бы нулю. Электрический заряд имеет разные знаки, здесь ситуация другая.
Значит, дипольный момент для нашей системы равняется: 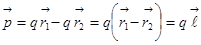 . Дипольный момент двух одинаковых по величине и противоположных по знаку зарядов – это вектор, идущий из отрицательного заряда в положительный, умноженный на заряд.
. Дипольный момент двух одинаковых по величине и противоположных по знаку зарядов – это вектор, идущий из отрицательного заряда в положительный, умноженный на заряд.
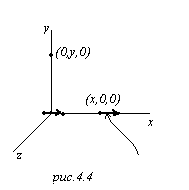
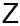

 Теперь найдём электрическое поле. Пусть дипольный момент, вектор
Теперь найдём электрическое поле. Пусть дипольный момент, вектор 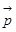 , в начале координат ориентирован вдоль оси ОХ,
, в начале координат ориентирован вдоль оси ОХ, 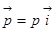 . Вычислим поле в точке (х,0,0).
. Вычислим поле в точке (х,0,0).
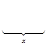
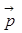
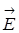
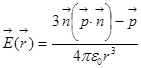 , где
, где 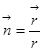 .
.
Тогда 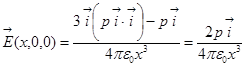 .
.
Мораль такая: на оси ОХ напряжённость поля убывает как 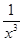 , то есть она обратно пропорциональна кубу расстояния, от точечного заряда – обратно пропорциональна квадрату расстояния. Направление вектора
, то есть она обратно пропорциональна кубу расстояния, от точечного заряда – обратно пропорциональна квадрату расстояния. Направление вектора 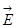 в точке (х,0,0) задаётся направлением вектора
в точке (х,0,0) задаётся направлением вектора 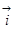 , то есть напряжённость направлен вдоль оси ОХ.
, то есть напряжённость направлен вдоль оси ОХ.
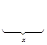
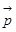
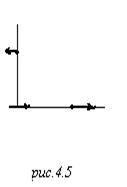 Теперь возьмём точку (0,у,0).
Теперь возьмём точку (0,у,0). 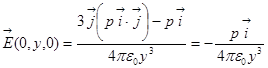 . Это что означает? Что для этого диполя вектор
. Это что означает? Что для этого диполя вектор 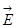 в точке (х,0,0) такой, а здесь в точке (0,у,0) вектор -
в точке (х,0,0) такой, а здесь в точке (0,у,0) вектор - 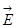 и по величине в два раза меньше, на том же самом расстоянии, х=у.
и по величине в два раза меньше, на том же самом расстоянии, х=у.
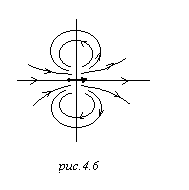 |
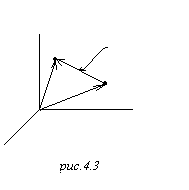
Электрический диполь, ориентированный таким образом, создаёт поле с такими силовыми линиями:
Вот такую структуру имеет поле диполя.
Многие молекулы обладают дипольным моментом, и с этим связаны свойства вещества, которые мы рассмотрим в следующий раз.
5
Дата: 2019-07-24, просмотров: 278.