Магнитный момент сам создаёт поле, сейчас мы собственное его поле не рассматриваем, а нас интересует, как ведёт себя магнитный момент, помещённый во внешнее магнитное поле. На магнитный момент действует момент силы, равный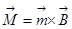 
. Момент силы будет направлен перпендикулярно к доске, и этот момент будет стремиться развернуть магнитный момент вдоль силовой линии. Почему стрелка компаса показывает на северный полюс? Ей, конечно, нет дела до географического полюса Земли, стрелка компаса ориентируется вдоль силовой линии магнитного поля, которая, в силу случайных причин, кстати, направлена примерно по меридиану. За счёт чего? А на неё действует момент. Когда стрелка, магнитный момент, совпадающий по направлению с самой стрелкой, не совпадает с силовой линией, появляется момент, разворачивающий её вдоль этой линии. Откуда у стрелки компаса берётся магнитный момент, это мы ещё обсудим.
Кроме того, на магнитный момент действует сила 
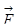, равная 
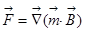. Если магнитный момент направлен вдоль 
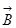, то сила втягивает магнитный момент в область с большей индукцией. Эти формулы похожи на то, как действует электрическое поле на дипольный момент, там тоже дипольный момент ориентируется вдоль поля и втягивается в область с большей напряжённостью. Теперь мы можем рассмотреть вопрос о магнитном поле в веществе.
Магнитное поле в веществе
 |
Атомы могут обладать магнитными моментами. Магнитные моменты атомов связаны с моментом импульса электронов. Уже была получена формула
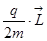, где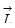 
– момент импульса частицы создающей ток. В атоме мы имеем положительное ядро и электрон е, вращающийся по орбите, на самом деле, в своё время мы увидим, что эта картина не имеет отношения к реальности, так нельзя представлять электрон, который вращается, но остаётся то, что электрон в атоме обладает моментом импульса, и этому моменту импульса будет отвечать такой магнитный момент: 
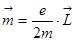. Наглядно, заряд, вращающийся по окружности, эквивалентен круговому току, то есть это элементарный виток с током. Момент импульса электрона в атоме квантуется, то есть может принимать только определённые значения, вот по такому рецепту: 
, 
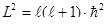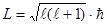, где вот эта величина 
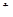– это постоянная Планка. Момент импульса электрона в атоме может принимать лишь определённые значения, мы сейчас не будем обсуждать, как это получается. Ну, и вследствие этого магнитный момент атома может принимать определённые значения. Эти детали нас сейчас не волнуют, но, по крайней мере, будем представлять, что атом может обладать определённым магнитным моментом, есть атомы, у которых нет магнитного момента. Тогда вещество, помещённое во внешнее поле намагничивается, а это означает, что оно приобретает определённый магнитный момент вследствие того, что магнитные моменты атомов ориентируются преимущественно вдоль поля.
Элемент объёма dV приобретает магнитный момент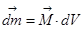 
, при чём вектор 
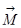имеет смысл плотности магнитного момента и называется вектором намагничивания. Имеется класс веществ, называемых парамагнетики, для которых 
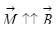, намагничивается так, что магнитный момент совпадает с направлением магнитного поля. Имеются диамагнетики, которые намагничиваются, так сказать, «против шерсти», то есть магнитный момент антипараллелен вектору 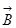, значит, 
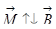. Это более тонкий термин. То, что вектор 
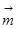параллелен вектору 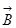понятно, магнитный момент атома ориентируется вдоль магнитного поля. Диамагнетизм связан с другим: если атом не обладает магнитным моментом, то во внешнем магнитном поле он приобретает магнитный момент, при чём магнитный момент антипараллелен 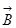. Этот очень тонкий эффект связан с тем, что магнитное поле влияет на плоскости орбит электронов, то есть оно влияет на поведение момента импульса. Парамагнетик втягивается в магнитное поле, диамагнетик выталкивается. Вот, чтобы это не было беспредметно, медь – это диамагнетик, и алюминий – парамагнетик, если взять магнит то алюминиевая лепёшка будет притягиваться магнитом, а тогда медная будет отталкиваться.
Понятно, что результирующее поле, когда вещество внесено в магнитное поле, это есть сумма внешнего поля и поля, создаваемого за счёт магнитного момента вещества. Теперь обратимся к уравнению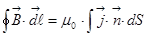 
, или в дифференциальной форме 
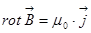. Теперь такое утверждение: намагничивание вещества эквивалентно наведению в нём тока с плотностью 
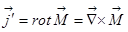. Тогда это уравнение мы напишем в виде 
.
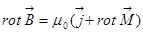Проверим размерность: М – это магнитный момент в единице объёма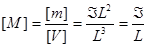 
, размерность 
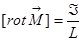. Когда вы пишете какую-нибудь формулу, то размерность всегда полезно проверять, особенно если формула эта собственной выводки, то есть вы её не срисовали, не запомнили, а получили.
9
Намагниченность характеризуется вектором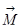 
, он так и называется вектор намагниченности, это плотность магнитного момента или магнитный момент в единицу времени. Я говорил, что намагниченность эквивалентна появлению тока 
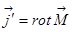, так называемого молекулярного тока, и это уравнение эквивалентно такому: 
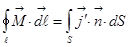, то есть мы можем считать, что нет намагниченности, а есть такие токи. Зададимся таким уравнением: 
, 
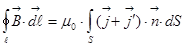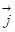- это настоящие токи, связанные с конкретными носителями зарядов, а 
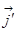это токи, связанные с намагниченностью. Электрон в атоме это круговой ток, возьмём область внутри, внутри образца все эти токи уничтожаются, но наличие таких круговых токов эквивалентно одному общему току, который обтекает этот проводник по поверхности, отсюда и такая формула. Перепишем это уравнение в таком виде: 
, 
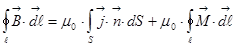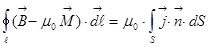. Этот 
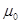тоже отправим влево и обозначим 
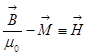, вектор 
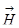называется напряжённостью магнитного поля, тогда уравнение приобретёт вид 
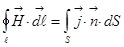. (циркуляция напряжённости магнитного поля по замкнутому контуру) = (сила тока через поверхность этого контура).
Ну, и, наконец, последнее. Мы имеем такую формулу: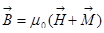 
. Для многих сред намагниченность зависит от напряжённости поля, 
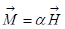, где 
– магнитная восприимчивость, это коэффициент, характеризующий склонность вещества к намагничиванию. Тогда эта формула перепишется в виде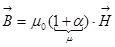 
, 
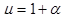– магнитная проницаемость, и мы получаем такую формулу: 
.
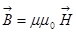Если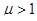 
, то это парамагнетики, 
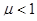- это диамагнетики, ну, и, наконец, имеются вещества, для которых это 
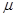принимает большие значения (порядка 103), 
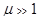- это ферромагнетики (железо, кобальт и никель). Ферромагнетики замечательны тем. Что они не только намагничиваются в магнитном поле, а им свойственно остаточное намагничивание, если он уже однажды был намагничен, то, если убрать внешнее поле, то он останется намагниченным в отличии от диа- и парамагнетиков. Постоянный магнит – это и есть ферромагнетик, который без внешнего поля намагничен сам по себе. Кстати, имеются аналоги этого дела в электричестве: имеются диэлектрики, которые поляризованы сами по себе без всякого внешнего поля. При наличии вещества наше фундаментальное уравнение приобретает такой вид:
,
,
.
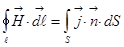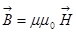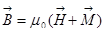А вот ещё пример ферромагнетика, бытовой пример магнитного поля в средах, во-первых, постоянный магнит, ну, и более тонкая вещь – магнитофонная лента. Каков принцип записи на ленту? Магнитофонная лента - это тонкая лента, покрытая слоем ферромагнетика, записывающая головка - это катушка с сердечником, по которой течёт переменный ток, в зазоре создаётся переменное магнитное поле, ток отслеживает звуковой сигнал, колебания с определённой частотой. Соответственно, в контуре магнита имеется переменное магнитное поле, которое меняется вместе с этим самым током. Ферромагнетик намагничивается переменным током. Когда эта лента протягивается по устройству такого типа, переменное магнитное поле создаёт переменную э.д.с. и воспроизводится опять электрический сигнал. Это ферромагнетики на бытовом уровне.
Квазистационарные поля
Приставке «квази-» русский эквивалент «якобы», то есть имеется в виду, что поле переменное, но не очень. Теперь мы полагаем, наконец,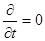 
, но оставим одно: 
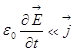, чтобы не учитывать влияния электрического поля на магнитное. Уравнения Максвелла приобретают такой вид:
1) 
,
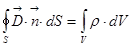2) 
,
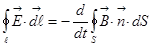3) 
,
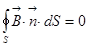4) 
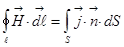
3) и 4) уравнения не изменились, это означает, что связь магнитного поля с токами в каждой точке осталась такой же, только мы теперь допускаем изменяющиеся со временем токи. Ток со временем может меняться, но связь магнитного поля и тока остаётся та же самая. Поскольку магнитная индукция связана с током линейно, будет меняться синхронно с током проводника: ток нарастает, магнитное поле нарастает, но связь между ними не меняется. А вот для электрического поля появляется новшество: циркуляция связана с изменением магнитного поля.
Дата: 2019-07-24, просмотров: 164.
