Предшествующих вершин

Доказательство с отфильтровыванием предшествующих вершин производится с использованием AF-графа. Граф опровержения имеет AF-форму, если каждая из его вершин соответствует одному из следующих предложений:

1. базовому предложению;

2. предложению, непосредственно следующему за базовым;

3. предложению, непосредственно следующему за двумя небазовыми предложениями A и B, из которых B предшествует A (отсюда термин отфильтровывание предшествующих вершин).

Граф в виде лозы представляет собой частный случай графа в AF-форме: каждая из его вершин соответствует либо предложению 1, либо предложению 2. Но граф типа лозы существует не для всех неудовлетворимых множеств. Ниже приведен пример такого графа.[2]

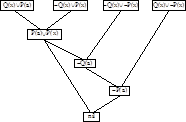
Рис 1.1. Вид графа в AF-форме.

Стратегии поддерживающего множества

Стратегией поддерживающего множества называют стратегию, в которой выбирается такое непустое множество K исходного множества предложений S, что множество S-K удовлетворимо. Например, в качестве K можно взять множество предложений, возникающих из отрицания доказываемой теоремы. Говорят, что предложения в K имеют поддержку. При поиске опровержения допустимыми считаются резольвенты лишь тех пар предложений, в которых, по крайней мере, одно имеет поддержку, каждому предложению, построенному в результате резольвенции, также придается поддержка.

Так как множество S-K удовлетворимо, существует граф опровержения, имеющий AF-форму, у которого верхней вершиной служит один из элементов множества K. Таким образом, стратегия поддерживающего множества полна, поскольку она допускает все резольвенции, допускаемые AF-стратегией.[2]

Стратегии упорядочения

На основе резольвенций, обеспечиваемых различными стратегиями очищения, иногда можно искать опровержение, упорядочив выполняемые резольвенции. В стратегиях упорядочения не запрещаются никакие типы резольвенций, а лишь даются указания на то, какие из них надо выполнять в первую очередь. Стратегии упорядочения соответствуют эвристическим стратегиям перебора для поиска на графах. При хорошем упорядочении не обязательно вычислять все элементы множеств R(S), R²(S) и т.д. Если пустое предложение появляется впервые на уровне n, что хочется думать, можно прямо направить на этот уровень, не заполняя нижние уровни.

Две довольно эффективные стратегии упорядочения – это стратегия предпочтения одночленам и стратегия наименьшего числа компонент. В стратегии предпочтения одночленам делается попытка сначала построить резольвенты между одночленами, т.е. предложениями, содержащими один литерал. Если это удается, то сразу же получается опровержение. Если же не могут найти пару одночленов, у которых есть резольвента, то пытаются найти резольвенту для пар одночлен-двучлен и т.д. Как только какая-нибудь пара предложений разрешается, полученную резольвенту сразу сопоставляют с одночленами с тем, чтобы найти возможные резольвенты. Во избежание совершения невыгодной цепочки одночленных резольвенций обычно устанавливается граничный уровень.

Стратегия предпочтения одночленам оправдана гарантированным укорочением длины предложений, вызываемым одночленными резольвентами. Так как цель построения резольвент состоит в образовании пустого предложения, то стратегия предпочтения одночленам напрашивается сама собой. При введении граничных уровней для возможности использования и других резольвенций такая стратегия не препятствует нахождению опровержения и, как правило, сильно ускоряет процесс перебора.

Стратегия наименьшего числа компонент упорядочивает резольвенции согласно длине получаемых резольвент. Так, два предложения, дающие наиболее короткую резольвенту, разрешаются в первую очередь. Эта стратегия в некотором смысле дороже, поскольку до выполнения резольвенции надо подсчитать длины потенциальных резольвент и упорядочить их.[2]