Для автоматического анализа рассуждений необходим некоторый формальный язык, на котором можно формировать посылки и делать верные выводы. Все, что для этого требуется, - это возможность описать интересующую нас задачу и средства поиска соответствующих шагов в процессе логического вывода.

Исчисление предикатов первого порядка – это такая система в логике, в которой можно выразить большую часть того, что относится к математике, а также многое из разговорного языка. Эта система содержит правила логического вывода, позволяющие делать верные логические построения новых утверждений. Благодаря своей общности и логической силе исчисление предикатов может всерьез претендовать на использование его для машинного построения умозаключений.

Язык, подобный языку в исчислении предикатов, определяется его синтаксисом. Чтобы задать синтаксис, надо задать алфавит символов, которые будут использоваться в этом языке. Один из важных классов выражений в исчислении предикатов – это класс правильно построенных формул.

Мы обычно пользуемся языком для того, чтобы делать утверждения, касающиеся интересующей нас области. Отношения между языком и описываемой им областью определяется семантикой этого языка. Правильно построенные формулы исчисления предикатов как раз являются теми выражениями, которые мы будем использовать в качестве утверждений, касающихся интересующей нас области. Говорят, что правильно построенные формулы принимают значения T или F в зависимости от того, являются эти утверждения в этой области истинными или ложными. Приемы обращения с правильно построенными формулами позволяют строить умозаключения, относящиеся к некоторой области, и, следовательно, могут представить интерес при создании принятия решения, требующего такого умозаключения.[2]

Унификация и принцип резольвенции в исчислении

Предикатов

Унификация – процесс, являющийся основным в формальных преобразованиях, выполняемых при нахождении резольвент.

Термы литерала могут быть переменными буквами, константными буквами и выражениями, состоящими из функциональных букв и термов. Подстановочный частный случай литерала получается при подстановке в литералы термов вместо переменных. Например, для литерала 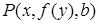 частными случаями будут , , , .

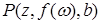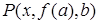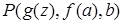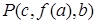Первый частный случай называется алфавитным вариантом исходного литерала, поскольку здесь вместо переменных, входящих в 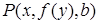, подставлены лишь частные переменные. Последний из четырех частных случаев называется константным частным случаем, или атомом, так как ни в одном из термов этого литерала нет переменных.

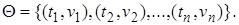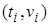В общем случае любую подстановку можно представить в виде множества упорядоченных пар  Пара  означает, что повсюду переменная  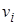заменяется термом 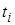. Существенно, что переменная в каждом ее вхождении заменяется одним и тем же термом. Для получения частных случаев литерала  были использованы четыре подстановки

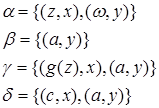
Обозначим через 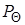 частный случай литерала P, получающийся при использовании подстановки 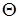. Например, 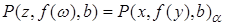. Композицией  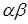двух подстановок  и  называется результат применения 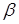 к термам подстановки  с последующим добавлением пар из , содержащие переменные, не входящие в число переменных из . Можно показать, что применение к литералу P последовательно подстановок  и  дает тот же результат, что и применение подстановки 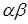, то есть . Можно также показать, что композиция подстановок ассоциативна: 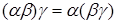. Если подстановка  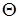применяется к каждому элементу множества  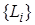литералов, то множество соответствующих ей частных случаев обозначается через 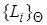. Множество  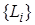литералов называется унифицируемым, если существует такая подстановка 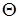, что 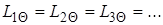. В этом случае подстановку  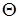называют унификатором 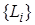, поскольку ее применение сжимает множество до одного элемента. Наиболее общим (или простейшим) унификатором для  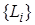будет такой унификатор 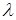, что если  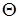- какой-нибудь унификатор для 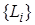, дающий 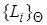, то найдется подстановка , для которой .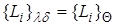

Существует алгоритм, называемый алгоритмом унификации, который приводит к наиболее общему унификатору для унифицируемого множества 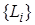 литералов и сообщает о неудаче, если множество неунифицируемо. Алгоритм начинает работу с пустой подстановки и шаг за шагом строит наиболее общий унификатор, если такой существует.

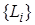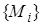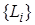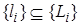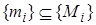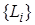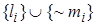Пусть исходные предложения задаются в виде  и  и переменные, входящие в , не встречаются в  и обратно. Пусть  и  - такие два подмножества  и , что для объединения  существует наиболее общий унификатор 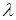. Тогда говорят, что два предложения  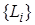и 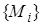 разрешаются, а новое предложение  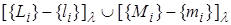является их резольвентой. Резольвента представляет выведенное предложение, и процесс образования резольвенты из двух "родительских" предложений называется резольвенцией.

Иными словами мы хотим иметь возможность находить доказательство того, что некоторая правильно построенная формула W в исчислении предикатов логически следует из некоторого множества S правильно построенных формул. Это задача эквивалентна задаче доказательства того, что множество 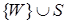 неудовлетворимо. Процессы выявления неудовлетворимости некоторого множества предложений называются процессами опровержения.

Принцип резольвенции непротиворечив и полон. Непротиворечивость означает, что если когда-нибудь мы придем к пустому предложению, то исходное множество обязано быть неудовлетворимым. Полнота означает, что если исходное множество неудовлетворимо, то, в конце концов, мы придем к пустому предложению.[2]