Эффект Холла заключается в возникновении поперечного электрического поля εн в кристалле, по которому протекает ток I, при помещении его во внешнее магнитное поле Во, перпендикулярное I (рис. 1.1). Поле Six перпендикулярно I и Во, а его напряженность пропорциональна току и индукции магнитного поля.

Рассмотрим движение электронов на примере рис. 1.1. Под действием электрического поля они движутся справа налево, однако сила Лоренца
Fл = -e[vдрB0] смещает их к передней стенке образца, создавая тем самым поперечный градиент заряда и связанное с ним электрическое поле εн . Поперечное поле εн в свою очередь ограничивает приток электронов к передней стенке, и в состоянии равновесия сила, с которой оно воздействует на электрон, равна отклоняющей силе Лоренца:

-е εн = evдрB0 (1.1)

Отсюда

εн = - vдр B0           (1.2)

Теперь уже вектор тока I, направление которого не изменилось, не параллелен вектору суммарного электрического поля ε + εн. Угол между ними, называемый углом Холла Он, определяется равенством

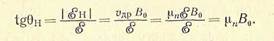(1.3)

Ток в поперечном сечении образца S

I = js — jbd        (1.4)

Учитывая, что j = envдр , можно получить выражение для поперечной разности потенциалов (э.д.с. Холла):

VH=b εн = - b (i/en) B0 = - b (I/bd)(B0/en) = - (1/en)(IB0/d) (1.4)

При выводе формулы (1.4) предполагалось, что все электроны имеют одинаковые дрейфовые скорости, и не учитывался механизм их рассеяния в кристалле. Более строгое выражение для э.д.с. Холла с учетом распределения электронов по скоростям и связанного с этим: изменения времени релаксации записывается в виде

VH = - (A/en)(IB0/d) (1.5)

или, если ввести постоянную Холла RH = - A/(en),

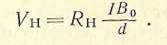 (1.6)

Константа А определяется механизмом рассеяния электронов:

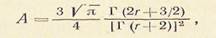 (1.7)

где r — имеет то же значение, что и в (9.58); Г — гамма-функция.

В атомных кристаллах A = 1.18, в решетках с ионизированными примесями A = 1.93, в металлах и сильно вырожденных полупроводниках, у которых в электропроводности участвуют лишь, электроны с энергией, близкой к EF, т. е. имеющие практически одинаковые скорости, А = 1.

Величина |Rn| не зависит от индукции магнитного поля и лишь в очень сильных полях уменьшается от А/(пе) до 1/(пе) при любом механизме рассеяния. У металлов RH имеет порядок 10-10 м3/Кл, у полупроводниковых соединений она возрастает вплоть до 102 м3/Кл (Si). Аномально большие значения постоянной Холла у металлов V группы (Bi, Sb, Аs)—до 106 м3/Кл.

Электроны и дырки отклоняются при тех же направлениях векторов I и В0, к одной и той же грани образца, поэтому в дырочном; и; электронном полупроводниках направления εн противоположны. Постоянную Холла Rn принято считать отрицательной при электронном типе электропроводности и положительной — при дырочном. В частности, постоянная Холла положительна у ряда: металлов, например Cd, Zn. Это объясняется тем, что зона проводимости подобных веществ заполнена почти полностью и оставшиеся незаполненные уровни ведут себя как положительные заряды — дырки. При наличии носителей зарядов обоих знаков

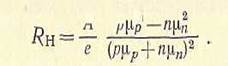 (1.8)

В зависимости от концентрации и подвижности носителей заряда Rn, как следует из (1.8), может быть больше или меньше нуля. В собственном полупроводнике п = р и

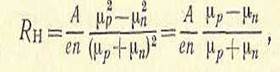 (1.9)

так что при mp = mn , RH = 0. Для веществ с одним типом носителей заряда o = enm, и |Rn| = A/en, следовательно, измерив постоянную Холла и проводимость, можно найти подвижность носителей заряда:

m = (o |RH|)/A (1.10)

Таким образом, исследования эффекта Холла позволяют составить представление о знаке и концентрации носителей заряда в веществе. Из анализа температурной зависимости RH можно получить сведения о ширине запрещенной зоны и структуре примесных уровней, а измерения o дают возможность найти также подвижность носителей заряда.

В выражении для силы Лоренца мы пренебрегли тепловой составляющей скорости и считали, что все электроны обладают одинаковой средней скоростью. В этом предположении выведено условие равенства сил электрического и магнитного полей (1.1). Однако реальный электронный газ в кристалле имеет некоторое распределение по скоростям и условие (1.1) выполняется лишь для небольшой части электронов. На более быстрые электроны действует большая отклоняющая сила магнитного поля, и они могут преодолеть силы поперечного электрического поля Холла. Медленные же электроны, на которые действует меньшая отклоняющая сила Лоренца, не могут преодолеть силу еεн и смещаются к противоположной стенке образца. В результате происходит разделение электронов в поперечном направлении в зависимости от значения их скорости, и вследствие обмена энергией электронов с решеткой (быстрые электроны отдают энергию, а медленные увеличивают ее за счет решетки) в поперечном направлении появляется градиент температуры (аффект Эттингсгаузена) VT = P[IВ0], где
Р — коэффициент Эттингсгаузена. Поперечный перепад температур невелик— обычно он не превышает долей градуса.

Помещение вещества в магнитное поле изменяет продольную компоненту проводимости. Это явление называют магнетосопротивлением (магниторезистивным эффектом, эффектом Гаусса). Магнитное поле вызывает искривление траекторий электронов проводимости, и если вдоль искривленной траектории длина свободного пробега останется прежней, то в направлении электрического поля она уменьшится, а следовательно, уменьшится и проводимость. Можно показать, что изменение проводимости связано с величиной магнитного поля и подвижностью носителей заряда соотношением

Δo /o = - C(mnB0)2 (1.11)

Как видно из формулы (1.11), магнетосопротивление в отличие от эффекта Холла является четной функцией относительно магнитного поля — изменение направления вектора Во на противоположное не влияет на Да. Коэффициент С определяется механизмом рассеяния носителей заряда и равен (9/16)π я для атомных и (27/64)π я для ионных кристаллов. Для примесных полупроводников С = π /10 в атомных решетках и С = 0,96 — в ионных. Измеряя зависимость Δo /o от величины магнитного поля, можно определить подвижность носителей заряда.

Значения Δo /o для металлов невелики, однако у висмута это отношение может достигать 200% и по его изменению можно измерять магнитные поля. Для полупроводников отношение Δo /o изменяется в широких пределах в зависимости от их типа (от средних значений 10-2 – 10-1 до нескольких единиц). В полях напряженностью выше 106 А/м зависимость Δo /o от В0 отклоняется от квадратичной и Δo /o ~ Вm0, где 1 < m < 2.

Распределение электронов по скоростям сказывается на степени их смещения магнитным полем. Медленные электроны сильнее «закручиваются» и не могут пройти вдоль всего образца в отличие от более быстрых электронов, тем самым создается продольный градиент температуры ∂Т/∂х ~ В20y Ix (эффект Нернста).

Гальваномагнитные эффекты широко используют в установках для лабораторных исследований и в ряде технических устройств. Сюда следует отнести, прежде всего, измерения параметров электронного газа, о которых упоминалось ранее. Широкое применение нашел эффект Холла в устройствах для измерения напряженности постоянного и переменного (до 1012 Гц) магнитных полей (магнитометры), силы тока (по создаваемому им магнитному полю), электрической мощности (ваттметры) и т. д., а также в некоторых преобразовательных устройствах. В качестве датчиков Холла используют различные полупроводниковые соединения с большими (10-5 - 102 м3/Кл) значениями RH — Ge, Si, InAs, InSb, HgSe, HgTe, Cd3As2, InAsP и др. Ведутся исследования по созданию охлаждающих устройств на основе эффекта Эттингсгаузена и уже получены перепады температуры до 100°.