Теоретичні основи розрахунку являються загальними для всіх типів ременів. Основними критеріями працездатності ременних передач є: тягова здатність, яка визначається силою тертя між та шківом, довговічність ременя, яка в умовах нормальної експлуатації обмежується розрухою ременя від втоми. На сьогоднішній день основними розрахунками ременних передач є розрахунки по тяговій здатності. Довговічність ременя збільшують при розрахунку шляхом вибору основних параметрів передачі в співвідношенні з рекомендаціями, виробленими на практиці.
1.3.1. Кінематичні параметри. Окружні швидкості на шківах
v1 = d1 n1 / 60 ; v2 = d2 n2 / 60. (1.1)
Враховуючи жорстке ковзання ременя, можна записати v1 < v2 чи
v2 = v1 (1—ε). (1.2)
де ε – коефіцієнт ковзання. При цьому передаточне відношення
i = n1 / n2 = v1 d1 = d2 / [ d1 (1—ε) ]. (1.3)
В подальшому показано, що величина ε залежить від навантаження, тому в ременній передачі передаточне відношення не завжди є постійним. При нормальних робочих нагрузках ε ≈ 0,01…0,02. Найбільше значення ε дозволяє наближено приймати:
i ≈ d2 / d1. (1.4)
1.3.2 Геометричні параметри
На рис1.7, а – міжосьова відстань; β – кут між гілками ременя; α – кут обхвату ременем малого шківа. При геометричному розрахунку відомими зазвичай є d1, d2 і а, які визначають кут і довжину ременя l. В результаті витяжки і провисання ременя значення α і l не являються точними і визначаються приблизно так:
α = 180°— β ; sin (β/2) = (d2— d1) / (2a) (1.5)
Враховуючи, що β/2 практично не перевищує 15°, приблизно приймаємо значення синуса рівним аргументу і запишемо
β = (d2 — d1) / а рад ≈ 57 ( — d1) / а° (1.6)
Довжина ременя вираховується як сума прямолінійних ділянок і дуг обхвату:
l ≈ 2a + 0,5 (d2 + d1) / (4а) (1.7)
 |
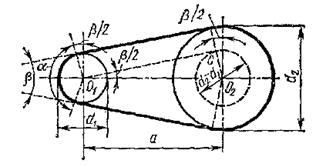Рис. 1.7 Геометричні параметри передачі
1.3.3 Сили та силові залежності
 |
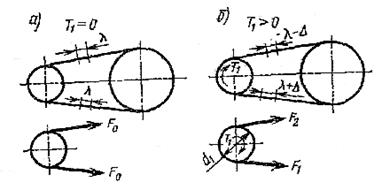На рис.1.8 показане навантаження гілок ременя у двох випадках: Т1 = 0 (рис.1.8,а) і Т1 > 0 (рис.1.8,б). Тут позначено Fo – початковий натяг ременя ; F1 і F2 –натяг ведучої та веденої гілок в навантаженій передачі; Ft = 2 T1 / d1 – окружна сила передачі.
Рис. 1.8 Сили та силові залежності
За умовою рівноваги шківа маємо:
T1 = 0,5 d1 (F1 – F2) (1.8)
або
F1 – F2 = Ft (1.9)
Зв’язок між Fo, F1 та F2 можна встановити на основі наступних роздумів.
Геометрична довжина ременя не залежить від навантаження [див. формулу (1.7)] і залишається незмінною як в ненавантаженій, так і в навантаженій передачі. З цього випливає, що додаткова витяжка ведучої гілки компенсується рівним скороченням веденої гілки (рис.1.8). Запишемо:
F1 = Fo + ∆F , F2 = Fo – ∆F (1.10)
або
F1 + F2 = 2Fo (1.11)
Із рівнянь (1.10) і (1.11) випливає:
F1 = Fo + Ft / 2 , F2 = Fo – Ft / 2 (1.12)
Отримали систему двох рівнянь з трьома невідомими Fo, F1 та F2. Ці рівняння встановлюють змінення натягу ведучої чи веденої гілок в залежності від навантаження Ft, але не дозволяють передавати це навантаження чи тягову передачу, яка зв’зана з величиною сили тертя між ременем і шківом. Така залежність встановлена Ейлером.
ПРУЖИНИ
Дата: 2019-07-24, просмотров: 193.
