Для количественной оценки результатов социологических исследований особое место занимает математико-статистический анализ. Находим среднюю арифметическую взвешенную результатов экспертного опроса на заданный вопрос: «Процесс регулирования в сфере природопользования в г. Нижнекамск и Нижнекамском районе Вы оцениваете…» по формуле 1. Для расчета средней арифметической и других показателей необходимо составить таблицу 2.7.
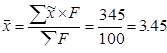 , (1)
, (1)
где ∑  – сумма средних интервалов;
– сумма средних интервалов;
F – число опрошенных.
Расчет средней арифметической взвешенной мнения опрошенных показал, что участники социологического исследования ответили в среднем на 3.45 баллов. Это говорит о том, что участники опроса ответили, что процесс регулирования в сфере природопользования в г. Нижнекамск и Нижнекамском районе не достаточно эффективен.
Поскольку средняя арифметическая взвешенная дает всего лишь среднее представление о результатах опроса в статистическом анализе часто применяются такие показатели, как средние структуры (мода, медиана), среднее квадратическое отклонение, а также коэффициент вариации.
Таблица 2.7
Сводная таблица исходных и полученных данных
Вариант 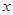
| Число опрошенных F, % | Середина интервала 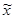
| 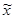 *F *F
| Накопленная частота S | 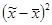
| 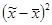 *F *F
|
| 1-2 | 5 | 1.5 | 7.5 | 5 | 398 | 19 |
| 2-3 | 10 | 2.5 | 25 | 15 | 0.9 | 9 |
| 3-4 | 75 | 3.5 | 262.5 | 90 | 0.0025 | 0.18 |
| 4-5 | 5 | 4.5 | 22.5 | 95 | 1.1 | 5.5 |
| Более 5 | 5 | 5.5 | 27.5 | 100 | 4.2 | 21 |
| Сумма | 100 | - | 345 | - | - | 54.68 |
Рассчитаем моду по формуле:
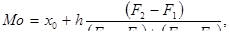 (2)
(2)
где 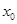 – нижняя граница модального интервала;
– нижняя граница модального интервала;
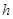 – ширина модального интервала;
– ширина модального интервала;
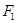 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
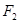 – значения частот модального интервала;
– значения частот модального интервала;
 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
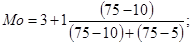
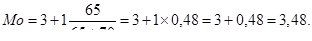
Мода как средняя структурная показывает, что наиболее встречающийся балл в ответах участников опроса является 3,48 балла. Иными словами, большинство опрошенных на данный вопрос ответили, что процесс регулирования не достаточно эффективен.
Рассчитаем медиану как среднюю структурную по формуле:
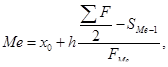 (3)
(3)
где 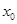 – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
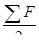 – порядковый номер медианы;
– порядковый номер медианы;
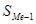 – накопленная частота до медианного интервала;
– накопленная частота до медианного интервала;
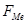 – частота медианного интервала.
– частота медианного интервала.
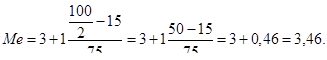
Медиана показывает, что структурный балл составляет 3,46 баллов. Это говорит о том, что 50% опрошенных ответили ниже этой оценки.
Рассчитаем среднее квадратическое отклонение по формуле:
 (4)
(4)
Расчет среднего квадратического отклонения показывает, что отклонение балла от средней арифметической составляет в среднем около 0,74 балла.
Находим коэффициент вариации по формуле:
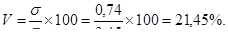 (5)
(5)
Коэффициент вариации составляет 21,45%. Это говорит о том, что уровень согласованности среди опрошенных составляет 100% – 21,45%=78,55%. И наоборот, опрошенные не согласны между собой в оценке процесса регулирования природопользованием на 21,45%. Необходимо отметить, что чем меньше значения коэффициента вариации, тем больше уровень согласованности среди опрошенных.
Находим среднюю ошибку результатов опроса под данному вопросу по формуле:
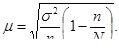 (6)
(6)
где µ – средняя ошибка выборки;
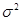 – дисперсия контролируемого признака, которая равна 0,5;
– дисперсия контролируемого признака, которая равна 0,5;
n – объем выборочной совокупности;
N – генеральная совокупность.
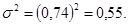
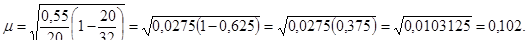
Средняя ошибка составляет 0,102 балла.
При вероятности допущения ошибкой на уровне P=0,954 находим предельную ошибку при коэффициенте доверия t=2. значения t можно найти по таблице значений интервала вероятности по справочнику.
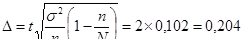 (7)
(7)
Соответственно, оценка выдаваемая опрашиваемыми с учетом предельной ошибки может быть в интервале 0,204, т.е.
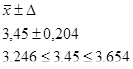
Для более наглядного представления значения статистических показателей, отражающие результаты опроса составим следующую таблицу:
| Показатель | Значения показателя |
1 
| 3,45 балла |
2 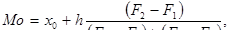
| 3,48 балла |
3 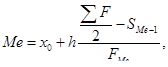
| 3,46 балла |
4 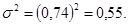
| 0,55 |
5 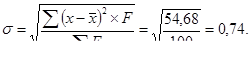
| 0,74 балла |
6 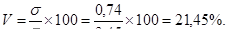
| 21,45 % |
7 
| 0,102 балла |
8 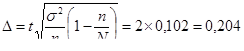
| 0,204 балла |
Дата: 2019-07-24, просмотров: 290.