Цель: Сформировать умение строить отрезки по данным формулам.

Оборудование: Циркуль, линейка.

План-коспект занятия:

1. Организационный момент.

2. Объяснение нового материала

Преподаватель: При решении задач алгебраическим методом приходится решать следующую задачу:

Даны отрезки a, b,…, l, где a, b,…, l – их длины. Выбрана единица измерения. Требуется построить отрезок х, длина которого х в этой же системе измерения выражается через длины a, b,…, l заданной формулой:

x = f (a, b,…, l)

Рассмотрим построение отрезков, заданных следующими простейшими формулами:

1) ;

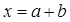2)

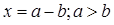
3) 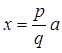, где p и q – натуральные числа;

4) 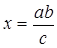 (построение отрезка – четвёртого пропорционального к данным трём).

5) ;

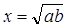6) ;

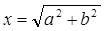7)

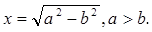
С помощью построений 1–7 можно строить отрезки, заданные более сложными формулами.

Рассмотрим пример: (решить вместе с преподавателем).

Пример 1. Пусть а, b, c и d – данные отрезки. Построить отрезок х, заданный формулой:

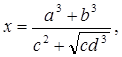
Решение: Построение отрезка выполняем в следующей последовательности:

1. Строим отрезок у, заданный формулой 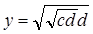(для этого дважды выполняем построение отрезка, заданного формулой 5);

2. Строим отрезок z, заданный формулой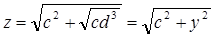

(построение отрезка, заданного формулой 6);

3. Строим отрезки u и v по формулам 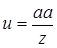 и

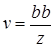
(построение отрезка по формуле 4);

4. Строим отрезок х, по формуле

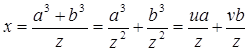
(построение отрезков, заданных формулой 4).

Построение:

Алгебраический метод решения задач состоит в следующем: Задачу формулируют так, чтобы в качестве данных фигур и искомой фигуры были отрезки. Используя подходящие теоремы, выражают длину искомого отрезка через длины данных отрезков и по найденной формуле строят искомый отрезок.

Рассмотрим пример:

Задача 1

Дан треугольник АВС. Построить три окружности с центром, соответственно в точках А, В и С так, чтобы они касались друг друга внешним образом.

Решение:

Анализ. Пусть АВС – данный треугольник, a, b, c – его стороны (AB = c, BC = a, AC = b). Задача будет решена, если мы сможем построить отрезок х по известным отрезкам a, b и c.

Видно, что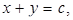

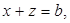
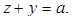
Отсюда получаем 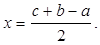 (1)

Построив отрезок х по этой формуле, проводим окружность (А, х), а затем две другие окружности (В, с – х) и (С, b – x).

Построение:

1) Строим отрезок по формуле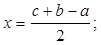

2) Строим окружность (А, х);

3) Строим окружность (В, с – х);

4) Строим окружность (С, b – х).

Доказательство: непосредственно следует из построения.

Исследование: Из формулы (1) находим:

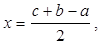
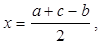
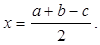 (2)

Из этих формул всегда видно, что задача всегда разрешима, так как в треугольнике АВС c + b – a > 0, a + c – b > 0, a + b – c > 0 и отрезки x, y, z могут быть построены по формулам (2).

Формулы (2) дают единственные значения радиусов искомых окружностей, поэтому задача имеет единственное решение.

5. Домашнее задание: Построить отрезок, длина которого в выбранной системе измерения равна

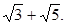
Занятие 5