Геометрическим местом точек называется совокупность точек, обладающих свойствами, исключительно им принадлежащими. Если задача приводится к определению точки, то можно отбросить одно из условий, которому эта точка должна удовлетворять; тогда искомая точка станет способна принять бесчисленное количество последовательных положений, и все эти положения составят геометрическое место точек, обладающих всеми требуемыми свойствами, кроме отброшенного. Фигура этого геометрического места чаще бывает нам заранее известна; в противном случае её надо определить вспомогательными построениями. Затем, приняв отброшенное условие и откинув какое-либо другое условие задачи, мы вновь увидим, что искомая точка станет способна принять бесчисленное множество новых положений, образующих новое геометрическое место. Определим фигуру этого нового геометрического места, если она нам неизвестна. Тогда искомая точка должна лежать и на первом и на втором геометрическом месте, а потому определяется их пересечением.
Иногда для определения точки достаточно построить одно геометрическое место, потому что другое дано в условии задачи. Если же искомая точка подчинена таким условиям, которые все в совокупности определяют только одно геометрическое место, то задача становится неопределённой.
Отсюда видно, как важно знать различные геометрические места. Знание геометрических мест иногда позволяет сразу видеть, где находится неизвестная точка.
Рассмотрим примеры.
Пример 1. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон.
Анализ. Пусть ∆АВС уже построен, тогда положение вершин В иС можно считать известным. Остаётся найти вершину А. Выясним свойства точки А. Во-первых, точка А принадлежит лучу (BA), так как дан угол АВС, во-вторых, точка А является вершиной ломанной, состоящей из двух звеньев, сумма которых равна длине данного отрезка, являющегося суммой АВ и АС сторон искомого треугольника.
На продолжении стороны ВА за точку А отложим отрезок АА1, равный отрезку АС. Теперь можно построить треугольник А1ВС по двум сторонам и углу между ними. В равнобедренном (по построению) треугольнике А1АС серединный перпендикуляр к стороне А1С пересечёт луч ВА1 в точке А.
Построение.
1) построить ∆ВА1С по сторонам ВС и ВА1 = АВ + АС и углу между ними;
2) провести серединный перпендикуляр к стороне А1С;
3) найти точку пересечения луча (BA) и построенного серединного перпендикуляра. Точка пересечения и будет искомой вершиной А.
Доказательство. В построенном ∆АВС сторона ВС, сумма сторон АВ и АС, угол В-данные.
Исследование проведём по ходу построения. Треугольник ВА1С по двум сторонам и углу между ними можно построить единственным образом. Провести серединный перпендикуляр к отрезку А1С – тоже единственным образом. Точка пересечения луча (BA) и серединного перпендикуляра существует и она единственная.
Пример 2. Постройте треугольник по стороне, разности углов при при этой стороне и сумме двух других сторон.
Анализ. Пусть ∆АВС построен, тогда положение вершин В и С можно считать известным. Остаётся найти вершину А. Во-первых, точка А принадлежит лучу (BA), так как известна разность углов В и С. Во-вторых, точка А является вершиной ломаной, состоящей из двух звеньев, сумма которых равна длине данного отрезка, являющегося суммой АВ и АС сторон искомого треугольника.
Отложим данный угол от луча ВС внутрь треугольника АВС и обозначим его через х (угол DBC обозначен через х). Тогда угол С равен Углу АВD, обозначим его через у. На продолжении стороны СА за точку А отложим отрезок АА1, равный отрезку АВ и построим треугольник СВА1. Найдём углы:
угол А1АВ равен х + 2у,
угол АВА1 = 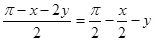 , тогда
, тогда
угол А1ВС равен 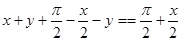 .
.
Построение.
1) построить ∆А1ВС по углу А1ВС, сторонам ВС и СА1;
2) построить серединный перпендикуляр к отрезку А1В;
3) найти точку пересечения А построенного серединного перпендикуляра со стороной А1С.
Точка пересечения и является искомой вершиной А.
Доказательство очевидно.
Алгебраический метод
Сущность метода заключается в следующем. Решение задач на построение сводится к построению некоторого отрезка (или нескольких отрезков). Величину искомого отрезка выражают через величины известных отрезков с помощью формулы. Затем строят искомый отрезок по полученной формуле.
Пример 1. Провести окружность через две точки А и В так, чтобы длина касательной к ней, проведённой из точки С равнялась а.
Анализ. Пусть через точки А иВ проведена окружность так, что касательная к ней из точки С равняется а. Так как через три точки можно провести окружность, то проведём СВ и определим положение точки К. Полагаем СК = х и СВ = с; тогда по свойству касательной сх = а2.
Построение.
1) для построения х чертим полуокружность на ВС и дугу (С, а);
2) опустим LK ^ BC;
3) с × КС = а2; поэтому х = КС, и точка К будет искомая;
4) восстановив перпендикуляры из середин АВ и КВ до их пересечения найдём искомый центр О;
5) чертим окружность (О, ОА);
МС – искомая касательная.
Доказательство. МС2 = СВ×КС = 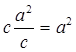 и МС = а, как и требовалось.
и МС = а, как и требовалось.
Исследование. Выражение a £ с – условие существования решения нашей задачи, так как только при этом условии дуга (С, а) пересечёт окружность СLB.
Пример 2. Из вершин данного треугольника как из центров опишите три окружности, касающиеся попарно внешним образом.
Анализ. Пусть АВС – данный треугольник, а, b , c – его стороны, х, у, z – радиусы искомых окружностей. Тогда 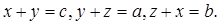 Поэтому
Поэтому 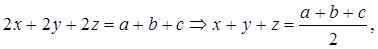 откуда
откуда 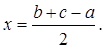
Построение.
1) проводим окружность S1(A, x);
2) S2(B, c – x);
3) S3(C, b – x).
Доказательство. Найдём сумму радиусов окружностей S1 и S3:
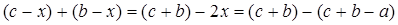 = ВС.
= ВС.
Получили, что сумма радиусов равна расстоянию между их центрами, что и доказывает касание окружностей S2 и S3.
Исследование. Задача всегда однозначно разрешима, поскольку:
1. в треугольнике АВС сумма сторон 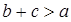 , и поэтому отрезок х может быть построен;
, и поэтому отрезок х может быть построен;
2. 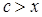 , потому что
, потому что 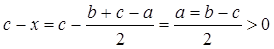 (так как
(так как 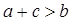 );
);
3. 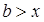 , так как
, так как 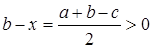 .
.
Метод инверсии
Пусть нам дана некоторая кривая М и неподвижная точка К – начало или центр инверсии. Возьмём на кривой М точку А и на прямой КА определим точку А1 так, чтобы абсолютное значение КА·КА1 = к2, где к – есть постоянная длина, то при движении точки А по кривой М точка А1 опишет новую кривую N, которая называется обратной или инвертированной кривой.
Пусть у нас имеется фигура, состоящая из прямых и окружностей. Если эту фигуру инвертировать, то прямые и окружности превратятся в известные прямые и окружности, или в одни окружности, которые будут пересекаться под теми же углами, как и в данной фигуре. Если какая-нибудь точка данной фигуры представляла, например, вершину какого-нибудь угла, то в обратной фигуре она представит, вообще, точку пересечения окружностей, пересекающихся под тем же углом. Словом, обратная фигура удерживает до мельчайших подробностей своеобразное сходство с данной фигурой.
Зная отображённую фигуру и положение начала инверсии, нередко можно легко отгадать форму основной фигуры; что касается её размера, то для этого нужно знать степень инверсии.
Пример 1. Даны точка К две прямые АВ и ВС. Провести секущую КХY так, чтобы KX·KY = k 2(k – есть данная длина).
Анализ. Искомая точка Y есть пересечение прямой ВА с прямой, инвертированной к ВС с центром инверсии К и степенью к2.
Построение.
1) опустим KL ^ BC;
2) на ВС отложим LN = k;
3) проведём MN ^ KN до пересечения KL в точке М;
4) окружность, описанная на диаметре МК встретит АВ в искомой точке.
Пример 2. Даны точки А, В и С. Через В провести прямую так, чтобы расстояния АХ и CY от этой прямой удовлетворяли равенству
АХ2 - СY2 = к2.
Решение. Из равенства (АХ + CY) (AX – CY) = k 2 вытекает необходимость ввести в чертёж сумму и разность AX и CY. Поэтому переносим параллельно CY в С1Х и AC1·AY1 = k 2. Если взять за центр инверсии А и за коэффициент к2, то С1 – есть точка окружности, инвертированной к прямой DY1; диаметр этой окружности равен АС1. Так как точки D и J соответственные, то AD·AJ = k 2, что даёт возможность построить точку J. Тогда для определения точки С1 имеем JC1 ^ AD и окружность, диаметр которой равен АС.
Эксперимент
Практические занятия по теме «Методы решения задач на построение».
Цели: 1. Формирование знаний об этапах решения задач на построение и умений их осуществлять;
2. Формирование представлений об основных методах решения задач на построение;
3. Формирование навыков самостоятельной работы.
План занятий:
| Этапы изучения темы | Тема занятия | Количество часов |
| 1. Пропедевтический этап | Основы конструкти- вной геометрии. Ос- новные геометричес- кие построения. | 2 |
| 2. Систематический этап | 1. Метод пересечения фигур 2. Алгебрaический метод 3. Метод параллель ного переноса 4. Метод подобия | 5 |
| 3. Итоговый этап | Самостоятельная ра- бота | 1 |
Дата: 2019-07-24, просмотров: 321.