Вопрос о выборе той или иной схемы решения конструктивной задачи является чисто методическим вопросом.

Решение геометрической задачи является вполне доброкачественным, если оно проведено, например, последующей схеме:

1. Устанавливается конечное число случаев, исчерпывающих все возможности в выборе данных.

2. Для каждого случая дается ответ на вопрос, имеет ли задача решение и сколько.

3. Для каждого случая, когда задача имеет решение, дается способ нахождения (с помощью данных геометрических инструментов) каждого из возможных решений или устанавливается, что оно не может быть получено данными средствами.

Этой схемы придерживаются в научных статьях и монографиях; однако она мало пригодна для учебных целей, особенно в условиях средней школы.

При решении каждой сколько-нибудь сложной задачи на построение возникает вопрос о том, как нужно рассуждать, чтобы разыскать способ решения задачи, чтобы получить все решения задачи, чтобы выяснить условия возможности решения задачи и т.п. Поэтому при решении конструктивных задач в учебных условиях рекомендуется пользоваться известной схемой решения, состоящей из следующих четырех этапов: 1) анализ; 2) построение; 3) доказательство; 4) исследование.

Конечно, эта схема не является безусловно необходимой и неизменной, не всегда удобно и целесообразно строго разделять отдельные ее этапы и в точности осуществлять их в указанном порядке. Но по большей части указанная схема серьезно помогает при решении конструктивных задач. Рассмотрим каждый этап этой схемы.

1. Анализ. Это подготовительный и в то же время наиболее важный этап решения задачи на построение, так как именно он дает ключ к решению задачи. Цель анализа состоит в установлении таких зависимостей между элементами искомой фигуры и элементами данных фигур, которые позволили бы построить искомую фигуру. Это достигается с помощью построения чертежа-наброска, изображающего данные и искомые примерно в том расположении, как это требуется условием задачи. Этот чертеж можно выполнять «от руки». Иногда построение чертежа сопровождают словами: «предположим, что задача уже решена».

На вспомогательном чертеже следует выделить данные элементы и важнейшие искомые элементы. Практически часто удобнее начинать построение вспомогательного чертежа не с данной фигуры, а с примерного изображения искомой фигуры, пристраивая к ней данные так, чтобы они находились в отношениях, указанных в условии задачи. Например, если нужно построить треугольник по биссектрисе, медиане и высоте, проведенным из одной вершины, то при анализе удобнее сначала изобразить произвольный треугольник, а затем уже проводить в нем указанные в задаче линии.

Если вспомогательный чертеж не подсказывает непосредственного способа построения искомой фигуры, то пытаются обнаружить какую-либо часть искомой фигуры или вообще некоторую фигуру, которая может быть построена и которой затем можно воспользоваться для построения искомой фигуры. В более общем случае рассуждение ведется следующим образом. Подмечают, что построение искомой фигуры Ф сводится к построению некоторой другой фигуры Ф 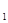. Затем подмечают, что построение фигуры Ф  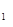сводится к построению фигуры Ф  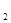и т.д. После конечного числа шагов можно прийти к некоторой фигуре Ф 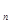, построение которой уже известно.

Пусть, например, требуется построить треугольник по основанию и по медиане и высоте, проведенным к этому основанию. Рассматривая вспомогательный чертеж (рис. 5), замечаем, что треугольник АВС можно легко построить, если будет построен треугольник ВDE: тогда останется только отложить по обе стороны от точки Е на прямой DE отрезки, равные половине данного основания. Но треугольник ВDE прямоугольный и строится по гипотенузе m и катету h.

Полезно учесть следующие частные замечания, помогающие при проведении анализа.

1) Если на вспомогательном чертеже не удается непосредственно заметить необходимые для решения связи между данными и искомыми элементами, то целесообразно ввести в чертеж вспомогательные фигуры: соединить уже имеющиеся точки прямыми, отметить точки пересечения имеющихся линий, продолжить некоторые отрезки и т.д. Иногда бывает полезно проводить параллели или перпендикуляры к уже имеющимся прямым.

Пусть, например, требуется построить прямую, проходящую через данную точку А и равноудаленную от двух данных точек В и С. Построение чертежа – наброска удобно начать с искомой фигуры: строим сначала прямую а (рис. 6), на ней выбираем точку А и на равных расстояниях от прямой а выбираем (по разные стороны от прямой) точки В и С.

После этого еще не возникают на чертеже такие связи, которые позволили бы решить задачу. Проведем к прямой а перпендикуляры ВВ  и СС , построим отрезок ВС и отметим точку М пересечения отрезка ВС с прямой а. Легко заметить, что М – середина отрезка ВС, а отсюда уже ясен способ построения.

2) Если по условию задачи дана сумма или разность отрезков или углов, то эти величины следует изобразить на вспомогательном чертеже, если их еще нет на нем.

3) В процессе проведения анализа бывает полезно вспомнить теоремы и раннее решенные задачи, в которых встречаются зависимости между элементами, сходные с теми, о которых говориться в условии рассматриваемой задачи.

4) Проводя анализ на основании изучения некоторого чертежа – наброска, мы невольно связываем свои рассуждения в известной мере с этим чертежом. Так, в примере, иллюстрирующем пункт 1), мы избрали точки В и С по разные стороны от прямой а, а в то время как можно было избрать их и по одну сторону от этой прямой. Тот способ решения, к которому мы приходим на основании анализа, может поэтому оказаться пригодным лишь для некоторых частных случаев. Чтобы получаемый нами способ решения был пригоден для возможно более широкого выбора данных, желательно изображать искомую фигуру в возможно более общем виде. Например, искомый треугольник, если в условии задачи нет специального указания о его форме, надо изображать как разносторонний, четырехугольник – как неправильный и т.п. Чем более общий случай мы разберем при анализе, тем проще будет провести в дальнейшем полное решение задачи.

Рассмотрим еще один пример анализа. Требуется вписать окружность в данный треугольник. Пусть АВС – данный треугольник (рис. 7). Чтобы вписать в него окружность, надо определить положение ее центра и найти величину радиуса.

Представим себе, что точка О – центр вписанной окружности, а ОМ – радиус проведенный в какую-либо из точек касания окружности к сторонам треугольника (например, в точку касания окружности к стороне АВ). Тогда отрезок ОМ перпендикулярен к прямой АВ. Поэтому ОМ – расстояние центра вписанной окружности от стороны треугольника АВ. Так как все радиусы окружности равны, то центр окружности одинаково удален от всех сторон треугольника и, следовательно, прямые ОА, ОВ и ОС служат биссектрисами (внутренних) углов треугольника АВС. Этих соображений, очевидно, достаточно для построения центра и определения радиуса искомой окружности.

2. Построение. Данный этап решения состоит в том, чтобы указать последовательность основных построений (или раннее решенных задач), которые достаточно произвести, чтобы искомая фигура была построена.

Построение обычно сопровождается графическим оформлением каждого его шага с помощью инструментов, принятых для построения.

В качестве примера обратимся опять к задаче о построении окружности, вписанной в данный треугольник АВС. Как показывает проведенный выше анализ этой задачи, для построения искомой окружности нужно последовательно построить (см. рис. 7):

1) биссектрисы каких-либо двух внутренних углов данного треугольника;

2) точку их пересечения О;

3) прямую, проходящую через точку О, перпендикулярно прямой АВ;

4) основание М проведенного перпендикуляра;

5) окружность (О, ОМ).

3. Доказательство. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет всем поставленным в задаче условиям.

Так, чтобы провести доказательство правильности приведенного выше построения окружности, вписанной в данный треугольник, надо установить, что построенная нами окружность (О, ОМ) действительно коснётся всех сторон треугольника АВС. Для этого, прежде всего заметим, что прямая АВ касается проведённой окружности, так как эта прямая перпендикулярна к радиусу ОМ.

Вместе с этим ясно, что радиус окружности равен расстоянию её центра от стороны АВ данного треугольника АВС. Далее замечаем, что центр окружности О одинаково удалён от всех сторон треугольника, так как лежит на пересечении биссектрис углов треугольника. Следовательно, расстояние центра окружности от стороны АС или от стороны ВС также равно радиусу построенной окружности, так что если провести через О перпендикуляры к сторонам треугольника АС и ВС, то основания этих перпендикуляров (точки N и Р на рис. 8) расположатся на той же окружности.

Таким образом, каждая из прямых АС и ВС перпендикулярна к соответствующему радиусу в конце его, лежащем на окружности, и поэтому каждая из этих прямых касается построенной окружности.

Доказательство обычно проводится в предположении, что каждый шаг построения действительно может быть выполнен.

4. Исследование. При построении обычно ограничиваются отысканием одного какого-либо решения, причем предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно ещё выяснить следующие вопросы:

1) всегда ли (т.е. при любом ли выборе данных) можно выполнить построение избранным способом;

2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить;

3) сколько решений имеет задача при каждом возможном выборе данных.

Рассмотрение всех этих вопросов и составляет исследование. Таким образом, исследование имеет целью установить условия разрешимости и определить число решений.

Иногда ставится также задача: выяснить при каких условиях искомая фигура будет удовлетворять тем или иным дополнительным требованиям. Например, может быть поставлен вопрос: при каких условиях искомый треугольник будет прямоугольным или равнобедренным? Или такой вопрос: при каких условиях искомый четырёхугольник окажется параллелограммом или ромбом?

Нередко школьники проводят исследование, в известной мере произвольно выбирая те или иные случаи, причём неясно, почему рассматриваются именно такие, а не какие-либо иные случаи. Остаётся неясным также, все ли возможные случаи рассмотрены. При исследовании решения какой-либо сложной задачи такой подход может привести к потере решений, к тому, что некоторые случаи не будут рассмотрены.

Чтобы достигнуть необходимой планомерности и полноты исследования, рекомендуется проводить исследование «по ходу построения». Сущность этого приёма состоит в том, чтобы перебрать последовательно все шаги, из которых слагается построение, и относительно каждого шага установить, всегда ли указанное на этом шаге построение выполнимо, а если выполнимо, то сколькими способами.

Для этого необходимо:

1) Выяснить, всегда ли существуют в действительности точки, прямые, окружности или другие фигуры, построение которых предполагается осуществить на каждом шаге намеченного построения, или же их существование зависит от специального выбора положения или размеров тех или иных фигур. Например, если предполагается построить точки пересечения окружности с прямой, то надо заметить, что существование таких точек зависит от соотношения между радиусом этой окружности и расстоянием центра окружности от прямой.

Дальнейшее исследование надо проводить только для тех случаев, когда построение возможно, т.е. когда каждый шаг действительно приводит к построению искомых фигур.

2) Для каждого случая, когда решение существует, определить, сколько именно точек, прямых, окружностей и т.д. даёт каждый шаг построения. Например, если строятся точки пересечения окружности и прямой, то надо учесть, что таких точек будет две, если радиус окружности больше расстояния от центра до прямой, и одна, если радиус окружности равен расстоянию центра от прямой.

3) Учитывая результаты исследования каждого шага, обратиться к задаче в целом и установить, при каких условиях расположения денных фигур или при каких соотношениях их размеров задача действительно имеет решение, а при каких его не существует. Если возможно, выразить условия разрешимости формулой (в форме неравенств или равенств).

4) Определить число возможных решений при каждом определённом предположении относительно данных, при котором эти решения существуют.

В итоге таких рассуждений решается вопрос о возможности построения данным способом. Но остаётся ещё открытым вопрос: не возникнут ли новые решения, если изменить как-либо способ построения? Иногда удастся доказать, что всякое решение данной задачи совпадает с одним из уже полученных решений; в этом случае исследование можно считать законченным. Если же это не удаётся, то можно предположить, что задача имеет другие решения, которые могут быть найдены другими способами. В этих случаях полезно ещё раз обратиться к анализу и проверить, нет ли каких-либо иных возможных случаев расположения данных или искомых фигур, которые не были предусмотрены ранее проведённым анализом.