У дослідженні кредиту найбільш важливим питанням є вміння визначити величину позикових процентів. Традиційно їхню величину визначають за формулою:
К% = КП Е% ТП,(3.1)
де К% – загальна вартість нарахованих процентів;
Кп – сума наданої позики;
Е% – банківський процент за певний час;
Тп - тривалість позики.
Коли до формули (3.1) застосувати категорійний апарат аналітичної економетрії, отримаємо:
К% = МП Е%, (3.2)
де М = Кп • Тп – момент позикової вартості.
Формула (3.2) є найбільш загальною формулою, якою ми будемо користуватися для розрахунку величини нарахованих процентів.
Точніший результат можна отримати, використовуючи формулу:
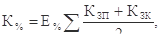(3.3)
де Кзп, Кзк — величина заборгованості на початок і кінець розглянутого планового періоду.
В окремих дослідженнях, коли розраховують вартість довготермінового кредиту, основну увагу звертають не моменти вартості, що утворюються внаслідок зміни величини заборгованості, а на значення цих заборгованостей. З огляду на це для дискретного випадку надання або повернення позики пропонується користуватися такою формулою:
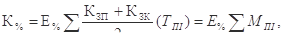(3.4)
де Тпі — тривалість і-го планового періоду, протягом якого користуються позикою;
Мпі — момент позикової вартості для цього періоду.
Використовуючи формулу моментів позикової вартості, отримаємо аналітичний вираз для визначення величини нарахованих процентів за методикою простих процентів, якщо кредит погашається рівномірно
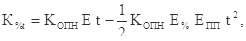(3.5)
де Копн – загальна величина наданої позики;
t – період повернення позики;
Епп – оборотність повернення позики.
Останнім часом для розрахунку довготермінового кредиту застосовують методику ануїтету, поєднуючи з дисконтуванням вартості, тобто застосовують методику нарахування складних процентів:
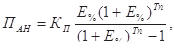(3.6)
де Пан — значення ануїтету (величина періодичних виплат для повернення позики); інші попередні показники.
Для обґрунтування викладеного розглянемо такий приклад. Припустимо, що АКБ “ТАС-Комерцбанк” надав кредит па суму 100 тис. грн. під 30% річних. Клієнт банку зобов'язався повернути кредит протягом 3,5 років. Проаналізуємо три методи повернення кредиту: за дискретними виплатами, безперервними виплатами та за методикою ануїтету.
Метод 1. Клієнт повертає банку кредит дискретними виплатами. Повернення боргу відбувається шляхом таких виплат (тис. грн.): перший рік – 40, другий – 30, третій – 20 і четвертий – 10. Розрахунок кредиту виконано за формулою (3.4), результати зведено в табл. 3.1.
Таблиця 3.1
Розрахунок повернення кредиту за дискретним методом
| Роки | 1 | 2 | 3 | 4 |
| Заборгованість на початок року | 100 | 60 | 30 | 10 |
| Нараховані проценти за рік | 24 | 13,5 | 6 | 0,75 |
| Сумарні нараховані проценти | 24 | 37,5 | 43,5 | 44,25 |
Основні залежності показано на рис. 3.1, де К%т – загальна величина нарахованих процентів; Кбо – початкова величина боргу (позики); М% і Мб – моменти вартості від нарахованих процентів і повернутого боргу.
|
|
|
|
|
|
|
|
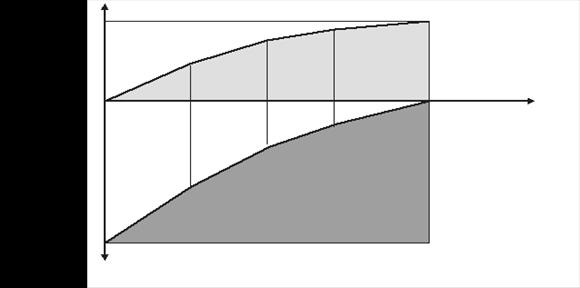
Рис. 3.1. Графічне зображення основних показників кредиту, розрахованого для дискретного методу повернення боргу
Метод 2. Клієнт повертає банку кредит безперервними виплатами (щотижня). Погашення боргу відбувасться рівномірно. У цьому разі розрахунок проводиться за формулою (3.5). Результати розрахунку зведено в табл. 3.2, а основні залежності показано на рис. 3.2.
Таблиця 3.2
Розрахунок повернення кредиту за рівномірним погашенням методом
| Роки | 1 | 2 | 3 | 4 |
| Заборгованість на початок року | 100 | 71,43 | 42,86 | 14,28 |
| Нараховані проценти за рік | 25,71 | 17,14 | 8,58 | 1,07 |
| Сумарні нараховані проценти | 25,71 | 42,85 | 51,43 | 52,5 |
|
|
|
|
|
|
|
|
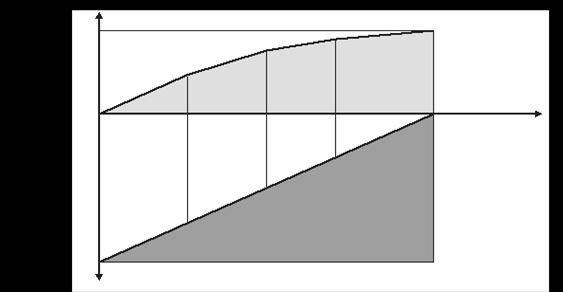
Метод 3. Повернення кредиту за методикою ануїтету – формула (3.6). Недоліком цієї методики є те, що в цьому разі також потрібно розраховувати кратну кількість планових періодів. Оскільки тривалість позики становить 3,5 роки, то прийнявши, що сплата буде використовуватися через півроку, таких періодів буде 7. Окрім того, щоб дотримувалося правило розмірностей, необхідно перейти до піврічної величини банківського процента. Тобто вона дорівнюватиме Е% = 15 % . Тоді величина ануїтету становитиме:
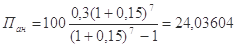тис. грн.
Результати розрахунку зведено в табл. 3.3, а основні залежності показано на рис. 3.3, де Пан – величина ануїтету..
Таблиця 3.3
Розрахунок повернення позики за методом ануїтету, тис. грн.
| Півріччя | Залишок позики на початок року | 15% піврічних | Залишок загальної суми заборгованості на кінець року | Річна плата (ануїтет) | Річна плата тільки за позику |
| 1 | 100 | 15 | 115 | 24,036 | 9,036 |
| 2 | 90,964 | 13,644 | 104,609 | 24,036 | 10,391 |
| 3 | 80,572 | 12,086 | 92,658 | 24,036 | 11,95 |
| 4 | 68,622 | 10,293 | 78,916 | 24,036 | 13,743 |
| 5 | 54,88 | 8,232 | 63,112 | 24,036 | 15,804 |
| 6 | 39,076 | 5,861 | 44,937 | 24,036 | 18,175 |
| 7 | 20,901 | 3,135 | 24,036 | 24,036 | 20,901 |
| Усього | - | 68,252 | - | 168,252 | 100 |
Коли виконують порівняння різних варіантів розрахунку кредиту, основну увагу приділяють сумі нарахованих процентів.
|
|
|
|
|
|
|
|
|
|
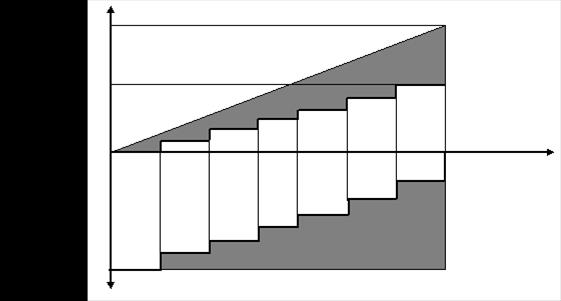
Рис. 3.3 Графічне зображення основних показників кредиту, розрахованого для третього методу повернення боргу (за методикою ануїтету)
У нашому прикладі сума нарахованих процентів становитиме (тис. грн.): 44,25; 52,5 і 68,252 – відповідно для кожного методу повернення боргу. Порівнюючи ці значення, можна нібито прийти до висновку, що найбільшу суму грошей банк отримає, коли кредит буде надавати за третьою методикою, а найменшу – за першою. Проте такий поверхневий аналіз не завжди підтверджується більш ретельним і обґрунтованим, оскільки в дослідженні будь-якої форми вартості основна увага має приділятися тому, як грошові або вартісні потоки розміщуються в просторі і часі, тобто необхідно досліджувати моменти вартості.
Для дослідження таких складних процесів ми рекомендуємо застосовувати запропонований нами економетричний показник – масу вартості В, яка визначається за формулою
В = МП / ТП(3.7)
Найвигіднішим для банку буде той варіант, котрий принесе йому найбільшу масу вартості.
Момент позикової вартості Мп складається з двох елементів: з повернутого боргу Мб і нарахованих процентів М%. Розрахунки для трьох розглянутих випадків наведені у табл. 3.4.
Таблиця 3.4
Порівняння трьох методів розрахунку процентів
| Метод розрахунку | Моменти вартості, тис. грн. • рік | Кінцеві результати розрахунку, тис. грн. | |||
| Мб | М% | Мп | за масою вартості | за нарахованими процентами | |
| 1 | 202,5 | 105,1875 | 307,6875 | 87,91 | 44,25 |
| 2 | 175 | 122,5 | 297,5 | 85 | 52,5 |
| 3 | - | - | 294,441 | 84,126 | 68,252 |
З таблиці видно, що за масою вартості найкращим є дискретний метод нарахування відсотків, а за обсягом нарахованих відсотків – останній метод ануїтету. Вибір найкращого і найгіршого варіантів повернення боргу залежить, головним чином, від прийнятого для порівняння показника (критерію оптимальності) – від маси вартості чи нарахованих процентів. За цими критеріями розглянуті варіанти позики мають зовсім протилежні результати. Проте маса вартості показує зростання загального капіталу банку, а нараховані проценти лише окремої їхньої частини, до того ж без врахування, як вони змінюються в часі. Тому, на нашу думку, для АКБ “ТАС-Комерцбанк” для дослідження позикової вартості правильніше використовувати методику за показником маса вартості, яким можна визначати середню масу капіталу, що функціонує в банку (або який утворюється в банку) протягом розглянутого проміжку часу. В нашому випадку найкращим виявився метод нарахування відсотків за дискретною методикою.
Дата: 2019-07-24, просмотров: 251.
