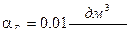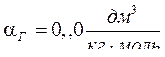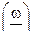Итак , имеем 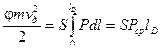 или
или 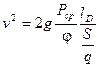 (9.30)
(9.30)
Из полученного выражения (9.30) следует ,чтобы увеличить скорость снаряда необходимо :
1. увеличить среднее давление пороховых газов -Рср
2. увеличить длину ствола- lD
3. уменьшить поперечную нагрузку снаряда - 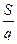
4. уменьшить 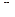 .
.
Наличие пути снаряда –lD увеличивает использование энергии газов (  ) и поэтому являются одним из возможных методов повышения скорости снаряда , однако этот способ по двум причинам ограничен ,во-первых с увеличением lD убывает Рсри с некоторой величины lD дальнейшее увеличение будет мало влиять на произведение РсрlD ,а во-вторых ,орудийный ствол должен быть такой длины ,чтобы он не прогибался под собственным весом и удовлетворял другим техническим требованиям.
) и поэтому являются одним из возможных методов повышения скорости снаряда , однако этот способ по двум причинам ограничен ,во-первых с увеличением lD убывает Рсри с некоторой величины lD дальнейшее увеличение будет мало влиять на произведение РсрlD ,а во-вторых ,орудийный ствол должен быть такой длины ,чтобы он не прогибался под собственным весом и удовлетворял другим техническим требованиям.
Увеличение среднего давления при заданном наибольшем давлении- Рm и заданном Wкн ,можно добиться разными путями .
1. применением прогрессивных форм пороха
2. применением флегматизированных порохов
3. применением цилиндро-конических каналов
4. применением камор с большим уширением
5. многокамерных орудий
6. увеличение относительного веса заряда
На рис. …… показаны различные кривые р(t) при одинаковых максимальных давлениях .
Кривая 1-соответствует мгновенному сгоранию пороха .
Кривая 2- соответствует горению прогрессивного пороха
Кривая 3-соответствует дегрессивного пороха
Кривая 4-соответствует горению "толстого" пороха.
Из этих кривых –кривая 2 имеет наибольшее значение среднего давления .
При заданном наибольшем давлении с возрастанием прогрессивности возрастает также плотность заряжания , достигая 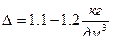 . В то время как для дегрессивных порохов
. В то время как для дегрессивных порохов 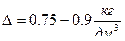 .
.
Плотность заряжания.
Влияние на величину скорости незначительно, флегматизация способствует дополнительному увеличению прогрессивности ,т.е. будет увеличивать среднее давление .
Применение конического ствола увеличивает среднее значение –Рср ,что видно из расчетов проверенных И.П.Граве для винтовки .
Результаты представлены в таблице:
Таблица 19
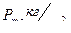
| 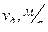
| R | 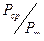
| 
| канал |
| 2380 | 834 | 0,441 | 0,489 | 0,235 | цилиндрический |
| 2375 | 860 | 0,376 | 0,522 | 0,303 | цилиндро-конический |
В числе средств , способствующих увеличению дульной скорости , определенное место занимает камора со значительным уширением . При малых относительных зарядах , уширение каморы почти не влияет на баллистику орудия ,но роль уширения возрастает с возрастанием относительного веса заряда 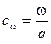 . Камора с уширением позволяет значительно значительно уменьшить перепад давления отдна канала к дну снаряда , а следовательно повысить среднее давление .
. Камора с уширением позволяет значительно значительно уменьшить перепад давления отдна канала к дну снаряда , а следовательно повысить среднее давление .
Переходя к оценке влияния поперечной нагрузки снаряда , отметим ,что это связано с конструкцией снаряда (применением подкалиберных снарядов) . Уменьшению поперечной нагрузки способствует и применение цилиндроконических стволов из формулы (9.23)дульная скорость увеличивается с увеличением мощности пороха (его потенциала 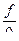 ) и относительного веса заряда
) и относительного веса заряда 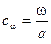 ,т.к. с возрастанием
,т.к. с возрастанием  увеличивается и коэффициент фиктивности
увеличивается и коэффициент фиктивности 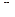 ,то скорость возрастает медленее , чем
,то скорость возрастает медленее , чем  ,однако возможность значительного увеличения
,однако возможность значительного увеличения  выдвигает этот способ повышения скорости на первое место ( подробнее об этом будет позднее ).
выдвигает этот способ повышения скорости на первое место ( подробнее об этом будет позднее ).
С возрастанием мощности пороха скорость также будет возрастать , но этот метод ограничен в своих возможностях ,т.к. с увеличением мощности пороха резко падает живучесть ствола . И наконец , из формулы (9.28) следует ,что для орудий наибольшей мощности (т.е. такое орудие ,в котором будет осуществляться наибольшая плотность энергии ) с возрастанием
наибольшего давления будет возрастать и дульная скорость снаряда обычно R изменяется в пределах 0,4-0,6
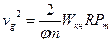 (9.31)
(9.31)
И, наконец , уменьшение коэффициента фиктивности - 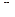 приводит к увеличению скорости снаряда . Насколько это возможно –рассмотрим подробнее.
приводит к увеличению скорости снаряда . Насколько это возможно –рассмотрим подробнее.
9.4 Коэффициент учета второстепенных работ – коэффициент фиктивности - 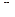 .Учет теплоотдачи и прорыва пороховых газов .
.Учет теплоотдачи и прорыва пороховых газов .
Рассмотрим виды работ совершаемые пороховыми газами :
1. L1 - работа поступательного движение снаряда – главная работа .
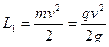 (9.32)
(9.32)
2. L2- работа, затрачиваемая на вращение снаряда 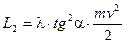 (9.33) ,
(9.33) ,
где 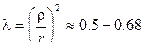
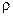 -радиус инерции снаряда , определяемый по формуле
-радиус инерции снаряда , определяемый по формуле 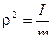 , где I- момент инерции относительно оси вращения
, где I- момент инерции относительно оси вращения
r=d/2- радиус сечения снаряда
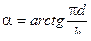 -угол нарезки
-угол нарезки
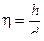 - крутизна нарезов
- крутизна нарезов
h- шаг нарезки
обычно 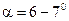
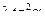 от 0,25% до 2,5%
от 0,25% до 2,5%
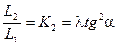 К2=0,0025-0,025
К2=0,0025-0,025
L3- работа на преодоление трения между пояском снаряда и внутренней поверхности канала ствола , а также на преодоление трением между центрующими утолщениями снаряда и полями нарезов 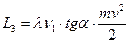 (9.34) ,где
(9.34) ,где 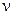 1 -коэффициент трения
1 -коэффициент трения
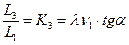
4. L4- работа затрачиваемая на перемещение газов самого заряда и несгоревшего пороха . В предположении о постоянстве плотности 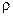 газопороховой смеси по всему за снарядному пространству .т.е. плотность
газопороховой смеси по всему за снарядному пространству .т.е. плотность 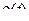 зависит только от времени и не зависит от координаты сечения и в самом сечении , энергия , затрачиваемая на перемещение заряда , будет выражаться зависимостью :
зависит только от времени и не зависит от координаты сечения и в самом сечении , энергия , затрачиваемая на перемещение заряда , будет выражаться зависимостью : 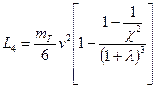
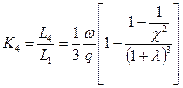 (9.35) , где
(9.35) , где 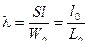 ,
, 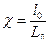 , где l0- приведенная длина каморы =
, где l0- приведенная длина каморы = 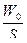
L0- действительная длина каморы
l- путь пройденный снарядом
Работа L4 вычисленная по формуле (9.35) будет больше действительной работы , т.к. плотность газопороховой смеси уменьшается в направлении к снаряду , что доказывают газодинамические расчеты .
5. Работа затрачиваемая на перемещение откатных частей.
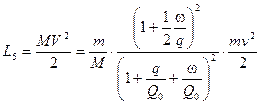 (9.36)
(9.36)
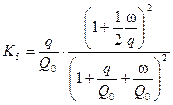 , где
, где 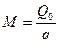 -масса откатных частей ; Q0 –вес откатных частей .
-масса откатных частей ; Q0 –вес откатных частей .
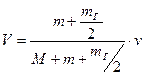 (9.37) ,где V –скорость откатных частей
(9.37) ,где V –скорость откатных частей
mг= 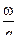 -масса заряда, т.к.
-масса заряда, т.к. 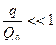 и
и 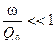 , то
, то 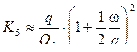
L6 –работа , расходуемая на врезание ведущего пояска в нарезы . Как правило не учитывается и может быть учтено косвенно в момент вылета снаряда из ствола .
L7 –работа, расходуемая на преодоление снарядом сопротивления воздуха , находящегося в канале орудия . Этой работой при малых скоростях пренебрегают . Однако при скоростях 2,5-3 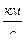 противодавление уже составляет 150-300
противодавление уже составляет 150-300 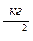 и учет противодавления необходим .
и учет противодавления необходим .
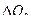 - тепловая энергия , расходуемая во время выстрела на нагрев стенок ствола , гильзы и снаряда – потеря на теплоотдачу . Учитывается путем уменьшения силы пороха ,-f.
- тепловая энергия , расходуемая во время выстрела на нагрев стенок ствола , гильзы и снаряда – потеря на теплоотдачу . Учитывается путем уменьшения силы пороха ,-f.
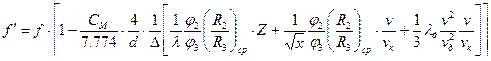 (9.38)
(9.38)
в момент времени t при t=0 , 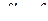
при t=tд
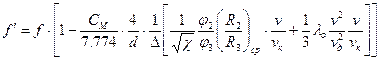 ,где
,где
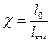 ;
; 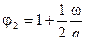 ;
; 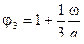 ;
; 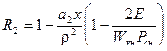 ;
; 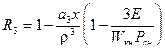 ;
;
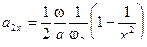 ;
; 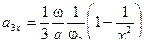 ;
; 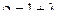 ;
; 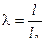 ;
; 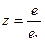 ;
; 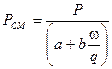 ;
;
l –путь снаряда
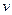 -скорость снаряда
-скорость снаряда
См% -определяется по кривой С% от tк при  кг/дм2
кг/дм2
d –калибр снаряда
lкм –длина каморы
Wкн –объём канала ,включая камору
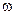 - вес заряда
- вес заряда
 q –вес снаряда
q –вес снаряда
Рсн – давление на снаряд
Таким образом , сила пороха по мере движения снаряда по каналу за счет теплоотдачи убывает ; она зависит от :
1) калибра-d
2) плотности заряжания - 
3) коэффициента уширения каморы - 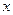
4) относительного пути снаряда - 
5) отношения скоростей
При выводе использовалось предположение , сделанное Мюреуром :
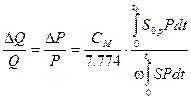 и соотношение
и соотношение 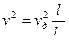 , сделанное профессором Вентцелем.
, сделанное профессором Вентцелем.
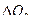 - энергия , теряемая газами , прорывающимися по зазорам между пояском снаряда и стенками канала орудия.
- энергия , теряемая газами , прорывающимися по зазорам между пояском снаряда и стенками канала орудия.
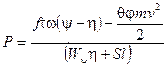 (9.39)
(9.39)
где 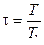 ;
; 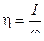 - относительная часть прорвавшихся газов
- относительная часть прорвавшихся газов
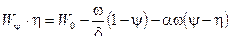
Если расход газа невелик , то 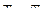 , или с учетом теплоотдачи
, или с учетом теплоотдачи  .
.
Значение 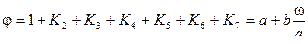 ,где a=1.09-1.03 и b=
,где a=1.09-1.03 и b= 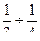 - для цилиндрических каналов и
- для цилиндрических каналов и 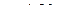 и
и 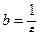 - для конических каналов.
- для конических каналов.
9.5 Анализ изменения давления пороховых газов в канале ствола от условий заряжания .
Имея формулу для давления из основного уравнения пиродинамики (9.19)
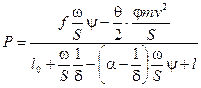 ,
,
исследуем ,как будет меняться давление в зависимости от пути и времени . Для этого найдем производные :
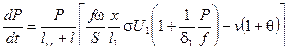 (9.40)
(9.40)
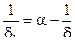 ,
, 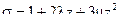 или
или 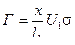 ,
, 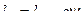 ,
, 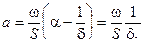 ,
,
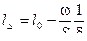
Как видно из выражения (9.40) нарастание давления зависит от многих факторов .
В момент формообразования Р=Р0
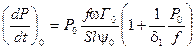 , нарастание давления зависит от Р0,f и
, нарастание давления зависит от Р0,f и 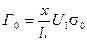 ,и обратно пропорционально
,и обратно пропорционально 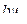 , при Р0=0 (для миномета ) ,тангенс угла наклона будет равен 0 . И далее тангенс угла наклона возрастает до точки перегиба и далее тангенс угла наклона убывает до 0 и далее становится отрицательным за счет значения
, при Р0=0 (для миномета ) ,тангенс угла наклона будет равен 0 . И далее тангенс угла наклона возрастает до точки перегиба и далее тангенс угла наклона убывает до 0 и далее становится отрицательным за счет значения 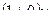 .
.
На рис. ….. фиг. 91 показан характер этих кривых .При 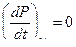 получим соотношение
получим соотношение 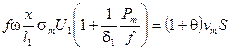 , в момент ….. горения при
, в момент ….. горения при 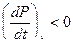 ,
, 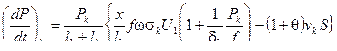
При переходе ко второму периоду выражение для давления имеет вид 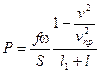 ,
, 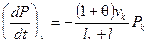 ,
, 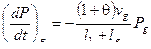 ,
,
Характер нарастания давления в функции от пути –l выразится общей формулой 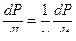 (9.41)
(9.41)
Вначале движения ,когда 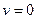 тангенс угла наклона равен ∞ ,т.е. кривая Р(l) будет иметь касательную совпадающую с осью ординат рис.(фиг.92)
тангенс угла наклона равен ∞ ,т.е. кривая Р(l) будет иметь касательную совпадающую с осью ординат рис.(фиг.92)
9.6 Влияние формы и размеров пороха на кривые давления газов и скорости снаряда.
Анализ формул (9.40) и (9.41) показывает ,что характер нарастания давления как во времени так и функции от пути снаряда зависит , главным образом от 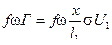 при данной "силе" и природе пороха зависит от
при данной "силе" и природе пороха зависит от 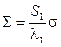
Для простоты , рассмотрим случай когда зёрна имеют одинаковую толщину , но разную форму . Взяв для пяти дегрессивных форм общие формулы и примерные числовые данные имеем таблицу :
| форма зерна | 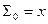
| 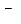
| 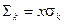
| 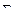
| 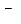
| 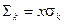
| |
| 1 | трубка | 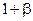
| 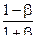
| 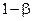
| 1,003 | 0,0994 | 0,997 |
| 2 | лента | 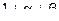
| 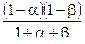
| 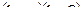
| 1,06 | 0,89 | 0,943 |
| 3 | пластинка | 
| 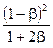
| 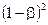
| 1,20 | 0,675 | 0,810 |
| 4 | брусок | 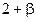
| 0 | 0 | ~2,0 | 0 | 0 |
| 5 | куб | 3 | 0 | 0 | 3 | 0 | 0 |
Нанеся на график изменение 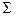 в зависимости от Z получим диаграмму изображенную на рис(фиг.93). На рис(фиг.94) приведены расчеты давлений газов при
в зависимости от Z получим диаграмму изображенную на рис(фиг.93). На рис(фиг.94) приведены расчеты давлений газов при 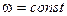 и
и  в функцию от пути . Диаграмма показывает ,что лента дает нормальное давление
в функцию от пути . Диаграмма показывает ,что лента дает нормальное давление 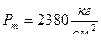 и дульную скорость
и дульную скорость

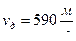
 .Брусок –4 , имея большую начальную оголенность дает давление
.Брусок –4 , имея большую начальную оголенность дает давление 
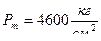 и
и 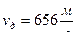 . Куб –5 в следствии втрое большей оголенности имеет давление
. Куб –5 в следствии втрое большей оголенности имеет давление 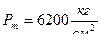 и
и 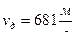 . Если бы поставить задачу : сравнить дульные скорости при одинаковых Рm ,то ленточный порох показал наилучшие результаты .
. Если бы поставить задачу : сравнить дульные скорости при одинаковых Рm ,то ленточный порох показал наилучшие результаты .
Теперь рассмотрим влияние толщины свода при одинаковой форме зерна . Результаты расчетов сведены в таблицу :
2 
| 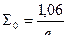
| 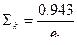
| 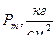
| 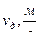
|
| 1,5 | 1,414 | 1,256 | 3540 | 632 |
| 2,0 | 1,06 | 0,943 | 2040 | 575 |
| 2,5 | 0,848 | 0,744 | 1450 | 486 |
Влияние толщины пороха на кривые давления показаны на рис…(фиг.96)
10. Решение основной задачи внутренней баллистики (ОЗВБ).
Установление закономерностей , связывающих разнообразные условия заряжания с зависящими от них величин , называемыми баллистическими элементами выстрела составляет общую задачу внутренней баллистики .
К условиям заряжания относятся : размеры каморы и канала ствола , его вес , устройство нарезка в канале , вес и устройство снаряда ,давление форсирования , зависящее от устройства пояска снаряда и нарезки канала , вес заряда , марка пороха , физико-химические и баллистические пороха , характеристики расширения газов 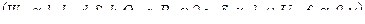 .
.
К баллистическим элементам выстрела относятся : изменяющееся во времени путь снаряда –l, скорость снаряда 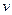 , давление пороховых газов –Р, их температура – Т , а также количество газов
, давление пороховых газов –Р, их температура – Т , а также количество газов 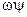 , образовавшиеся к данному моменту ; а также относительная толщина горящего свода –Z.
, образовавшиеся к данному моменту ; а также относительная толщина горящего свода –Z.
При решении указанной выше ОЗВБ можно выделить две важнейших основных задач пиродинамики и ряд частных задач .
Первая основная задача пиродинамики состоит в определении расчетом изменения газов и скорости снаряда в канале ствола в функции от пути снаряда и от времени при заданных условиях заряжания . При этом наряду с кривыми Р(l),υ(l) или P(t),υ(t) и l(t) определяются две важнейшие баллистические характеристики орудия – наибольшее давление газов –Рm в канале ствола и дульная скорость снаряда -  ,т.е. скорость снарыда при вылете его из канала ствола . Эту задачу называют прямой задачей пиродинамики . При заданных условиях заряжания она иееет единственное решение. Изменяя условия заряжания можно провести анализ этих условий на изменение кривых давления газов и скорости снаряда ,т.е. решить ряд частных задач . Точность решения этой задачи зависит от выбранной математической модели выстрела и методов решения . Вторая основная задача пиродинамики – задача баллистического проектирования орудия состоит в определении конструктивных данных канала ствола и условий заряжания , при которых снаряд данного калибра-d и веса-q , получает при вылете определенную дульную скорость -
,т.е. скорость снарыда при вылете его из канала ствола . Эту задачу называют прямой задачей пиродинамики . При заданных условиях заряжания она иееет единственное решение. Изменяя условия заряжания можно провести анализ этих условий на изменение кривых давления газов и скорости снаряда ,т.е. решить ряд частных задач . Точность решения этой задачи зависит от выбранной математической модели выстрела и методов решения . Вторая основная задача пиродинамики – задача баллистического проектирования орудия состоит в определении конструктивных данных канала ствола и условий заряжания , при которых снаряд данного калибра-d и веса-q , получает при вылете определенную дульную скорость -  .Эта скорость задается на основе тактико-технических требований ,предъявляемых к проектируемому орудию . При решении её обычно , задаются наибольшим давлением газов –Рm. Решение этой задачи многовариантно от целесообразности и рациональности выбранного варианта баллистического решения в значительной степени зависит дальнейшее проектирование всей артиллерийской системы в целом и боеприпасов к ней . По выбранным условиям заряжания производится расчет кривых давления и скорости . Полученная кривая Р(t) или P(l) используется конструкторами для расчета прочности стенок орудия и снаряда , лафета ,дистанционных трубок , взрывателей . Вместе с этим даются требуемая толщина и форма пороха , который должен быть изготовлен на заводе .
.Эта скорость задается на основе тактико-технических требований ,предъявляемых к проектируемому орудию . При решении её обычно , задаются наибольшим давлением газов –Рm. Решение этой задачи многовариантно от целесообразности и рациональности выбранного варианта баллистического решения в значительной степени зависит дальнейшее проектирование всей артиллерийской системы в целом и боеприпасов к ней . По выбранным условиям заряжания производится расчет кривых давления и скорости . Полученная кривая Р(t) или P(l) используется конструкторами для расчета прочности стенок орудия и снаряда , лафета ,дистанционных трубок , взрывателей . Вместе с этим даются требуемая толщина и форма пороха , который должен быть изготовлен на заводе .
Здесь возникают специальные частные задачи о нахождении наивыгоднейших решений , от орудий наибольшего могущества , об орудии наименьшей длины или объёма , о наивыгоднейшем заряде и наивыгоднейших условий заряжания .
Методы решения решения задач пиродинамики можно разделить на аналитические , численные , эмпирические и табличные.
В настоящее время , в связи с появлением персональных быстродействующих ЭВМ , все большее значение приобретают численные методы , в которых постановка задачи ставится более шире , чем в других методах решения , но в численных методах используется целый ряд допущений.
Основные допущения при решении ОЗВБ:
1. Горение пороха подчиняется геометрическому закону горения или физическому закону горения.
2. Порох горит при средних давлениях p , воспламенение мгновенное.
3. Состав продуктов горения не меняется (f и 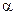 - постоянные).
- постоянные).
4. Скорость горения пороха пропорциональна давлению  .
.
5. Учитываемые второстепенные работы пропорциональны главной работе поступательного движения снаряда и учитываются при помощи коэффициента 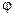 .
.
6. Движение снаряда начинается , когда в каморе в результате сгорания части заряда разовьется давление форсирования –p0 , постепенность врезания в n не учитывается.
7. Работа врезания пояска отдельно не учитывается.
8. Растяжением стенок ствола при выстреле , прорывом газов через зазоры между ведущим пояском и стенками канала ствола и сопротивлением воздуха в канале ствола пренебрегаем.
9. Охлаждение газов в результате теплоотдачи стенкам ствола непосредственно не учитывается и может принято в расчет косвенно , снижением f и увеличением  .
.
10. Движение снаряда рассматривается до момента прохождения его дна через дульный срез.
11. Величину  принимаем равной среднему значению для всего периода выстрела.
принимаем равной среднему значению для всего периода выстрела.
12. Плотность газопороховой смеси зависит только от времени и не зависит от координаты.
Таким образом уравнения классической внутренней баллистики для усредненных значений давлений p, температуры T и относительного количества сгоревшего заряда 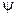 , при этом осреднение T и
, при этом осреднение T и 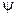 получается как следствие осреднения давления . Иначе говоря , в классическом методе внутренней баллистики волновые процессы течения газа не учитываются , и применяется "термодинамический" закон расширения газов .
получается как следствие осреднения давления . Иначе говоря , в классическом методе внутренней баллистики волновые процессы течения газа не учитываются , и применяется "термодинамический" закон расширения газов .
Этот классический метод расширения дает хорошие результаты для относительно тяжелых снарядов , когда 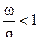 , т.е. когда в области действия первой волны разряжения , снаряд не набирает значительной скорости и первая волна разряжения от дна каморы догоняет снаряд вблизи начала координат , и учет первой волны разряжения будет несущественным , т.к. далее устанавливается "термодинамический" режим расширения пороховых газов .
, т.е. когда в области действия первой волны разряжения , снаряд не набирает значительной скорости и первая волна разряжения от дна каморы догоняет снаряд вблизи начала координат , и учет первой волны разряжения будет несущественным , т.к. далее устанавливается "термодинамический" режим расширения пороховых газов .
Для нахождения элементов выстрела в классическом методе О.З.В.Б. имеем следующие зависимости :
1) 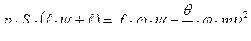 - основное уравнение пиродинамики , уравнение Резаля .
- основное уравнение пиродинамики , уравнение Резаля .
2) 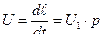 или
или 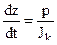 - закон горения пороха .
- закон горения пороха .
3) 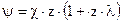 - двухчленный закон газообразования .
- двухчленный закон газообразования .
4) 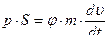 - закон движения снаряда .
- закон движения снаряда .
5) 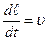 - кинематическая связь между скоростью и путем .
- кинематическая связь между скоростью и путем .
Совокупность этих 5-ти уравнений позволяет найти 5-ть неизвестных p,z,υ,l, 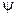 как функции времени.
как функции времени.
10.1 Система уравнений ОЗВБ для пороха простой дигрессивной формы.
Для вычисления элементов выстрела по имеющейся специальной программе, по которой решается система обыкновенных дифференциальных уравнений 1-го порядка на ПЭВМ (macad) приведем наши уравнения к нормализованному виду (система 10,1)
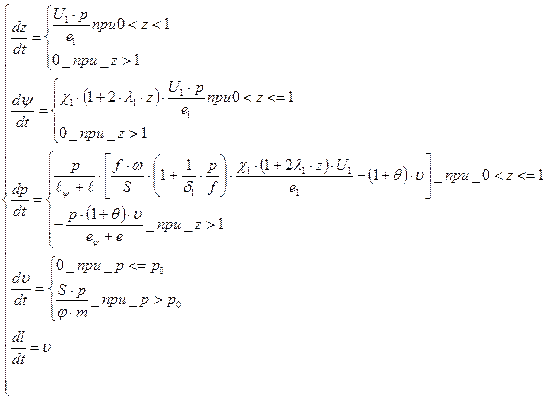 (10,1)
(10,1)
где l  =
= 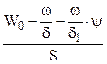 ;
; 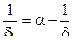 .
.
Система уравнений ( 10,1 ) решается при следующих начальных данных :
при t = 0 , z =0 , 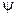 = 0 , p = pв , υ = 0 , l = 0 , конец расчета l = lд .
= 0 , p = pв , υ = 0 , l = 0 , конец расчета l = lд .
Точность и правильность расчета проверяются по аналитическим зависимостям в момент p = p0 :
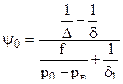
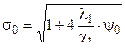
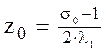
При горении пороха :
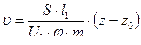
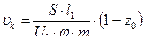
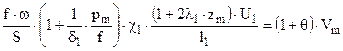
где pm , zm , Vm – значения давления , скорости и относительной толщины в момент максимального давления .
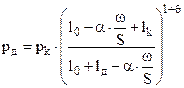
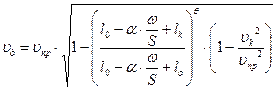
где υпр = 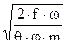
Правильность решения проверяется при различных условиях заряжания в постоянных переменных Н.Ф. Дроздова :
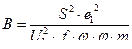
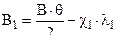
10.2 Системы уравнений для многоканального пороха прогрессивной формы .
При решении ОЗВБ для многоканального пороха воспользуемся двухчленными формулами для 1-й фазы горения ( до распада зерна ) и 2-й фазы горения ( после распада зерна ) . Для 1-й фазы горения характеристики
 и
и  найдутся из условия , что при z = 1
найдутся из условия , что при z = 1 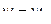 и при z = 0,5 значения
и при z = 0,5 значения 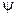 будут совпадать как по трехчленной , так и по двухчленной формулам :
будут совпадать как по трехчленной , так и по двухчленной формулам :
при z=0,5 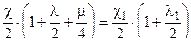
при z=1 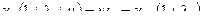
откуда имеем
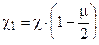 ,
, 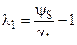
Для второй фазы горения имеем
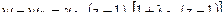
характеристики  и
и  найдутся из условия , что при z=zk
найдутся из условия , что при z=zk  и при
и при
z=zk поверхность горения должна обратиться в ноль . Откуда получим :
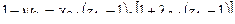
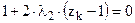
Решая находим эти уравнения: 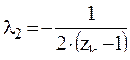
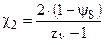
Подсчитав χ и λ по этим формулам для 7-ми канального стандартного пороха имеем :
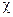 =0,712 ;
=0,712 ;  =0,225 ;
=0,225 ; 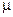 = - 0,0237 ;
= - 0,0237 ; 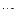 =0,855 ;
=0,855 ;  =1,375 ;
=1,375 ;  ;
;  =0,1873 ;
=0,1873 ;
ошибка  =0,004 .
=0,004 .
Принимая для 7-ми канального пороха наружный радиус вписанного круга в наружную призмочку  0,532е1 получим ек=е1+0,532е1=1,532е1
0,532е1 получим ек=е1+0,532е1=1,532е1
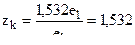 ;
; 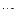 =0,855 ;
=0,855 ;  = - 0,94 ;
= - 0,94 ; 
Для зерна Уолша с 7-ю каналами  ;
; 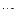 =0,95 ;
=0,95 ;  = - 2,16 ;
= - 2,16 ; 
 =1,37 ;
=1,37 ; 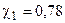 ;
;  =0,218 .
=0,218 .
Исходя из 2-х фаз горения : прогрессивного в первой фазе и дегрессивного во второй фазе система уравнений ( 10,2 ) будет иметь следующий вид
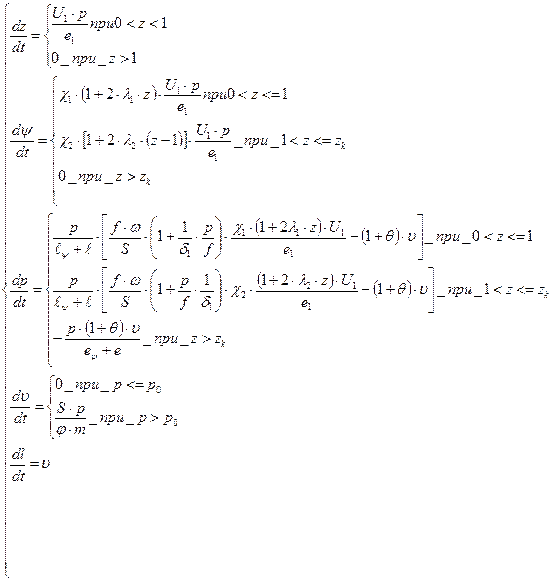 (10.2)
(10.2)
где 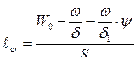 ;
; 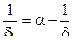
Система ( 10,2 ) решается при следующих начальных данных : при t = 0 , z=0, 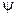 =0 , p = pв , l = 0 , υ= 0 . Расчет заканчивается при l = lд . Точность и правильность расчета проверяется как при расчете системы ( 10,1 ) .
=0 , p = pв , l = 0 , υ= 0 . Расчет заканчивается при l = lд . Точность и правильность расчета проверяется как при расчете системы ( 10,1 ) .
10.3 Системы уравнений для комбинированного заряда из дегрессивных порохов простой формы .
Пусть комбинированный заряд состоит из n порохов дегрессивной простой формы . Характеристики i-того пороха обозначим с индексом i , так что
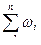 , где i =1...n .
, где i =1...n .
Весовую долю каждого пороха обозначим через 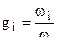 , тогда по правилу смешения можно найти фиктивный эквивалентный порох , имеющий такие же характеристики как комбинираванный пороховой заряд :
, тогда по правилу смешения можно найти фиктивный эквивалентный порох , имеющий такие же характеристики как комбинираванный пороховой заряд :
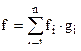 ;
; 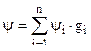 ;
; 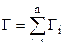 ;
; 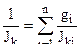 ;
; 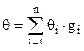
Расставив пороха по импульсу в конце горения , пороха по возрастающему значению J1<Ji<Jn и воспользовавшись системой уравнений ( 10,1 ) окончательно получим
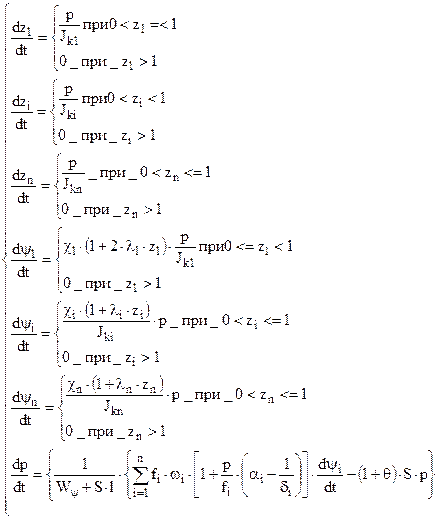 ( 10,3 )
( 10,3 )
где 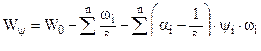
Точность решения системы уравнений проверяется по аналитическим зависимостям , по которым проверяется точность системы ( 10,1 ) . При этом необходимо брать характеристики эквивалентного фиктивного пороха f , Jk ,
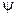 , Г ,
, Г ,  ,
, 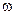 , формулы которых приведены выше . Значения
, формулы которых приведены выше . Значения 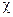 и
и 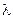 такого пороха определяются по формулам ( 10,4 )
такого пороха определяются по формулам ( 10,4 )
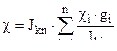
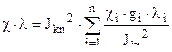 ( 10,4 )
( 10,4 )
Уравнение газообразования примет вид :
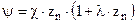 ( 10,5 )
( 10,5 )
10.4 Системы уравнений для комбинированного заряда , состоящего из 7-ми канального и трубчатого порохов .
В артиллерийских орудиях среднего и крупного калибра пороховой заряд состоит из центрального пучка , содержащего трубчатый порох , заданного по чертежу веса , вокруг которого размещается в ... картузе переменный заряд 7-ми канального пороха того же состава .
При приемке партии варьируется вес только зерненного пороха . Ниже приведена система уравнений для такого комбинированного заряда .
Пусть трубчаты порох имеет индекс – Т . 7-ми канальный имеет обозначения такие же как в системе ( 10,2 ) . ОЗВБ для такого заряда решается по системе уравнений ( 10,6 ) :
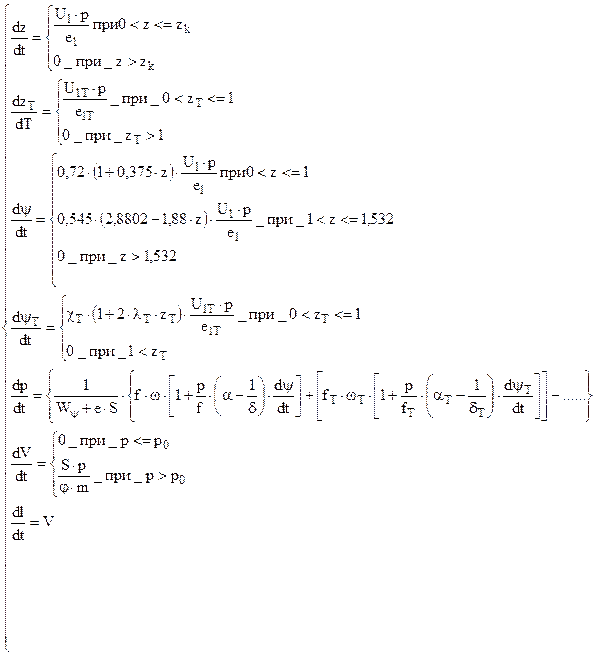 (10,6 )
(10,6 )
Фиктивный порох эквивалентный комбинированному заряду имеет следующие баллистические характеристики :
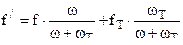
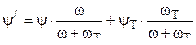
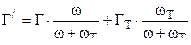
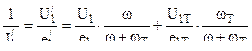
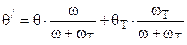
1) 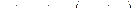 при
при 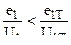 где
где
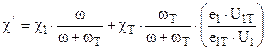
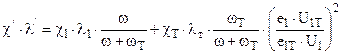
2) или 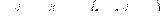 при
при 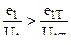 где
где
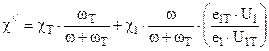
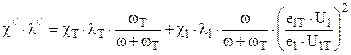
Точность решения системы проверяется по аналитическим зависимостям , представленным выше , которые справедливы в 1-м случае – до распада зерна 7-ми канального пороха , во втором случае – до конца горения трубчатого пороха , который наступает раньше распада зерна .
10.5 Исходная система уравнений внутренней баллистики для миномётов, орудий и ракет.
Рассмотрим систему уравнений , базирующуюся на единой теплофизической модели для различных по схемам действия и конструктивному оформлению орудий ( классическое артиллерийское орудие , динамо реактивные системы , РДТТ и другие ) . Впервые , это важное с методической и практической точек зрения , придложение было высказано и реализовано профессором Б.В. Орловым .
За основу исследований при выводе системы уравнений принимаем частично уравновешенное орудие рис... , для которого справедливо соотношение :
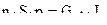 ( 2,13 )
( 2,13 )
где n – коэффициент уравновешенности ; S – площадь поперечного сечения канала ствола с учетом нарезов ; p – баллистическое давление ( среднее давление газов в за снарядном пространстве в данный момент времени ) ; Gp1- расход газов через сопловой блок орудия , имеющий размерность "кг/с" ;
Jr – удельный импульс , развиваемый пороховыми газами при истечении из сопла .
Величина коэффициента уравновешенности "n" ограничена пределами 0<=n<=1 . Для классического артиллерийского орудия n = 0 , для безоткатного n =1 .
Будем полагать так же , что имеет место прорыв пороховых газов через ведущее устройство снаряда , количественно характеризующееся расходом
Gp2 , а так же имеется теплоотдача стенкам канала ствола , и стенка ствола расширяется упруго при выстреле .
Исходную систему уравнений запишем при следующих допущениях :
1. Горение пороха происходит параллельными слоями , т.е. справедливо уравнение газоприхода 
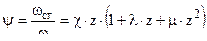 и относительную поверхность горения :
и относительную поверхность горения : 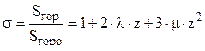 где
где
 - характеристики формы пороха ; z =
- характеристики формы пороха ; z = 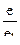 - относительная толщина сгоревшего пороха ; e1 – половина толщины порохового зерна ; e – толщина слоя сгоревшего пороха ;
- относительная толщина сгоревшего пороха ; e1 – половина толщины порохового зерна ; e – толщина слоя сгоревшего пороха ; 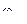 - сгоревшая часть порохового заряда ;
- сгоревшая часть порохового заряда ; 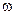 - вес заряда ; Sгор – горящая поверхность заряда ; Sгоро – начальная поверхность заряда .
- вес заряда ; Sгор – горящая поверхность заряда ; Sгоро – начальная поверхность заряда .
2. Давление p , температура Т и плотность газопороховой смеси 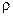 в заснарядном пространстве для каждого момента времени t равны их среднему по объему значениям ( гипотеза квазистационарного процесса ) .
в заснарядном пространстве для каждого момента времени t равны их среднему по объему значениям ( гипотеза квазистационарного процесса ) .
p , T и 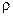 связаны уравнением состояния :
связаны уравнением состояния :
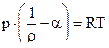
где R – газовая постоянная ; 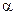 - коволюм газа .
- коволюм газа .
3. Состав продуктов сгорания не меняется во время выстрела , а удельные теплоемкости Cp , C  равны их средним значениям для всего диапазона изменения температур .
равны их средним значениям для всего диапазона изменения температур .
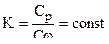 и
и 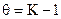 = const .
= const .
4. Воспламенение порохового заряда происходит мгновенно .
5. Отсутствует выброс несгоревших частиц пороха .
6. Противодавлением воздуха в канале ствола пренебрегаем .
При выводе системы уравнений используем основные законы термодинамики :
закон сохранения энергии – первого закона термодинамики запишем в виде :
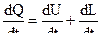
здесь 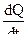 - скорость изменения тепла в газе , вес которого , к рассматриваемому моменту времени составит
- скорость изменения тепла в газе , вес которого , к рассматриваемому моменту времени составит  , вследствие его взаимодействия с окружающей средой .
, вследствие его взаимодействия с окружающей средой .
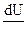 - скорость изменения внутренней энергии газа , где U=
- скорость изменения внутренней энергии газа , где U= 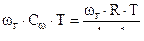 (2,15)
(2,15)
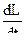 - мощность , развиваемая газом при его расширении или при сжатии .
- мощность , развиваемая газом при его расширении или при сжатии .
Применительно к периоду движения снаряда при горящем заряде :
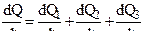 ( 2,16 )
( 2,16 )
Здесь 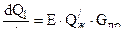 - скорость подвода тепла вследствие сгорания порохового зерна , где Е = 4270
- скорость подвода тепла вследствие сгорания порохового зерна , где Е = 4270 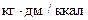 - механический эквивалент тепла;
- механический эквивалент тепла;
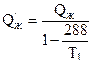
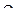 - калорийность пороха при воде жидкой , т.к.
- калорийность пороха при воде жидкой , т.к. 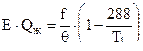 .
.
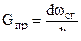 - приход продуктов сгорания .
- приход продуктов сгорания .
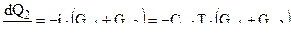 - скорость оттока тепла из каморы орудия в атмосферу вследствие истечения газов через сопло ( Gp1 ) и в зазоры между ведущими устройствами снаряда и стенками канала ствола ( Gp2 ) .
- скорость оттока тепла из каморы орудия в атмосферу вследствие истечения газов через сопло ( Gp1 ) и в зазоры между ведущими устройствами снаряда и стенками канала ствола ( Gp2 ) .
 - энтальпия одного кг газа .
- энтальпия одного кг газа .
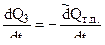 - скорость изменения тепла в следствие теплоотдачи между стенками ствола и газами ( символ
- скорость изменения тепла в следствие теплоотдачи между стенками ствола и газами ( символ 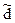 показывает , что
показывает , что 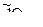 не является полным дифференциалом ) .
не является полным дифференциалом ) .
Скорость отвода тепла из-за снарядного пространства в стенке канала ствола:
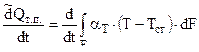 ( 2,17 )
( 2,17 )
где  - коэффициент теплоотдачи от газа к стенкам ; Тсг – температура внутренней поверхности ствола ; F – поверхность , омываемая газами .
- коэффициент теплоотдачи от газа к стенкам ; Тсг – температура внутренней поверхности ствола ; F – поверхность , омываемая газами .
Точно уравнение ( 2,17 ) решается совместно с уравнением теплопроводности материала стенки при соответствующих краевых условиях. Величина 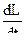 в общем случае выражается уравнением :
в общем случае выражается уравнением :
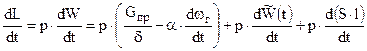 ( 2,18 )
( 2,18 )
Здесь W – свободный объем за снарядного пространства ;
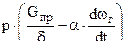 - мощность , создаваемая газом , вследствие сгорания заряда с учетом истечения части газа из за снарядного пространства , где
- мощность , создаваемая газом , вследствие сгорания заряда с учетом истечения части газа из за снарядного пространства , где 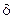 - удельный вес пороха ;
- удельный вес пороха ;
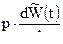 - мощность , затрачиваемая на упругие деформации стенок , гильзы и ствола , где
- мощность , затрачиваемая на упругие деформации стенок , гильзы и ствола , где  - "упругое" приращение за снарядного объема . Обычно этой мощностью пренебрегают , хотя в пушках высоких давлений она может являться ощутимой ( ППН,ЛГУ ) .
- "упругое" приращение за снарядного объема . Обычно этой мощностью пренебрегают , хотя в пушках высоких давлений она может являться ощутимой ( ППН,ЛГУ ) .
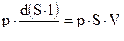 ( 2,19 )
( 2,19 )
Мощность расходуемая на поступательное движение снаряда с фиктивным весом 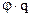 , где q – вес снаряда ,
, где q – вес снаряда , 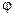 - коэффициент фиктивности или коэффициент , учитывающий поступательное движение снаряда , его вращение , преодоление вредных сопротивлений , откат откатных частей , выталкивание столбов воздуха и , наконец , работу на перемещение газопороховой смеси .
- коэффициент фиктивности или коэффициент , учитывающий поступательное движение снаряда , его вращение , преодоление вредных сопротивлений , откат откатных частей , выталкивание столбов воздуха и , наконец , работу на перемещение газопороховой смеси .
Обычно в расчетах 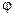 принимается постоянным :
принимается постоянным :
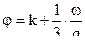 ( 2,20 )
( 2,20 )
где к зависит от калибра и начальной скорости снаряда и типа снаряда .
С уменьшением калибра снаряда величина "к" – возрастает и уменьшается с ростом начальной скорости . Для снаряда с ведущим пояском "к" = 1,02-1,05.
Для пуль , имеющих калибр меньше 14,5 мм и не имеющих ведущего пояска
"к"=1,2-1,3 .
С учетом выражений ( 2,15 ) , ( 2,16 ) , ( 2,18 ) уравнение сохранения энергии применительно к рассматриваемой схеме ( рис... ) приводится к виду :
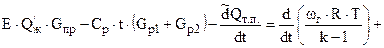
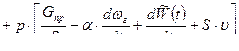 ( 2,21 )
( 2,21 )
Соотношение ( 2,21 ) так же называют основным уравнением внутренней баллистики . Уравнение сохранения вещества может быть записано в виде
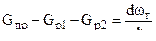 ( 2,22 )
( 2,22 )
Приход газов в следствии сгорания пороха 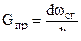 определяется по формуле
определяется по формуле
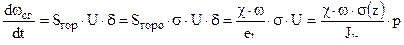 ( 2,23 )
( 2,23 )
Значения Gp2 , Gp1 зависят от значений полной температуры T00 и полного давления газов p00 в за снарядном пространстве , а так же площадей критических сечений сопла  и зазор Fз . При расчете Gp2 следует дополнительно учитывать скорости снаряда и формы зазоров во времени
и зазор Fз . При расчете Gp2 следует дополнительно учитывать скорости снаряда и формы зазоров во времени
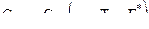
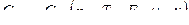
 - коэффициент расхода , который учитывает особенности истечения пороховых газов через появившийся зазор и определяется экспериментально член
- коэффициент расхода , который учитывает особенности истечения пороховых газов через появившийся зазор и определяется экспериментально член 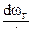 - скорость изменения количества газов в за снарядном пространстве . Уравнение движения снаряда :
- скорость изменения количества газов в за снарядном пространстве . Уравнение движения снаряда :
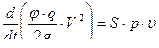 или
или 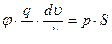 ( 2,25 )
( 2,25 )
Уравнение состояния :
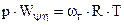 где
где
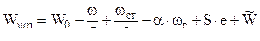
где
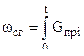
Для решения основной задачи внутренней баллистики должны быть известны законы скорости горения пороха U=Up и изменения поверхности порохового зерна в функции толщины горения свода е ( или z ) . Таким образом параметры состояния газа , а так же скорость и путь снаряда до момента вылета его из ствола могут быть найдены из следующей системы уравнений :
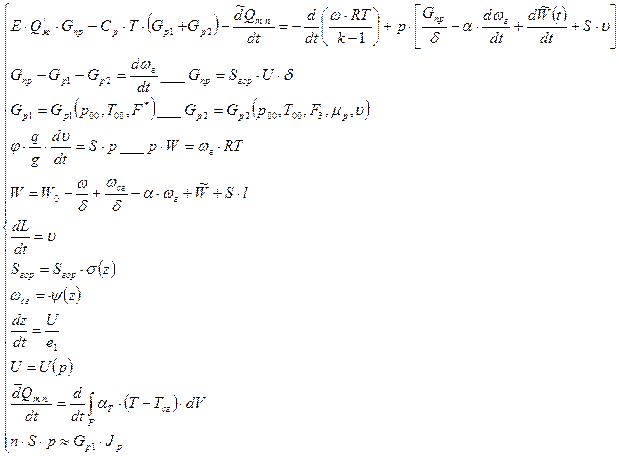 (2,26)
(2,26)
Накладывая определенные ограничения , с помощью полученной системы уравнений (2.26) можно описать процессы выстрела в следующих системах:
1. Безоткатные орудия (n=1).
2. Миномет (n=0 , Gp1=0).
3. Классическое орудие (n=0 , Gp1=0 , Gp2=0).
4. Ракетный двигатель (Gp2=0 , υ=0).
5. Бомба постоянного объема ( Gp1=0 , Gp2=0 , υ=0).
Если параметры состояния газов определяются после окончательного горения заряда в системе (2.26) необходимо положить Sгор=0 и U=0.
После вылета снаряда из канала ствола расчет продолжается при Sгор=0 и U=0 и Fз=S и из системы (2.26) исключается уравнение движения снаряда.
Внутренняя баллистика классического орудия.
Для закона сохранения энергии , когда Gp1=0 , Gp2=0 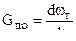 в момент горения пороха будем иметь:
в момент горения пороха будем иметь:
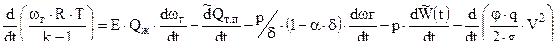 (2.27).
(2.27).
В предварительном периоде горения пороха идет при υ=0 и l=0 до момента p=p0 и 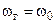 , где p0- давление форсирования снаряда;
, где p0- давление форсирования снаряда;
 количество газа , образовавшегося в момент t=t0 – форсирования снаряда. Интегрируя уравнение (2.27) получим:
количество газа , образовавшегося в момент t=t0 – форсирования снаряда. Интегрируя уравнение (2.27) получим:

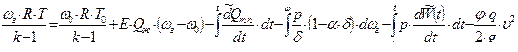 ( 2,28 )
( 2,28 )
На 2-м периоде – периоде расширения пороховых газов ( Sгор = 0 , U = 0 ,
 ) , уравнение сохранения энергии примет следующий вид :
) , уравнение сохранения энергии примет следующий вид :
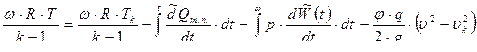
Для предварительного периода ( υ = 0 ) получим
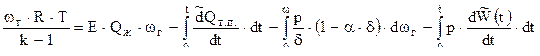
Для приближенного учета теплоотдачи 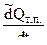 воспользуемся допущением , согласно которому процесс теплоотдачи можно считать квазистационарным,
воспользуемся допущением , согласно которому процесс теплоотдачи можно считать квазистационарным,
с коэффициентом теплоотдачи – линейно зависящим от удалённого веса газа 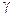 в за снарядном пространстве
в за снарядном пространстве
 ( 2,29 )
( 2,29 )
где  - постоянный коэффициент теплоотдачи . Т.к.
- постоянный коэффициент теплоотдачи . Т.к. 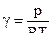 , то
, то
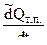 =
= 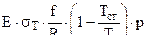
Введем обозначение 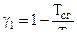 , тогда
, тогда
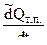 =
= 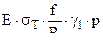 ( 2,30 )
( 2,30 )
Значение  находятся из экспериментов . Для автоматических пушек допустимо принимать
находятся из экспериментов . Для автоматических пушек допустимо принимать 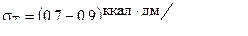 ,
, 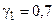 . С учетом этого допущения система ( 2,26 ) примет вид :
. С учетом этого допущения система ( 2,26 ) примет вид :
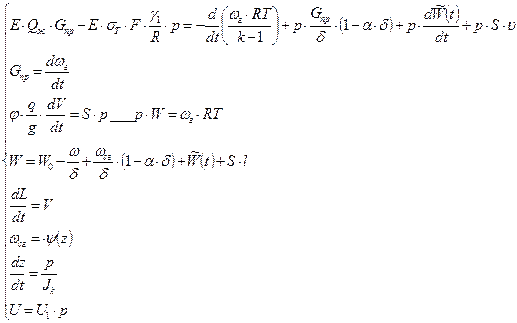 ( 2,31 )
( 2,31 )
где Jk = 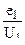
Учитывая , что 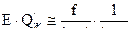
где f – сила пороха , 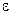 - доля твердых остатков в продуктах сгорания ( для дымных порохов
- доля твердых остатков в продуктах сгорания ( для дымных порохов 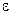 = 0,5 ; для бездымных порохов
= 0,5 ; для бездымных порохов 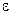 = 0 ).
= 0 ).

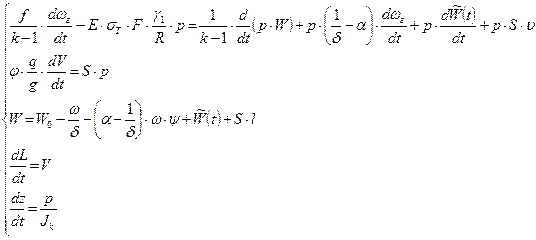 ( 2,32 )
( 2,32 )
где 
т.к. 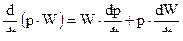 и
и
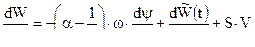 то получим
то получим
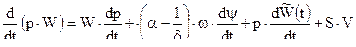 ( 2,33 )
( 2,33 )
Подставляя выражение ( 2,33 ) в первое уравнение системы ( 2,32 ) окончательно получим :
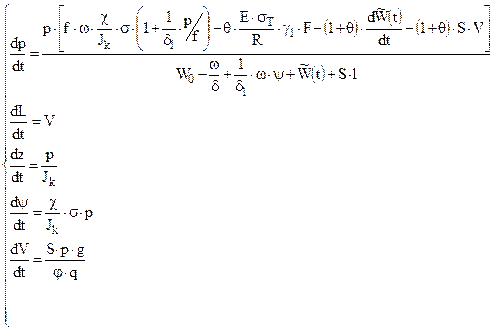 ( 2,34 )
( 2,34 )
где F = S0 + 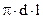
 ;
; 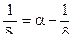
Если пренебречь растяжением стенок ствола ( 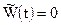 ) окончательно получим систему уравнений с учетом теплоотдач :
) окончательно получим систему уравнений с учетом теплоотдач :
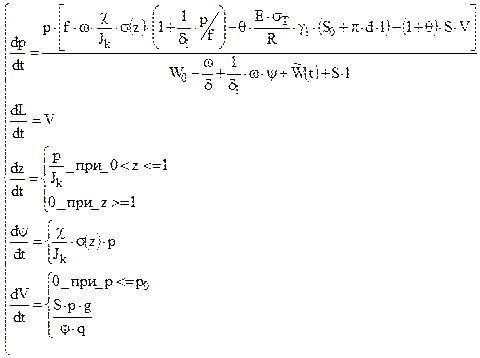 ( 2,35 )
( 2,35 )
где 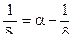 ;
; 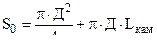
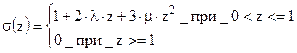
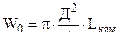 .
.
Рассмотрим учет теплоотдачи при выстреле предложенный Мюрауром для бомбы , принимая во внимание постепенное возрастание охлаждающей поверхности стенки :
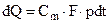 ( 2,36 )
( 2,36 )
где Cm – экспериментально найденный коэффициент в бомбе при сжигании дымного пороха по времени сгорания его при 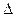 = 0,2 кг/дм3 .
= 0,2 кг/дм3 .
Имеется кривая Cm=Cm(tk) или таблица , по которой Cm можно определить .
С другой стороны имеем :
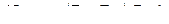 ( 2,37 )
( 2,37 )
Согласно формуле профессора Мамонтова М.А.
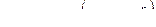 ( 2,38 )
( 2,38 )
где  - коэффициент теплопередачи для газов при U = 0 .
- коэффициент теплопередачи для газов при U = 0 .
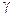 - плотность пороховых газов
- плотность пороховых газов
U – скорость течения газов у стенки
n – показатель степени : n = 0,5-1
 - скоростной коэффициент , определяемый из опытов .
- скоростной коэффициент , определяемый из опытов .
Сравнивая ( 2,36 ) и ( 2,37 ) получим :
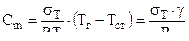 ( 2,39 )
( 2,39 )
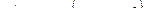
Коэффициент Cm/ учитывает скорость течения пороховых газов в орудии .
В мfнометрической бомбе U=0 и Cm/ = Cm ,тогда
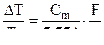 ( 2,41 )
( 2,41 )
где 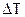 - потеря температуры пороховых газов за счет теплоотдачи ;
- потеря температуры пороховых газов за счет теплоотдачи ;
T1 – температура горения пороха ;
7,774 – переходной коэффициент от бомбы Мюраура к нашим условиям .
Поверхность теплоотдачи F = 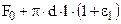 ( 2,42 )
( 2,42 )
где F0 = 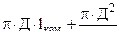 - поверхность каморы орудия ;
- поверхность каморы орудия ;
lкам – длина каморы ;
Д – диаметр каморы ;
d – диаметр канала ствола ;
l – пройденный путь снарядом в канале ствола ;
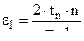 - коэффициент , учитывающий поверхность граней нарезов ;
- коэффициент , учитывающий поверхность граней нарезов ;
tn – глубина нарезов ;
n – число нарезов .
Объем каморы
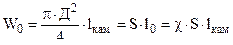 где
где
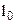 - приведенная длина каморы ;
- приведенная длина каморы ;
S- площадь сечения ствола ;
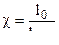 - уширение каморы .
- уширение каморы .
Учитывая , что сила пороха f = RT1 , то введя значение f1 = 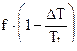 (2,43)
(2,43)
мы придем к системе уравнений имеющей вид ( 11,1 ) принимает вид системы ( 2,44 )
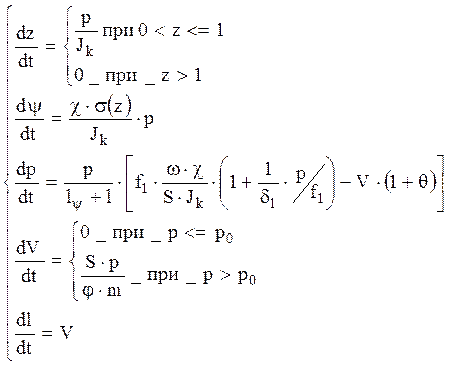 ( 2,44 )
( 2,44 )
где 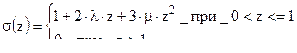
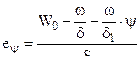 ;
; 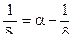
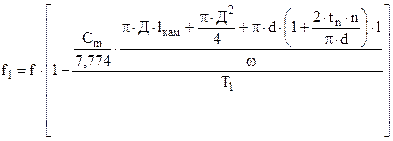
W0 = 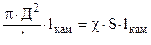
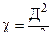 ;
; 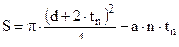 ;
; 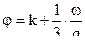
Начальные условия :
при t = 0 , p = pв , V = 0 , l = 0 , 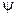 = 0 , z = 0 .
= 0 , z = 0 .
Расчет ведется до l = lд . Шаг интегрирования не более
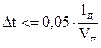 и уточняется в процессе расчета .
и уточняется в процессе расчета .
Входными данными являются :
Параметры ствола – Д , lкам , d , tn , a , n , lд .
Параметры снаряда – q , p0 .
Параметры порохового заряда - 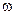 .
.
Марка пороха : 2е1 , 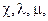 или Jк ,
или Jк , 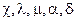 .
.
Коэффициент фиктивности 
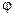 или k :
или k : 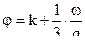
10.6 Баллистическое проектирование артиллерийских стволов .
Задача обычно расчленяется на две части :
1. Устанавливается калибр орудия , тип снаряда и его начальная скорость , обеспечивающая решение поставленной боевой задачи .
2. Определяются размеры канала ствола и характеристики заряда .
Первая часть задачи имеет сравнительно мало вариантов решения , т.к. ТТТ обычно более или менее однозначно определяют вес снаряда , что в свою очередь определяет калибр системы и начальную скорость снаряда .Решение второй части баллистического проектирования имеет множество вариантов и отыскание наилучшего без хорошей методики потребует значительного времени .
В качестве основного метода решения обратной задачи внутренней баллистики обычно используется табличный метод , позволяющий достаточно быстро определить все параметры интересующего варианта . В последние годы для решения этой задачи используется ПЭВМ .
10.5.1. Порядок баллистического проектирования артиллерийского ствола .
1. В соответствии с ТТТ устанавливается вес снаряда q , калибр системы , начальная скорость снаряда V0 . Вес и кинетическая энергия снаряда определяются из условия поражения цели , калибр желательно брать равным одному из существующих . По расстоянию до цели и энергии снаряда у цели определяется начальная скорость ( задача внешней баллистики ) .
2. Определяются исходные данные для баллистического решения , с этой целью вычисляется дульная энергия снаряда – Ед :
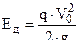
Коэффициент могущества – CE :
CE = 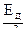
причем величина дульной скорости принимается равной начальной скорости Vд = V0 , т.е. с небольшим запасом на импульс после действия пороховых газов . Величина CЕ определяет в первом приближении исходные данные системы . Профессор В.Е. Слухоцкий , проанализировав большое число артиллерийских систем установил приближенные зависимости между коэффициентом могущества CЕ и основными характеристиками орудия . Результаты этого исследования приведены в таблице .
CЕ , 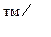
|  , ,
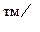
| pm ,
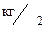
| 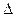 , ,
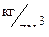
| 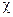
| lд , клб. | CЕ , 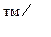
|  , ,
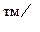
| pm ,
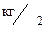
| 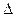 , ,
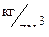
| 
| lд , клб |
| 100 | 124 | 1700 | 0,5 | 1,02 | 14 | 900 | 106 | 3250 | 0,69 | 1,85 | 71 |
| 200 | 120 | 1950 | 0,55 | 1,09 | 23 | 1000 | 105 | 3350 | 0,69 | 1,98 | 78 |
| 300 | 117 | 2200 | 0,59 | 1,18 | 31 | 1100 | 104 | 3450 | 0,70 | 2,11 | 85 |
| 400 | 114 | 2400 | 0,62 | 1,28 | 38 | 1200 | 104 | 3550 | 0,71 | 2,25 | 91 |
| 500 | 112 | 2600 | 0,64 | 1,39 | 44 | 1300 | 103 | 3650 | 0,71 | 2,40 | 98 |
| 600 | 110 | 2800 | 0,66 | 1,50 | 51 | 1400 | 103 | 3750 | 0,72 | 2,57 | 105 |
| 700 | 108 | 2950 | 0,67 | 1,61 | 57 | 1500 | 102 | 3900 | 0,73 | 2,75 | 112 |
| 800 | 107 | 3100 | 0,68 | 1,73 | 64 | 1600 | 102 | 4000 | 0,74 | 2,95 | 119 |
В таблице помещены значения максимального давления газов в канале ствола , измеряемого крешерным прибором , коэффициента использования заряда -  и коэффициента уширения каморы -
и коэффициента уширения каморы - 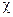 , а так же длинна ствола в калибрах . Расчетное значение в ТБР определяется по зависимости :
, а так же длинна ствола в калибрах . Расчетное значение в ТБР определяется по зависимости :
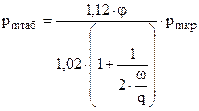
В связи с повышением качества ствольной стали установление с помощью таблицы ( ) значение pmкр следует увеличить примерно на 10-15% .
3. Установление изменения исходных данных .
Верхнее значение исследуемой плотности заряжания рекомендуется брать близким к величине , при которой получается орудие наименьшего объема .
Рекомендуемые значения плотностей заряжания 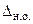 М.Е. Серебряковым и М.С. Гороховым приведены в таблице .
М.Е. Серебряковым и М.С. Гороховым приведены в таблице .
| пороха | pm кг/см2 |
кг/дм3 | |||||
| 2000 | 2400 | 2800 | 3200 | 3600 | 4000 | ||
| лента | 0,53 | 0,6 | 0,66 | 0,71 | 0,76 | 0,8 | 1,1 |
| трубка | 0,54 | 0,62 | 0,68 | 0,73 | 0,77 | 0,82 | 1,0 |
| 7-ми кан. | 0,66 | 0,74 | 0,78 | 0,84 | 0,88 | 0,93 | 1,35 |
Значения коэффициента использования заряда  в орудиях наименьшего объема приведены в таблице .
в орудиях наименьшего объема приведены в таблице .
| CЕ , тм/дм3 | 100-1000 | 1200 | 1400 | 1600 |
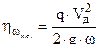
| 86 | 85 | 84 | 83 |
Орудие наименьшего объема оказывается реально приемлемым лишь при
V0 > 1300 м/с . При меньших начальных скоростях следует отойти от него , увеличивая  , т.е. увеличивая длину ствола . Таким образом
, т.е. увеличивая длину ствола . Таким образом 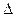 берется в пределах , указанных в таблицах .
берется в пределах , указанных в таблицах .
Зная 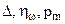 нетрудно получить все исходные параметры по формулам :
нетрудно получить все исходные параметры по формулам :
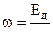 ,
, 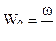 ,
, 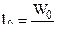 ,
, 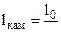 ,
, 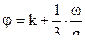 ,
,
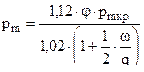 ,
, 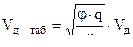 .
.
Профессор М.Е. Серебряков для установления вариантов решения предлагает использовать специальный график 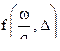 называемый директивной диаграммой рис... Центром графика является точка с координатами
называемый директивной диаграммой рис... Центром графика является точка с координатами 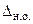 и
и 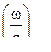 , соответствующего орудия наименьшего объема .
, соответствующего орудия наименьшего объема .
Вокруг центра диаграммы располагаются кривые , отвечающие равным объемам канала ствола . Справа график ограничивает наклонная линия , отвечающая сгоранию заряда в сечении дульного среза . Все реальные варианты находятся слева от этой линии . Директивная диаграмма показывает , в каком направлении следует идти , чтобы получить желаемое изменение баллистических характеристик ствола .
При проектировании систем малого калибра , следует обратить внимание на то , что эти системы имеют большую плотность заряжания 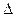 = 0,8-0,9 кг/дм3 , при которых сокращаются габариты и вес патрона , что облегчает проектирование механизмов автоматики . Такие плотности заряжения обеспечиваются применением мелких трубчатых или 7-ми канальных или сферических порохов .
= 0,8-0,9 кг/дм3 , при которых сокращаются габариты и вес патрона , что облегчает проектирование механизмов автоматики . Такие плотности заряжения обеспечиваются применением мелких трубчатых или 7-ми канальных или сферических порохов .
4. Расчет вариантов .
В каждом варианте необходимо определить длину нарезной части и полную длину ствола с затвором , а так же примерное число выстрелов за время баллистической жизни ствола . Первая часть легко решается с помощью ТБР по величинам pm таб и Vд таб при данном 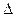 ( или решается система уравнений 10,1 или 10,2 ) .
( или решается система уравнений 10,1 или 10,2 ) .
lств=lд+lкам+(1-2)d
Для оценки живучести можно использовать упрощенную формулу профессора В.Е. Слухоцкого :
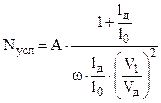 , где
, где
Nусл – живучесть ствола ; A – постоянный коэффициент для всех вариантов ;
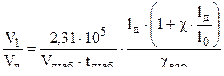
где tдтаб – время выстрела ; 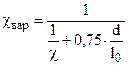
5. Сравнение вариантов и выбор лучшего .
При анализе вариантов необходимо учитывать ТТТ и ряд факторов , если они в ТТТ не заданы , среди которых следует отметить эксплутационные качества системы ( длина и вес ствола , габариты и вес патрона , дульное давление ) . Экономичность системы ( стоимость заряда , стоимость ствола), срок службы системы ( баллистическую живучесть) , технологичность , взаимозаменяемость , уширяемость и др. Многие баллистики занимались критериями выбора вариантов . В частности профессор В.Е. Слухоцкий на основании опыта Великой Отечественной Войны предлагает оценить варианты по величине :
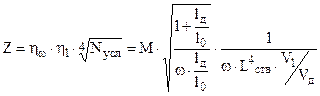
где M = const , кратное десяти .
Лучший вариант , у которого Z наибольшая , однако критерии все базируются на уровне развития артиллерийской техники и во многом образуют взгляды данного периода .По этому они пересматриваются и корректируются . В настоящее время желательно иметь критерии для каждого вида артиллерии отдельно ( зенитная , полевая , танковая и т.д. ) .
6. Уточненный расчет выбранного варианта и построение кривых
p(l) , V(l) , t(l) .
7. Рассчет ствола на прочность .
Для этого найти кривую наибольших давлений на систему ствола , построенную при 3-х температурах заряда t0max заряда , t0нор.зар. и t0min.зар. .
При построении огибающих используется связь между средним давлением на дно канала и на дно снаряда
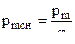 и
и 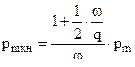
11. Газодинамический метод решения ОЗВБ.
Рассмотрим более подробно основной период , который начинается в момент движения снаряда . Как только снаряд начнет ( предполагая его движение вправо ) двигаться , по горящему пороху пойдет справа налево волна разряжения . Поскольку при горении пороха образуются газы , то можно говорить о распространении волны разряжения по газопороховой смеси . При этом должны наблюдаться две волны , одна из которых с большей скоростью распространения по газу , другая , с меньшей скоростью, по еще несгоревшему пороху . Первая волна разряжения дойдя до неподвижной газопороховой смеси просигнализирует о том , что правее началось движение этой смеси , поскольку снаряд уже начал двигаться . При этом частицы смеси так же вовлекаются в движение . Существенно заметить , что вторая волна , идущая с меньшей скоростью , не существенно изменит режим движения , и ее в дальнейшем не будем учитывать . Волна разряжения , через некоторое время в момент t = 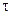 дойдет до неподвижной стенки ( дна каморы ) от нее отразится и пойдет направо , догоняя снаряд .
дойдет до неподвижной стенки ( дна каморы ) от нее отразится и пойдет направо , догоняя снаряд .
Т.к. волны , равносильно малым возмущениям , распространяется как вправо , так и влево с местной скоростью звука – c по отношению подвижного наблюдателя , двигающегося со скоростью движения газа – U (вправо) . Закон движения волн , идущих направо , относительно неподвижного наблюдателя ( например стенки ствола ) будет :
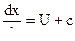 ,
,
а скорость движения волн , идущих налево будет :
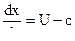 .
.
В зависимости от скорости движения снаряда , длины ствола , длины каморы могут быть различные случаи взаимодействия отраженной волны от дна каморы и дном снаряда .
1-й случай .Скорость снаряда стала на столько велика и ствол очень короткий , что отраженная волна от дна каморы не успевает догнать снаряд и отраженная волна , дойдя до дульного среза констатирует , что снаряд вылетел из ствола .
2-й случай . Скорость снаряда стала велика , но ствол длинный , то отраженная волна успевает догнать снаряд и отразившись от дна не может двигаться влево по отношению неподвижного наблюдателя ( U>c ) и тем самым не сможет достигнуть дна каморы второй раз .
3-й случай . Скорость снаряда мала , а ствол достаточно длинен , что отраженная от дна каморы волна догоняет снаряд , отразившись от дна снаряда успевает достигнуть дна каморы , снова отразившись от дна каморы может второй раз догнать снаряд .Такое многократное отражение волны , когда скорость снаряда U<c приводит к нивелированию характеристик течения газа , когда можно будет считать , что средняя плотность газа в за снарядном пространстве будет падать обратно пропорционально объему этого пространства , а давление с плотностью будет связано законом изэнторы ( адиабаты ) , т.е. установится "термодинамический" режим расширения продуктов сгорания . Этот случай и описывают уравнения систем ( 10,1 ; 10,2 ; 10,3 ; 10,6 ) при решении ОЗВБ при допущении что параметры газа ( p , T , 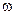 ) в за снарядном пространстве не зависят от координаты сечения , т.е. являются функциями только времени и одинаковы по всему за снарядном пространстве .
) в за снарядном пространстве не зависят от координаты сечения , т.е. являются функциями только времени и одинаковы по всему за снарядном пространстве .
В отличии от "термодинамического" режима течения газа в газодинамическом методе решения ОЗВБ это допущение снимается , т.е. параметра газа ( p , T , 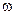 ) и скорость течения – U и скорость звука в газе – с зависят не только от времени , но и от координаты за снарядного пространства . Строгая постановка этой задачи приводит к осемметричному движению газопороховой смеси . Однако , учитывая , что объем переходного конуса по сравнению с объемом цилиндрической части каморы и цилиндро–конического канала ствола и толщина пограничного слоя пороховых газов , прилегающих к стенкам каморы и канала ствола , мала по сравнению с диаметрами . Решение можно искать в одномерной постановке, т.е. предполагая , что параметры газа ( p , T ,
) и скорость течения – U и скорость звука в газе – с зависят не только от времени , но и от координаты за снарядного пространства . Строгая постановка этой задачи приводит к осемметричному движению газопороховой смеси . Однако , учитывая , что объем переходного конуса по сравнению с объемом цилиндрической части каморы и цилиндро–конического канала ствола и толщина пограничного слоя пороховых газов , прилегающих к стенкам каморы и канала ствола , мала по сравнению с диаметрами . Решение можно искать в одномерной постановке, т.е. предполагая , что параметры газа ( p , T , 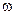 , U , c ) одинаковы в каком-то сечении и равны параметрам на оси канала ствола и каморы . Решение задачи Лагранжа , выполненное кандидатом физико-математических наук Зинченко Ю.К. в осемметричной постановке показало , что при
, U , c ) одинаковы в каком-то сечении и равны параметрам на оси канала ствола и каморы . Решение задачи Лагранжа , выполненное кандидатом физико-математических наук Зинченко Ю.К. в осемметричной постановке показало , что при 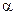 < 15 0 (угол конусности канала ствола) приводит к разнице результатов не более 10% в случаи решения этой задачи в одномерной постановке .
< 15 0 (угол конусности канала ствола) приводит к разнице результатов не более 10% в случаи решения этой задачи в одномерной постановке .
11.1 Основные уравнения одномерного движения газа и их решение.
Выделим в газе , находящемся в трубе , некоторый объем v . Сила , действующая на него равна - 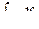 . В случае одномерного движения
. В случае одномерного движения
- 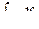 = -
= - 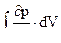
где p – давление ; f – площадь поверхности , ограничивающей объем ; dx – элемент длины ; 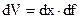 - элемент объема .
- элемент объема .
Уравнение движения будет иметь вид :
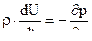
где 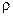 - плотность газа , U – скорость газа ,
- плотность газа , U – скорость газа , 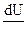 - ускорение газа .
- ускорение газа .
Производная 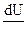 определяет не изменение скорости в данной неподвижной точке пространства , а изменение скорости данной частицы газа передвигающейся в пространстве , т.е. :
определяет не изменение скорости в данной неподвижной точке пространства , а изменение скорости данной частицы газа передвигающейся в пространстве , т.е. :
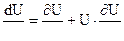
где 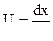 , t – время , x – координата .
, t – время , x – координата .
Таким образом приходим к уравнению движения в форме Эйлера :
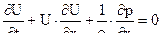
Рассмотрим закон сохранения массы газа , в нашем объеме она равна
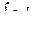 . Полная масса газа , вытекающего ( или втекающего ) через поверхность f за единицу времени будет равна:
. Полная масса газа , вытекающего ( или втекающего ) через поверхность f за единицу времени будет равна:
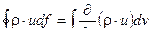
С другой стороны , уменьшение ( или увеличение ) массы газа в объеме за единицу времени будет - 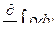 . Приравнивая оба выражения имеем :
. Приравнивая оба выражения имеем :
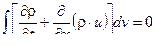
Это равенство справедливо для любого объема . Поэтому
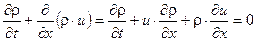 ( 11,2 )
( 11,2 )
Уравнение ( 11,2 ) называется уравнением неразрывности . Для изоэнтропического ( адиабатического ) течения газа уравнение энергии записывается в виде идеального газа :
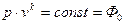 ( 11,3 )
( 11,3 )
Для реального газа , для которого справедливо уравнение состояния в виде
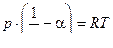 (пороховой газ).
(пороховой газ).
уравнение энергии будет иметь вид :
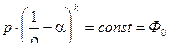 ( 11,4 )
( 11,4 )
где 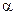 - коволюм единицы массы газа .
- коволюм единицы массы газа .
Для изоэнтропического течения преобразуем уравнение движения и уравнение неразрывности , выражая p и 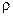 через теплосодержание i (энтальпию ) или скорость звука в газе с . Для этого воспользуемся следующими термодинамическими соотношениями :
через теплосодержание i (энтальпию ) или скорость звука в газе с . Для этого воспользуемся следующими термодинамическими соотношениями :
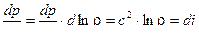
А случае изотропы :
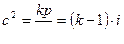
Для пороховых газов :
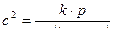 ( 11,5 )
( 11,5 )
Отметим: скорость звука реального газа выше скорости звука идеального газа ( 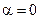 ).
).
Кроме с - скорости звука С.А. Бетехтеным был введен аналог скорости звука
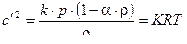
или 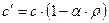 (11.6). Из соотношения ( 11,6 ) следует, что аналог скорости звука совпадает со скоростью звука в идеальный газе . Разрешая соотношения (11,5) , (11,4) , (11,6) относительно p и
(11.6). Из соотношения ( 11,6 ) следует, что аналог скорости звука совпадает со скоростью звука в идеальный газе . Разрешая соотношения (11,5) , (11,4) , (11,6) относительно p и 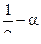 получим :
получим :
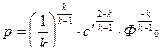 (11.7)
(11.7)
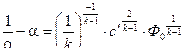
Если при помощи соотношений ( 11,6 ) и ( 11,7 ) исключить p и 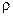 , то уравнения ( 11,1 ) и ( 11,2 ) будут иметь вид :
, то уравнения ( 11,1 ) и ( 11,2 ) будут иметь вид :
Для пороховых газов :
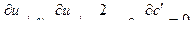 ( 11,8) - уравнение движения .
( 11,8) - уравнение движения .
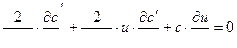 ( 11,9)- уравнение непрерывности .
( 11,9)- уравнение непрерывности .
Для идеального газа ( 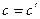 ) .
) .
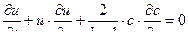 (11,10) и
(11,10) и
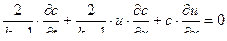 ( 11,11 )
( 11,11 )
Складывая или вычитая почленно уравнение (11,8) и (11,9) или (11.10) и (11.11)получим окончательно :
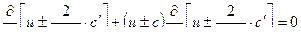 ( 11,12 ) для реального газа .
( 11,12 ) для реального газа .
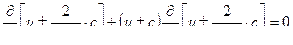 (11,13) для идеального газа .
(11,13) для идеального газа .
В таком виде уравнение ( 11,12 ) или ( 11,13 ) удобны для исследования . Очевидно , что заданные значения величины 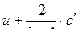 или
или 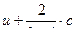 распространяются вправо со скоростью U+c , а заданное значение
распространяются вправо со скоростью U+c , а заданное значение
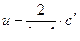 или
или 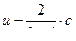 распространяется влево со скоростью U-c .
распространяется влево со скоростью U-c .
Таким образом любое произвольное движение газа можно разложить на два взаимодействующих друг с другом движения , на две волны , одна из которых распространяется вправо , другая влево .
Система уравнений ( 11,12 ) или ( 11,13 ) есть система уравнений в частных производных гиперболического тела . Методов решения их достаточно много. Мы остановимся на методе характеристик , который более наглядно дает физическую картину течения газа .
Решение задачи Лагранжа .
Задача Лагранжа в классическом ее понимании заключается в следующем.
В цилиндре , ограниченном слева неподвижной стенкой и безгранично продолженном вправо на расстоянии l0 от дна цилиндра находится поршень весом q . Площадь поперечного сечения цилиндра равна S0 . В пространстве между дном цилиндра и поршнем находится 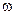 кг газа под давлением p0 с плотностью
кг газа под давлением p0 с плотностью 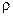 0 . Газ однороден и неподвижен . В момент t = 0 поршень получает возможность двигаться без сопротивления под действием давления газа . Движение газа является одномерным , влияние теплоотдачи не учитывается . Требуется определить возможное в этих условиях движение газа и движение поршня. Таким образом задача Лагранжа сводится к основной задачи внутренней баллистики в предположении о мгновенном сгорании заряда и отсутствии теплоотдачи сопротивления движению и других второстепенных работ , за исключением движения газа . Задача поставленная в 1790г. неоднократно привлекала к себе внимание многих ученых : Пиддек ( 1921г. ) , Госсо и Лиувиль(1922г. ) , Фок( 1935г. ) , Платрие ( 1936г. )-вот далеко не полный перечень ученых , посветивших свои работы решению этой задачи . Наиболее полно она решена С.А. Бетехтиным (1948г.) с учетом коволюма газа для каморы с уширением , с учетом теплоотдачи . Позднее она решалась Л.Л. Поповым , Зайченко Ю.И. ( в оссиметричной постановке ) , Никулиным О.А. в новых относительных переменных , Ушаковым В.М. , Комаровским А.В. и другими .
0 . Газ однороден и неподвижен . В момент t = 0 поршень получает возможность двигаться без сопротивления под действием давления газа . Движение газа является одномерным , влияние теплоотдачи не учитывается . Требуется определить возможное в этих условиях движение газа и движение поршня. Таким образом задача Лагранжа сводится к основной задачи внутренней баллистики в предположении о мгновенном сгорании заряда и отсутствии теплоотдачи сопротивления движению и других второстепенных работ , за исключением движения газа . Задача поставленная в 1790г. неоднократно привлекала к себе внимание многих ученых : Пиддек ( 1921г. ) , Госсо и Лиувиль(1922г. ) , Фок( 1935г. ) , Платрие ( 1936г. )-вот далеко не полный перечень ученых , посветивших свои работы решению этой задачи . Наиболее полно она решена С.А. Бетехтиным (1948г.) с учетом коволюма газа для каморы с уширением , с учетом теплоотдачи . Позднее она решалась Л.Л. Поповым , Зайченко Ю.И. ( в оссиметричной постановке ) , Никулиным О.А. в новых относительных переменных , Ушаковым В.М. , Комаровским А.В. и другими .
Решение задачи Лагранжа имеет большое практическое значение , т.к. позволяет установить основные закономерности движения газов и в более сложных случаях , каким является течение газопороховой смеси при выстреле из орудия .
С газодинамической точки зрения задача Лагранжа является задачей об одномерном неустановившемся движении газа при соответствующих начальных и граничных условиях . Если поместить начало координат у дна цилиндра и направить ось X в сторону движения поршня , то начальными условиями будут следующие : при t =0 0=<x<l0 , Р=Р0 ,  , U=0 , T=T0 .
, U=0 , T=T0 .
Граничные условия вытекают из того обстоятельства , что слои газа непосредственно прилегающие к дну цилиндра и к дну поршня не могут ни проникнуть через эту поверхность , ни отставать от них . По этому граничные условия будут формулироваться следующим образом :
X=0 , U=0
X=l+l0 , 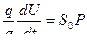 ( 11,14 )
( 11,14 )
где l - путь , пройденный поршнем к рассматриваемому моменту времени .
Допустим , что газ идеальный . Рассмотрим область движения в плоскости X,t . Слева она ограничена осью t , а справа - неизвестной еще нам кривой , изображающей закон движения поршня X=f(t) . Начальными условиями определены все искомые функции на отрезке 0 - l0 оси X . Известно , что f'(0)=0 , f''(0)>0 , f''(t)>0 , т.е. поршень начинает двигаться с нулевой скоростью , но с конечным ускорением , причем ускорение поршня остается положительным во время его движения . Поскольку слой газа , примыкающий к дну поршня не может ни оторваться , ни обогнать поршень в своем движении , будет всегда выполняться условие :
Ux=f(t)=f'(t)
где Ux=f(t) - скорость слоев газов , прилегающих к дну поршня . Таким образом скорость , а следовательно и остальные параметры переднего слоя будут непрерывно изменяться в результате движения поршня .
Расширение бесконечно тонкого газа будут вызывать расширение соседнего слоя газа , а это в свою очередь приведет к последовательному расширению все более и более удаленных слоев газов. Погазу будет распостраняться волна разряжения . Поскольку поршень движется с конечным ускорением , то за бесконечно малый промежуток времени скорость , а следовательно остальные параметры газа будут изменятся на бесконечно малую величину . Но ,как известно , бесконечно малые изменения параметров газа распостраняются по массе газа ,т.е. передаются от слоя к слою с вполне определенной скоростью , зависящей от давления и плотности газа и носящей название местной скорости звука в газе . Если при этом сами слои газа двигаются со скоростью "U" вправо , то бесконечно малые изменения параметров газа или элементарные возмущения будут перемещаться относительно неподвижных стенок трубы по закону
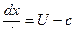 (11.15) , где С –скорость звука в газе (уравнение 11.15 нельзя записать в конечном виде т.к. "U" и "c" могут быть функциями "x" и"t" ).
(11.15) , где С –скорость звука в газе (уравнение 11.15 нельзя записать в конечном виде т.к. "U" и "c" могут быть функциями "x" и"t" ).
Допустим ,что нам удалось найти частное решение системы (11.13), т.е. отыскать такие две функции : 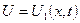 и
и 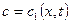 , которые удовлетворяют уравнениям (11.13) и граничному условию
, которые удовлетворяют уравнениям (11.13) и граничному условию 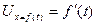 , имея это решение , мы можем построить в плоскости (x,t) систему линий
, имея это решение , мы можем построить в плоскости (x,t) систему линий
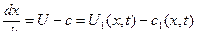 , которые называются характеристиками (рис… фиг.2).
, которые называются характеристиками (рис… фиг.2).
В условиях задачи Лагранжа , линии будут прямыми , идущими расходящимися пучками , т.е. на одно элементарное возмущение не будет в процессе своего перемещения обгонять предыдущее ,т.к. скорость звука падает при расширении . А так как каждое последующее элементарное возмущение распостраняется по газу , все более и более разряженному , воздействием предыдущих возмущений , то отсюда и следует , что одно последующее возмущение не сможет догнать предыдущее . Система значений U=0 и с=с0 нетрудно убедится , также будет одним из частных решений системы U=U1(x,t) и c=c1(x,t) будут справедливы лишь выше линии ОА . Таким образом вдоль линии ОА происходит переход от одного частного решения системы к другому .
Как было показано выше вдоль характеристик выполняются соотношения 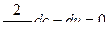 , аналогично вдоль характеристики , идущей вправо
, аналогично вдоль характеристики , идущей вправо 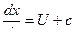 будет выполнятся соотношение
будет выполнятся соотношение 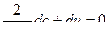 или окончательно можно записать :
или окончательно можно записать : 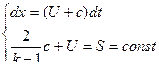 (11.16)
(11.16)
( характеристики I семейства
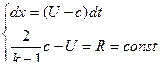 (11.17)
(11.17)
( характеристики II семейства
S и R называются инвариантами Римана .
Уравнения (11.16) и (11.17) имеют вполне определенный физический смысл. Уравнения характеристик в плоскости x, t как следует выше описывают законы перемещения элементарных возмущений . Уравнения же характеристик в плоскости искомых функций определяют связь между изменениями скорости течения "U" и местной скорости звука –"с" , которая должна выполнятся при перемещении данного элементарного возмущения .
Значения "U" и "с" в любой точке области движения можно выразить через S и R в этой точке , т.е. через значения постоянных интегрирующих вдоль характеристик , противоположных семейств , проходящих через данную точку 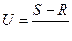 ,
, 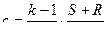 (11.18)
(11.18)
Поскольку S или R сохраняют постоянное значение вдоль данной характеристики соответственного семейства , но могут принимать различные значения вдоль различных характеристик этого семейства , то вообще говоря возможно следующие три случая :
1. В некоторой части плоскости (x, t) S имеет на всех характеристиках I семейства одно и то же значение S=Idcm, а R=Idm. одно и то же значение на всех характеристиках II семейства в этой же части плоскости ,т.е. во всех точках плоскости U=const и c=const , т.е. поток газа будет в этой части плоскости однородным . Если при этом S=R,то U=0 ,а с=с0 рассматриваемая область будет областью покоя ( рис…)
2. Постоянные интегрирования одного из семейств ( предположим ,что I семейства ) сохраняет постоянное значение в некоторой области (S=Idm.) постоянные же интегрирования другого семейства (II семейства ) R меняется от характеристики к характеристике. Поэтому в пределах рассматриваемой области вдоль каждой характеристики II семейства в плоскости x, t скорость течения "U" и местная скорость звука будут сохранять постоянные значения (S=Idm. R=const вдоль этой характеристики ) I семейства , то сами характеристики II семейства будут прямыми линиями. Течения такого рода носят названия волн одного направления (рис..) .Так как вдоль линии ОА все характеристики I семейства имеют одно и то же значение S=Idm, то в области волны одного направления характеристики II семейства будут прямыми линиями , а характеристики I семейства, где в каждой точке только S=const ,а R –меняется ,эти характеристики I семейства будут кривыми линиями . Характеристики I семейства –кривая АВ будет отделять область волны одного направления от области , где S, R меняться от характеристики к характеристики ( область общего случая неустановившегося движения в газе ).
3. Третий случай , когда в пределах рассматриваемой области оказываются переменными как S так и R это является наиболее общим случаем неустановившегося движения газа . Для этого случая нельзя установить каких-либо иных закономерностей , кроме тех, которые заложены в самих уравнениях характеристик.
В области волны одного направления параметры газа и скорость течения , а также закон движения поршня находятся по аналитическим зависимостям . В общим случае , задачи решаются численно . Если ОА разбить на 256 отрезков , то значения 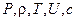 находятся с точностью до 0,1% в области волны одного направления , эту точность можно перенести и в общий случай . Как правило , чтобы уменьшить количество вариантов задача Лагранжа решается в относительных переменных . Обычно за отнсительные переменные принимаются :
находятся с точностью до 0,1% в области волны одного направления , эту точность можно перенести и в общий случай . Как правило , чтобы уменьшить количество вариантов задача Лагранжа решается в относительных переменных . Обычно за отнсительные переменные принимаются :
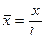 ,
, 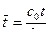 ,
, 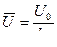 ,
, 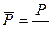 ,
, 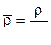 ,
, 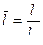 ,
, 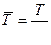 (11.19)
(11.19)
Такие относительные переменные неудобны при оценке влияния коволюма газа , ускорения поршня длины ствола , уширения каморы .
В частности ,в этих относительных переменных решена задача Лагранжа ,С.А. Бетехтиным ,Н.Н. Поповым и другими . Из результатов решения трудно выявить волновую картину процесса расширения газа .
О.А. Никулиным предложены новые относительные переменные , которые свободны от перечисленных выше недостатков .
За единицу измерения параметров принимаются : 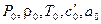 , где
, где 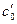 - аналог скорости звука в газе , равный
- аналог скорости звука в газе , равный
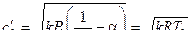 (11.20)
(11.20)
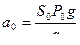 - начальное ускорение поршня (11.21)
- начальное ускорение поршня (11.21)
S0 –площадь сечения канала ствола
q –вес снаряда
Р0 –начальное (максимальное давление газа)
Т0 –начальная температура(max)
R –газовая постоянная
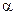 - ковалюм единицы массы газа
- ковалюм единицы массы газа
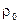 -начальная плотность газа (max)
-начальная плотность газа (max)
K –показатель адиабаты
Тогда 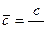 ,
, 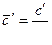 ,
, 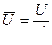 ,
, 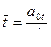 ,
, 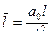 ,
, 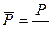 ,
, 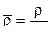 ,
, 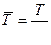 (11.22)
(11.22)
В области волны одного направления относительные переменные определяются по следующим формулам ( в зависимости от 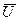 )
)
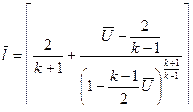 (11.23)
(11.23)
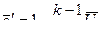 (11.24)
(11.24)
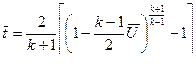 (11.25)
(11.25)
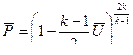 (11.26)
(11.26)
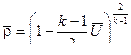 (11.27)
(11.27)
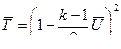 (11.28)
(11.28) 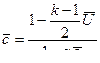 (11.29)
(11.29)
Уравнение справедливо до момента т. В ,когда отраженная от дна канала ствола волна догонит снаряд
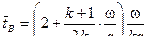 (11.30)
(11.30)
Откуда оптимальный относительный вес газа
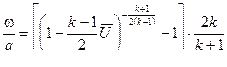 (11.31) , т.е. когда отраженная от дна каморы волна догонит снаряд у дульного среза .
(11.31) , т.е. когда отраженная от дна каморы волна догонит снаряд у дульного среза .
Из выражения (11.20-11.31) следует ,что скорость снаряда 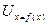 и параметры газа
и параметры газа 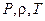 , а также оптимальное значение
, а также оптимальное значение 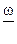 при одних и тех же значениях
при одних и тех же значениях 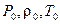 и длине ствола S0 не зависят от ковалюма газов влияет только на объём каморы , или длину каморы при S0=const увеличивая её на величину
и длине ствола S0 не зависят от ковалюма газов влияет только на объём каморы , или длину каморы при S0=const увеличивая её на величину 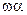 . Численные расчеты показывают справедливость такого вывода и в более общем случае .
. Численные расчеты показывают справедливость такого вывода и в более общем случае .
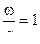 газ водород
газ водород
Таблица 25
|
|
| ||||
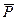
| 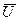
| 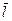
| 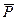
| 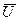
| 
|
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0,7881 | 0,1671 | 0,00157 | 0,7882 | 0,1671 | 0,0016 |
| 0,6351 | 0,3137 | 0,00650 | 0,6352 | 0,3137 | 0,0065 |
| 0,5242 | 0,4440 | 0,0150 | 0,5214 | 0,4440 | 0,0152 |
| 0,4344 | 0,5614 | 0,0276 | 0,4346 | 0,5614 | 0,0275 |
| 0,3668 | 0,6673 | 0,0437 | 0,3669 | 0,6669 | 0,0437 |
| 0,3134 | 0,7638 | 0,0641 | 0,3135 | 0,7634 | 0,0640 |
| 0,2704 | 0,8519 | 0,0885 | 0,3705 | 0,8519 | 0,0885 |
| 0,2553 | 0,9336 | 0,1172 | 0,2354 | 0,9332 | 0,1172 |
| 0,0881 | 1,1314 | 0,2606 | 0,0883 | 1,1311 | 0,2602 |
| 0,0361 | 1,262 | 0,5385 | 0,0361 | 1,2613 | 0,5373 |
| 0,01558 | 1,354 | 1,0472 | 0,0155 | 1,3533 | 1,0439 |
| 0,00689* | 1,421* | 1,9520* | 0,0069* | 1,4205* | 1,9456* |
| 0,003116 | 1,472 | 3,548 | 0,0031 | 1,4718 | 3,5328 |
| 0,001427 | 1,512 | 6,3531 | 0,0014 | 1,5113 | 6,3222 |
В таблице отмечены изменения давления на снаряд , относительная скорость снаряда и относительный путь снаряда для идеального водорода ( 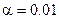 ) и реального водорода (
) и реального водорода ( 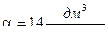 ). Из таблицы видно ,что коволюм не влияет на эти характеристики и так как расчеты проводились в абсолютных значениях величин , а обработка в новых относительных переменных , то видно ,что точность расчета выше чем 0,1% (при сравнении с аналитическими формулами (11.20)-(11.31)).
). Из таблицы видно ,что коволюм не влияет на эти характеристики и так как расчеты проводились в абсолютных значениях величин , а обработка в новых относительных переменных , то видно ,что точность расчета выше чем 0,1% (при сравнении с аналитическими формулами (11.20)-(11.31)).
На рис…показано изменение относительного давления от скорости снаряда , а на рис….. изменение относительной скорости от относительного пути снаряда . Из рис. 1 и 2 видно ,что огибающие кривых соответствуют случаю когда 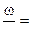 ∞ , точками 0.5;1.0;1.5;2.0;2.5;3.0;3.5;4.0;5.0;6.0;7.0 соответствует значению
∞ , точками 0.5;1.0;1.5;2.0;2.5;3.0;3.5;4.0;5.0;6.0;7.0 соответствует значению 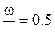 ,
, 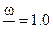 и т.д. и они показывают :
и т.д. и они показывают :
1. при заданной относительной длине ствола 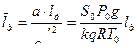 , соответствует максимальной относительной скорости снаряда и оптимальное значение веса газа , т.е.
, соответствует максимальной относительной скорости снаряда и оптимальное значение веса газа , т.е. 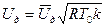 и
и 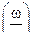
2. Если мы увеличим количество газа 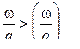 , то скорость снаряда ни найоту не увеличивается ,т.е. дополнительное количество газа просто не участвует в передачи энергии снаряду т.к. дополнительного слоя волна разряжения идущая от дна снаряда не успела дойти , а снаряд вылетел из ствола .
, то скорость снаряда ни найоту не увеличивается ,т.е. дополнительное количество газа просто не участвует в передачи энергии снаряду т.к. дополнительного слоя волна разряжения идущая от дна снаряда не успела дойти , а снаряд вылетел из ствола .
Если мы уменьшим количество газа т.е. 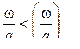 , то получим резкое падение скорости снаряда при заданной длине ствола
, то получим резкое падение скорости снаряда при заданной длине ствола
Например, при  ,
, 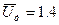 ,
, 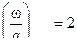 ,
, 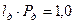 ,
, 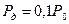 ,
,
при 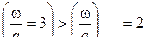 и
и  ,
, 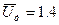 ,
, 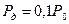 , то есть ни дульная скорость снаряда, ни дульное давление не увеличивалось.
, то есть ни дульная скорость снаряда, ни дульное давление не увеличивалось.
Увеличилась только длина каморы в 1,5 раза . Этот вывод не был бы сделан если бы не делали пересчет при использовании прежних относительных переменных 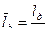 , при
, при 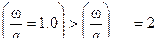 при
при  , которое не зависит от
, которое не зависит от  (это важно ,при обычных относительных переменных
(это важно ,при обычных относительных переменных 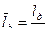 увеличилась бы в 2 раза ) дульная скорость
увеличилась бы в 2 раза ) дульная скорость 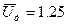 ,
, 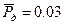 .
.
На рис. 3 приведены оптимальные значения  для разных газов , принимая
для разных газов , принимая
показатель адиабаты для гелия 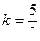 , для водорода
, для водорода 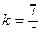 и пороховых газов
и пороховых газов  . Уравнения (11.23),(11.26),(11.31)примут вид :
. Уравнения (11.23),(11.26),(11.31)примут вид :
для гелия 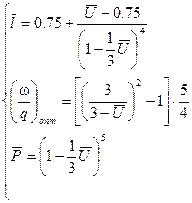
для водорода 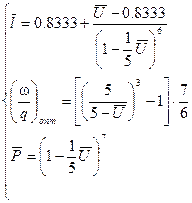
для пороховых газов 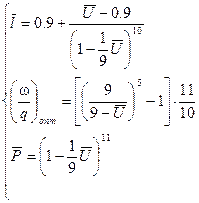
Результаты расчетов представлены в таблице 26
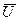
|
|
|
| ||||||
| 5/3 | 7/5 | 11/9 | 5/3 | 7/5 | 11/9 | 5/3 | 7/5 | 11/9 | |
| 0,5 | 0,2316 | 0,206 | 0,191 | 0,550 | 0,434 | 0,364 | 0,4996 | 0,4997 | 0,4998 |
| 1,0 | 2,016 | 1,469 | 1,225 | 1,56 | 1,11 | 0,902 | 0,9949 | 0,9956 | 0,9987 |
| 1,5 | 12,75 | 6,50 | 4,615 | 3,75 | 2,24 | 1,64 | 1,484 | 1,476 | 1,484 |
| 2,0 | 102 | 25,8 | 14,5 | 10 | 4,24 | 2,76 | 1,884 | 1,93 | 1,95 |
| 2,5 | 2269 | 107,5 | 42,34 | 43,8 | 8,17 | 4,5 | 2,19 | 2,333 | 2,386 |
| 3,0 | - | 529,8 | 122,0 | - | 17,0 | 7,25 | - | 2,67 | 2,78 |
| 3,5 | 358,9 | 11,8 | 3,075 | ||||||
| 4,0 | 1108 | 19,7 | 3,42 | ||||||
В таблице приведены результаты скорости снаряда 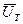 в случае использования классического метода расчета –" термодинамического " расширения газа .
в случае использования классического метода расчета –" термодинамического " расширения газа .
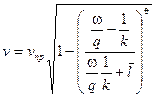 ,где
,где 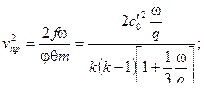
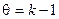 или окончательно
или окончательно
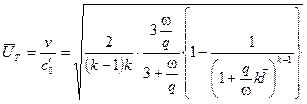 (11.32)
(11.32)
при одинаковых значениях  и
и  .
.
Из таблицы в частности видно ,что при дульных скоростях снаряда для пороховых газов 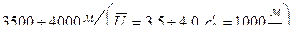 .
.
Термодинамическое расширение даёт дульную скорость на 500-600 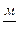 ниже , а при скорости 3,5-3,8
ниже , а при скорости 3,5-3,8 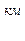 реально получены на установках ППН для легких снарядов (
реально получены на установках ППН для легких снарядов ( 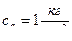 ) .Из соотношения (11.32) ,найдем оптимальное значение
) .Из соотношения (11.32) ,найдем оптимальное значение 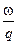 , которое дает максимальное значение скорости при заданной длине ствола
, которое дает максимальное значение скорости при заданной длине ствола 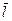 .
.
Дифференцируя и приравнивая 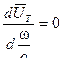 , получим соотношение :
, получим соотношение :
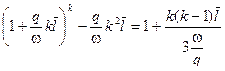 (11.33)
(11.33)
Разрешая это уравнение , находим 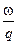 .
.
Например . Для пороховых газов 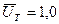 получим вместо
получим вместо 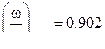 значение
значение 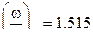 при этом
при этом 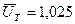 , т.е. 2.5% больше , что не может быть т.к. в передаче энергии снаряду участвует лишь
, т.е. 2.5% больше , что не может быть т.к. в передаче энергии снаряду участвует лишь 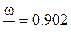 или пусть
или пусть 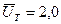 получим вместо
получим вместо 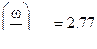 значение
значение 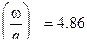 при этом
при этом 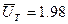 вместо
вместо 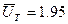 , однако количество газа участвующая в передаче энергии снаряду равно
, однако количество газа участвующая в передаче энергии снаряду равно 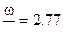 . Остальное количество газа лишнее .
. Остальное количество газа лишнее .
11.3 Влияние уширения каморы.
Из графиков рис. 1 и 2 ясно , чтобы увеличить скорость снаряда при заданной природе газа , максимальном давлении и заданной длине ствола , необходимо длину каморы оставить без изменения , но увеличить поперечное сечение каморы ,т.е. x>1 , тогда большее количество газа будет участвовать в передаче энергии снаряду .
Результаты расчетов при больших значениях 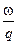 и резком переходе из газовой каморы l ствол приведены на рис.3 .
и резком переходе из газовой каморы l ствол приведены на рис.3 .
Приближенно оценить увеличение скорости снаряда за счет уширения каморы можно по выведенным О.А. Никулиным формулам
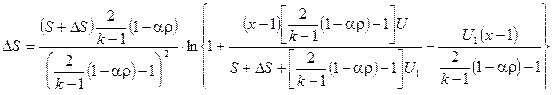 (11.34)
(11.34)
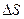 увеличение инвариантно S
увеличение инвариантно S
где 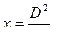 "U1", и "U" скорости газа на входе и выходе из соединительного конуса между каморой стволом .
"U1", и "U" скорости газа на входе и выходе из соединительного конуса между каморой стволом .
Формула (11.34) выведена при предположении ,что 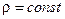 в переходном конусе .
в переходном конусе .
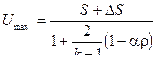 (11.35)
(11.35)
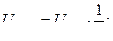
Подставляя (11.35) в уравнении (11.34) окончательно получим
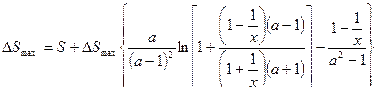 (11.36)
(11.36)
где 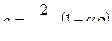
Для бесконечного уширения каморы x=∞ получим
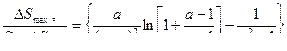 (11.37)
(11.37)
Результаты 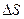 полученные для водорода и гелия при
полученные для водорода и гелия при 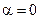 и разных значениях уширения каморы приведены в таблице 27
и разных значениях уширения каморы приведены в таблице 27
Таблица 27
|
| водород | гелий | ||
| приближенное | точное | приближенное | точное | |
| 4 | 0,388 | 0,302 | 0,347 | 0,288 |
| 16 | 0,587 | 0,402 | 0,570 | 0,388 |
| ∞ | 0,605 | 0,645 | ||
Точное решение полученное при решении задачи Лагранжа с уширением каморы 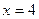 и 16 при нахождении точного решения радиуса переходного конуса имеем вид
и 16 при нахождении точного решения радиуса переходного конуса имеем вид 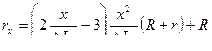 (11.38)
(11.38)
где 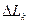 -высота переходного конуса R и r радиусы каморы и ствола , соответственно . В таблице 28 приведены результаты расчетов для реального водорода (
-высота переходного конуса R и r радиусы каморы и ствола , соответственно . В таблице 28 приведены результаты расчетов для реального водорода ( 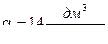 ) с уширением каморы x=16 и разных значениях
) с уширением каморы x=16 и разных значениях 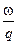
Таблица 28
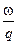
| 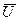
| 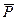
| 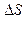
| 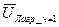
| 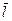
|
| 1 | 0,1921 | 0,9239 | 0,1358 | 0,0563 | 0,019 |
| 2 | 0,3757 | 0,8232 | 0,238 | 0,1370 | 0,081 |
| 3 | 0,5469 | 0,7180 | 0,260 | 0,2871 | 0,187 |
| 4 | 0,7046 | 0,6212 | 0,3190 | 0,3854 | 0,346 |
| 10 | 1,1032 | 0,3854 | 0,4684 | 0,6663 | 1,206 |
| 20 | 1,6860 | 0,1668 | 0,5574 | 1,1286 | 5,03 |
| 32 | 2,1028 | 0,0800 | 0,5889 | 1,5139 | 13,684 |
| 40 | 2,207 | 0,0544 | 0,595 | 1,702 | 21,80 |
| 64 | 73,065 | 0,0074 | 0,5458 | 2,519 | 144,17 |
Как видно из таблицы в случае реального водорода (с учетом ковалюма ) значение 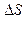 приближается к 0,595 т.е. к вычисленной по приближенной формуле 0,587 для идеального водорода . Таим образом реально получить приращение 500-600м/с при одинаковых и максимальных давлениях используя уширение каморы x=16 или
приближается к 0,595 т.е. к вычисленной по приближенной формуле 0,587 для идеального водорода . Таим образом реально получить приращение 500-600м/с при одинаковых и максимальных давлениях используя уширение каморы x=16 или 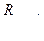 .
.
Этот вывод важен при проектировании пороховых и легкогазовых установок и повышения начальной скорости снаряда из боевого орудия , для получения скорости свыше 2000 м/с.
11.4 Условия постоянного давления на снаряд по всей длине ствола.
При горении пороха рассмотрим характеристику I семейства в области волны одного направления  откуда
откуда
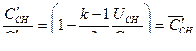 т.к. имеется зависимость
т.к. имеется зависимость  получим
получим
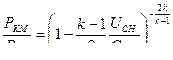 или
или
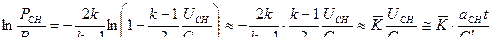 (11.39)
(11.39)
где используется соотношение 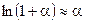 при малых значениях
при малых значениях 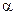 .В случае пороховых газов
.В случае пороховых газов 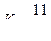 ,
, 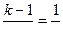
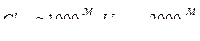
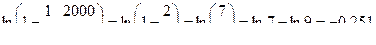 ,
, 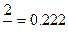 т.е. ошибка равна
т.е. ошибка равна 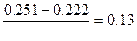 т.е. ошибка составляет 13% в сторону занижения .(
т.е. ошибка составляет 13% в сторону занижения .( 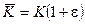 , где
, где 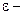 относительная ошибка ). Рассмотрим пороховую камору большого объёма , когда количеством газа можно пренебречь , тогда
относительная ошибка ). Рассмотрим пороховую камору большого объёма , когда количеством газа можно пренебречь , тогда
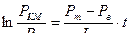 (11.40)
(11.40)
при 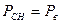 получим
получим 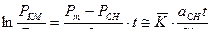 т.к.
т.к. 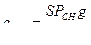 , то окончательно
, то окончательно 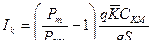 (11.41), т.е. зная максимальное давление в каморе и давление на снаряд, которое постоянно по стволу и
(11.41), т.е. зная максимальное давление в каморе и давление на снаряд, которое постоянно по стволу и  , легко получить марку пороха и все остальные характеристики .
, легко получить марку пороха и все остальные характеристики .
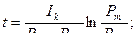
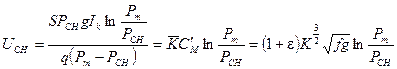 ,принимая
,принимая
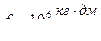 и К=11/9 получим
и К=11/9 получим 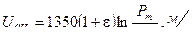 ;
; 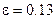 при
при 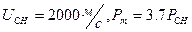 .
.
В качестве воспламенителя можно использовать любой быстро горящий порох , который выводит на заданный уровень давления на дно снаряда ,т.е. порох должен быть комбинированный.
12.Пороховые и легко газовые установки.
Пороховые и легко газовые установки нашли широкое применение при гиперзвуковых исследованиях .
Пороховые установки рис. 55 как и орудие имеет ствол , пороховую камору и затвор . В пороховых установках ППН , созданных под руководством О.А. Никулина : на ствол, навинчивался пороховой стакан , представляющий собой толстостенную болванку со сплошным дном . В болванке имеется камора с уширением x=3,6 переходящая в цилиндр диаметром равным диаметру канала ствола . В ствол помещалось метаемое тело в поддоне. Иногда между стволом и пороховым стаканом помещалась мембрана со специальной насечкой для увеличения давления форсирования снаряда . В дне болванки имелось отверстие , через которое вставлялся инициирующее устройство в камору . Ствол со стаканом размещался на легкой раме . При выстреле установка отскакивала назад . Калибры ствола 23;34;50. Длина ствола 70-80клб. Давление в каморе 10000-15000кг/см2. Скорости ,полученные на установках со снарядом Сq=1,0-2,0кг/дм3 были 3000-2600 м/с соответственно.
На установках использовались штатные пороха. Были проведены специальные стрельбы по выяснению влияния различных фактов влияющих на баллистику выстрела , в частности применение различных добавок и основному заряду , использование комбинированных зарядов и желеобразных топлив и т.д. Проектирование установок базировалось на результатах решения задачи Лагранжа в новых относительных переменных ,предложенных О.А. Никулиным . В дальнейшем установки ППН были модернизированы с увеличением объёма каморы , и её уширения до x=8-9 при этом достигнуты скорости  на тех же калибрах . При решении ОЗВБ использовался газодинамический метод , разработанный профессором В.М. Ушаковом.
на тех же калибрах . При решении ОЗВБ использовался газодинамический метод , разработанный профессором В.М. Ушаковом.
На установках ППН проведены несколько десятков тысяч опытов . Типичный характер изменения давления от пройденного пути снарядом представлены на рис 56 легкогазовые установки.
Как известно , максимальная возможная скорость неустановившегося течения 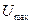 :
: 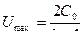 , которая прямо пропорционально скорости звука в газе . При одинаковой температуре газа наибольшей энергией будут обладать атомарный водород , гелий , так называемые легкие газы . Скорость звука молекулярного водорода при комнатной температуре примерно 1300м/с , выше скорости звука пороховых газов (
, которая прямо пропорционально скорости звука в газе . При одинаковой температуре газа наибольшей энергией будут обладать атомарный водород , гелий , так называемые легкие газы . Скорость звука молекулярного водорода при комнатной температуре примерно 1300м/с , выше скорости звука пороховых газов (  1000м/с) .Если нагреть легкие газы до температуры 2000-2500К , то скорость звука 3000-4000м/с, а следовательно и максимальная скорость снаряда будет значительно выше , чем она достигнута на пороховых установках . Нагреть водород или гелий можно различными способами : электрическим разрядом , ударной волной, стехиометрической смесью кислорода и водорода (геливопаровая пушка) и движущимся поршнем , который сжимает легкий газ и в процессе сжатия нагревает его до нужной температуры . Поршневые легко газовые установки оказались наиболее перспективные и на них достигнуты скорости до 12 км/с ,скорости 7-8км/с являются рабочими скоростями ЛГУ , где используется деформируемый поршень . На рис.57 показано схематически ЛГУ с легким поршнем .
1000м/с) .Если нагреть легкие газы до температуры 2000-2500К , то скорость звука 3000-4000м/с, а следовательно и максимальная скорость снаряда будет значительно выше , чем она достигнута на пороховых установках . Нагреть водород или гелий можно различными способами : электрическим разрядом , ударной волной, стехиометрической смесью кислорода и водорода (геливопаровая пушка) и движущимся поршнем , который сжимает легкий газ и в процессе сжатия нагревает его до нужной температуры . Поршневые легко газовые установки оказались наиболее перспективные и на них достигнуты скорости до 12 км/с ,скорости 7-8км/с являются рабочими скоростями ЛГУ , где используется деформируемый поршень . На рис.57 показано схематически ЛГУ с легким поршнем .
ЛГУ состоит из пороховой каморы поз.1 , в которой размещен пороховой заряд и газовой каморы поз.4, в которую накачивается легкий газ ( водород или гелий )при комнатной температуре до давления 5-30кг/см2 . Пороховая камора отделена от газовой поршнем , выполненного из легко деформируемого материала (полиэтилена ). Газовая камера соединяется со стволом (поз.8) с помощью конического переходника (поз.5) , выдерживающей высокие давления газа (8000-15000кг/см2) . В ствол вставляется снаряд (поз.9) , состоящей из метаемого тела , которое помещается в поддоне из легкого прочного материала , так что относительный вес снаряда Сq=1-3кг/дм3. Метаемое тело отделено от легкого газа диафрагмой (поз.10) , которая раскрывается при определенном заданном давлении ( давления форсирования –Рф). Установка работает следующим образом : при подаче электрического импульса на инициирующее устройства, устройство срабатывает и воспламеняет пороховой заряд . При достижении давления форсирования , которое больше или равно начальному давлению водорода , поршень начинает двигаться по газовой камере . По мере сгорания порохового заряда поршень двигаясь с большой скоростью сжимает легкий газ и нагревает его : создаются определенные условия по давлению и температуре . При достижении заданного давления легкого газа –Рф диафрагма разрывается и снаряд – метаемая сборка под действием легкого газа разгоняется по вакуумированому стволу до заданной скорости . Такая легко газовая установка называется двух ступенчатой ЛГУ с "легким " поршнем . В первую ступень входит пороховая камера и поршень. Выстрел из первой ступени подобен выстрелу из обычного орудия с противодавлению снаряду . Решение задачи внутренней баллистики первой ступени и методы идентичны ОЗВБ орудия. Здесь могут быть использованы как газодинамический , так " термодинамический " методы решения . Разделение поршней на "тяжелый " и "легкий" связано с достижением поршнем скорости больше или меньше скорости звука . При малых скоростях поршня ("тяжелый" поршень ) ударной волны не образуется в легком газе и метод характеристик , изложенный выше как правило используется при решении ОЗВБ второй ступени . В случае использования "легкого " поршня газодинамический подход к решению ОЗВБ второй ступени обязательные методы "сквозного " счета , где ударная волна "размазывается " за счет введения "искусственной " вязкости газа .
Типичная картина изменения давления в пороховой и газовой камерах представлены на рис…..
Исследование внутренней баллистики ЛГУ усложняется не только за счет увеличения количества параметров , от которых зависит процесс выстрела , но и конструктивным оформлением поршня, диафрагмы , метаемой сборки , наличие конического переходника , в котором происходит торможение поршня в целом при одновременном ускорении его переднего торца за счет "гидроэффекта " . Приборы и аппаратура используемая при внутри баллистических исследованиях базируется на последних достижениях науки и техники в области быстропротекающих процессов и главное –результаты исследований , достижения в ЛГУ вполне могут быть перенесены на баллистику орудия . В этом смысле исследование в ЛГУ –это "форпост" в баллистике орудия. В доказательство этого вывода являются докторские диссертации Л.В. Комаровского , Ю.П. Хоменко , В.М. Ушакова , В.В. Жаровцева и др.
Список используемых источников
1. Благонравов А.А. Основы проектирования автоматического оружия
2. "Баллистические установки и их применение в экспериментальных исследованиях" под. ред. Златина Н.А. и Мишина О.А. издательство "Наука" , Москва 1974г.
3. Бетехтин С.А. , Виницкий М.А. , Горохов М.С. и др. "Газодинамические основы внутренней баллистики" . Издательство оборонной промышленности , Москва – 1957г.-384с.
4. "Бог войны" . Сборник статей . Автор-составитель полковник Латухин А.И. Издательство "Молодая гвардия" , Москва , 1879. , 256с.
5. Профессор Горохов М.С. "Внутренняя баллистика" . Отчет СФТИ при ТГУ им. В.В. Куйбышева , г. Томск , 1950г., 273с.
6. Корнер
7. Иванников Л.С. и Никулин О.А.
"Эксперементально-теоретическое определение силы сопротивления для 37ми мм. снаряда при врезании в нарезы канала ствола орудия" . Дипломная работа , ТГУ , г. Томск , 1957г. –96с.
8. Никулин О.А. "Приложение" к диссертации К.Т.Н. по спецтеме ( инв. №4034 ) , г. Бийск , 1968-40с.
9. Профессор Орлов Б.В. и Мазинг Г.Ю.
"Термодинамические и баллистические основы проектирования ракетных двигателей на твердом топливе" . Второе издание , переработанное и дополненное . Издательство "Машиностроение" , Москва ,1968г. –536с.
10. "Проектирование ракетных и ствольных систем" под редакцией д.т.н. проф. Орлова Б.В. Издательство "Машиностроение" , Москва , 1974г.-828с.
11. Академик Зельдович Я.Б. , Лейпунский О.И. , Либрович В.Б.
"Теория нестационарного горения пороха" , М. "Наука" 1975г.-131с.
12. Христенко Ю.Ф. и Жалнин Е.В.
"Монометрическая бомба" . Заявка на изобретение №2000118367
приоритет от 10.7.2000г.
13. Христенко Ю.Ф. "Экспериментальные методы исследования нестационарных эффектов при горении заряда зерненного пороха // исследование по баллистики и смежным вопросам механики" Вып.3 , Томск ,
издательство ТГУ , 1999г. , стр. 38-39 .
14. Христенко Ю.Ф. "Экспериментальные методы исследования закономерностей горения зерненных порохов в широком диапазоне изменения плотностей заряжания" . Доклады региональных конференций
Волж.Р.Ц. РАРАН "Современные методы проектирования и обработки ракетно-артиллерийского вооружения" , г. Саратов , издательство
РФЯ.Ц. - ... 2000г. с341-354 .
15. Проф. Серебряков М.Е. "Внутренняя баллистика" – М. , Оборонгиз , 1949г. , 458с.
16. Проф. Серебряков М.Е. "Внутренняя баллистика ствольных систем и пороховых ракет" 3-е издание , дополненное и переработанное ГНТИ оборонгиз , Москва 1962г. – 704с.
17. Тюлина И.А. "Жозеф Луи Лагранж" издательство "Наука" , Москва 1977г. 224с.
18. ЭРР "Артиллерия в прошлом , настоящем и будущем" . Военное издательство НК Обороны Союза ССР , Москва 1941г. – 348с.
19. Фундаментальные и прикладные проблемы современной механики (доклады 2-ой всероссийской научной конференции) . г. Томск, 6-8 июня 2000 г.
Дата: 2019-07-24, просмотров: 483.