Закон сохранения энергии устанавливает, что энергия не создается и не уничтожается и что одна форма энергии может переходить в другую. Превращение энергии из одного вида в другой происходит в строго определенных соотношениях, которые постоянны. Например, тепловвая энергия может превращаться в механическую (в виде совершения работы) и наоборот, работу в теплоту, причем, определенное количество тепла эквивалентно определенному количеству работы. Если тепло измеряется в тепловых единицах (ккал), а работа – в механических (кгдм), то константа указанного отношения Е ( 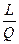 = Е или L = E Q) носит название механического эквивалента тепла Е = 4264,5 ≈ 4270 кгдм/ккал.

Величина, обратная Е называется тепловым эквивалентом работы.

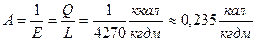
              Первый закон термодинамики

Первый закон термодинамики гласит: при подводе к газу тепла одна часть его расходуется на увеличение внутренней энергии газа, а другая на совершение газом внешней работы, что выражается следующей формулой:

                               Q = Δu + Aℓ                                              (2.19.)

Или для равновесных процессов

                                           dq = du + Apdw

Применительно к идеальным газам

                               dq = СwdT + Apdw                                  (2.20.)

Для изобарного процесса dq = СрdT. Подставим это выражение в уравнение (2.20.) и используя уравнение состояния для идеального газа, окончательно получим формулу Майера

                                 Ср = Сw + AR

              Энтальпия газа

Формулу (2.20.) можно представить в виде

                   dq = du + Apdw = du + Ad(pw) – Awdp = di – Awdp

где: i = u + Apw – энтальпия газа.

Энтальпия газа, как и внутренняя энергия не зависит от характера процесса.

Для изобарного процесса dq = du или СрdT = du                   (2.21)

Для адиабатического процесса – процесса без подвода или отвода тепла (dq = 0) имеем dq = СwdT + Apdw = 0.

Из уравнения состояния 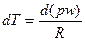, подставив в предыдущее уравнение получим 

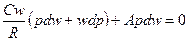
Используя формулу Майера окончательно получим 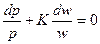 или

                               р·w^к = const                                                           (2.22.)

В случае газа Дюпре

                               р·(w – в)^к = const                                                  (2.23.)

              Политропический процесс

Реальные термодинамические процессы настолько сложны, и иногда практически невозможно составить уравнение, чтобы учесть, например, диссоциации, рекомбинацию молекул, теплоотдачу и т.д. Поэтому в расчетах такие процессы заменяют фиктивным или политропическим процессом, который имеет вид р·wⁿ = const

где n – показатель политропы. В зависимости от показателя политропы мы можем получить:

адиабатический процесс, когда n = к;

изобарный процесс, когда n = 0;

изохорный процесс, когда n = ± ∞;

изотермический процесс, когда n = 1;

Таким образом, реальный процесс с достаточной точностью можно аппроксимировать политропическим процессом, меняя значения n по участкам, на которые разбит реальный процесс. Политропному процессу, как и всякому из перечисленных выше процессу соответствует своя теплоемкость C, которая имеет вид

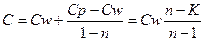                                                           (2.24.)