Определение координат центра тяжести.
Цель: Изучить пространственную систему сил и методы определения координат центров тяжести.
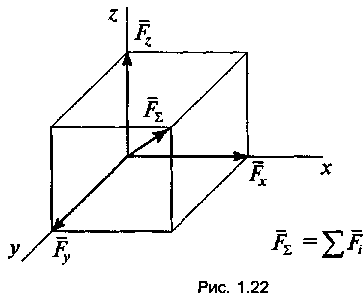 Пространственной системой сходящихся сил называется система сил, линии действия которых не лежат в одной плоскости, но пересекаются в одной точке. Равнодействующая такой системы сил изображается диагональю прямоугольного параллелепипеда, построенного на этих силах как на сторонах (рис. 1.22).
Пространственной системой сходящихся сил называется система сил, линии действия которых не лежат в одной плоскости, но пересекаются в одной точке. Равнодействующая такой системы сил изображается диагональю прямоугольного параллелепипеда, построенного на этих силах как на сторонах (рис. 1.22).
Условие равновесия пространственной системы сходящихся сил: алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должны быть равны нулю, т.е.
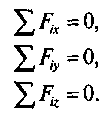
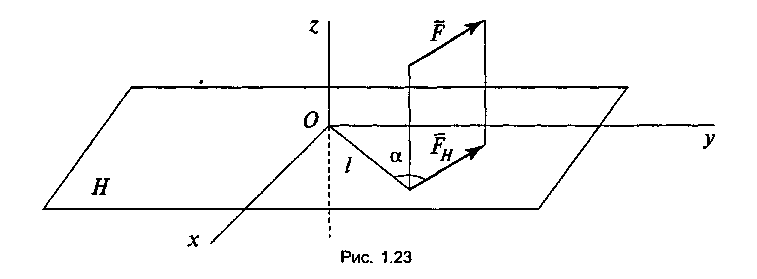
Для того чтобы найти момент силы F относительно оси z , надо спроектировать силу F на плоскость Н, перпендикулярную оси z (рис. 1.23), затем найти момент проекции FH относительно точки О, которая является точкой пересечения плоскости Не осью z . Момент проекции FH и будет являться моментом силы F относительно оси z '.
Моменты сил, перпендикулярных или параллельных оси z , будут равны нулю (рис. 1.24).
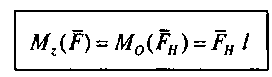
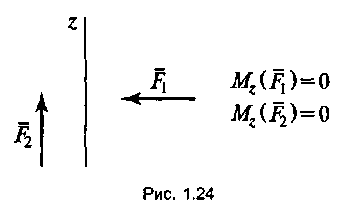 Пространственной системой произвольно расположенных сил называется система сил, линии, действия которых не лежат в одной плоскости и не пересекаются в одной точке. Равнодействующая такой системы сил также равна геометрической сумме этих сил, но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).
Пространственной системой произвольно расположенных сил называется система сил, линии, действия которых не лежат в одной плоскости и не пересекаются в одной точке. Равнодействующая такой системы сил также равна геометрической сумме этих сил, но изображается диагональю сложных объемных фигур (тетраэдр, октаэдр и т.д.).
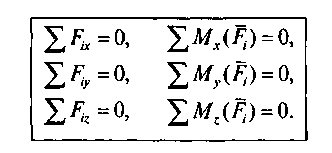
 Условие равновесия пространственной системы произвольно расположенных сил: алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должна быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей координат должна быть равна нулю, т.е.
Условие равновесия пространственной системы произвольно расположенных сил: алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должна быть равна нулю и алгебраическая сумма моментов всех сил относительно тех же осей координат должна быть равна нулю, т.е.
Центры тяжести
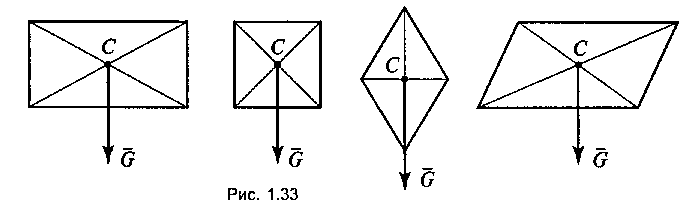 Сила тяжести — это сила, с которой тело притягивается к земле. Центр тяжести — это точка приложения силы тяжести (рис. 1.32). Положение центра тяжести простых геометрических фигур: 1) в прямоугольнике, квадрате, ромбе, параллелограмме — на пе ресечении диагоналей (рис. 1.33);
Сила тяжести — это сила, с которой тело притягивается к земле. Центр тяжести — это точка приложения силы тяжести (рис. 1.32). Положение центра тяжести простых геометрических фигур: 1) в прямоугольнике, квадрате, ромбе, параллелограмме — на пе ресечении диагоналей (рис. 1.33);
2) в треугольнике — на пересечении медиан (рис. 1.34):
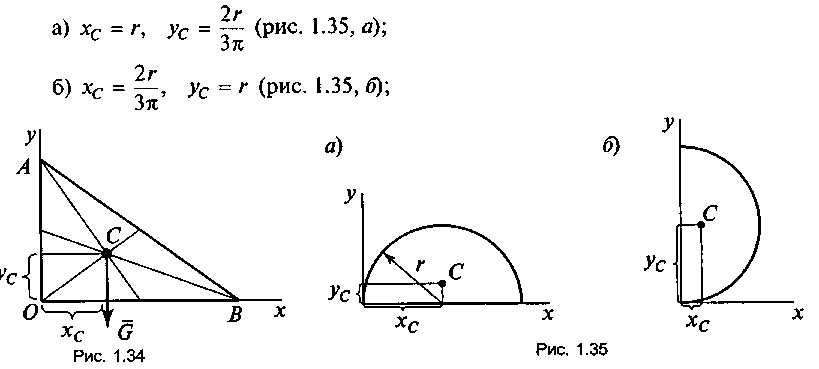
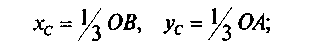
3) в круговом секторе или полукруге — в точке с координатами:
4)в конусе или полной пирамиде — на 1/3 высоты от основания (рис. 1.36):
 Положение центра тяжести плоских фигур прокатных профилей:
Положение центра тяжести плоских фигур прокатных профилей:
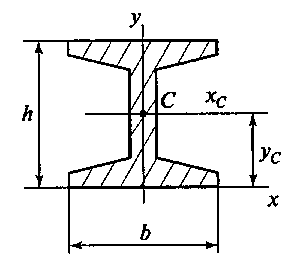
1)в балке двутавровой (рис. 1.37) — в точке c координатами
хс=0, yc = h /2,
 где h — высота двутавра.
где h — высота двутавра.
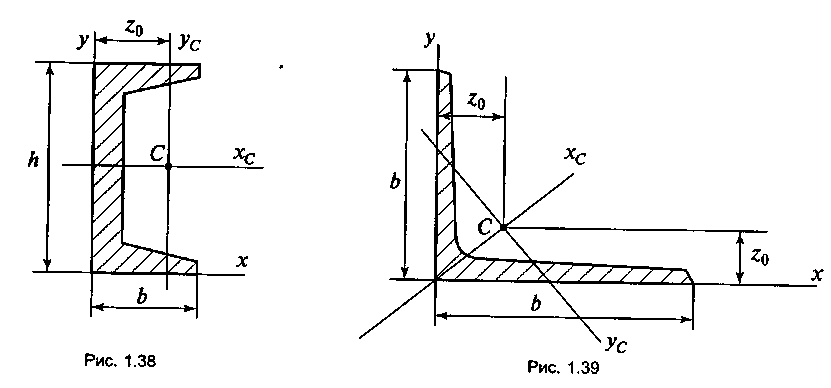
2)в швеллере (рис. 1.38) — в точке с координатами xc = z 0 , yc = h /2,
где h — высота швеллера;
Z 0 — расстояние от центра тяжести и ус до наружной грани стенки;
3)в равнополочном уголке (рис. 1.39) — в точке с координатами XC = YC = Z 0
Если плоская фигура имеет неправильную геометрическую форму, то центр тяжести такой фигуры можно определить двумя способами:
 1)методом подвешивания фигуры на острие;
1)методом подвешивания фигуры на острие;
2) теоретическим методом. Рис.1.37
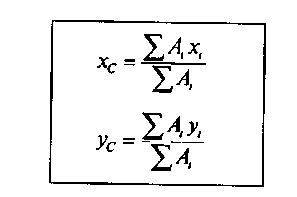 В этом случае плоская фигура разбивается на определенное количество элементарных фигур, имеющих правильную геометрическую форму. Затем определяется положение центра тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты центра тяжести заданной сложной фигуры, используются следующие формулы:
В этом случае плоская фигура разбивается на определенное количество элементарных фигур, имеющих правильную геометрическую форму. Затем определяется положение центра тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты центра тяжести заданной сложной фигуры, используются следующие формулы:
где А i — площади элементарных фигур, на которые разбита сложная фигура;
х i ; у i — координаты центра тяжести каждой элементарной фигуры относительно случайных осей X и Y .
Тест – задания для самопроверки по лекциям № 3 - 4
| 11. Поясните цель приведение силы к точке – |
| 12.Чем отличается произвольная система сил от плоской системы сил (пояснить формулами) – |
| 13. Определите суммарную силу шарнирно-неподвижной опоры если известно Rx = 8 кН ; Ry = 6 кН |
| 14. В чём состоит сущность условия равновесия пространственной системы сил |
| 15. В чем отличие главного вектора системы сил от равнодействующей силы системы сил |
| 16. В чем отличие и в чем сходство между шарнирно-неподвижной опорой и шарнирно – подвижной опорой? |
| 17. Запишите основную форму уравнений равновесия балочной системы |
| 18.Как определяется момент силы расположенной в пространстве относительно оси перпендикулярной заданной плоскости |
| 19. зарисуйте рисунок характеризующий геометрическое условие равновесия пространственной системы сил |
| 20. Запишите уравнения равновесия пространственной системы сил |
| 21. Как определить координаты центра тяжести плоской конструкции если известны площади элементарных фигур из которых состоит конструкция |
Дата: 2019-07-24, просмотров: 1777.