2.1. Формула Ньютона – Лейбница
Вычислять О.И. удобнее и легче по формуле. Для вывода формулы нужно вводить понятие интеграла с переменным верхним пределом, что не входит в данный курс, поэтому без вывода:
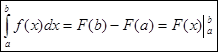
Здесь: F(x) – одна первообразных функции f ( x ), (при C = 0)
F(b) и F(a) – значения первообразной соответственно в точках a и b.
Алгоритм вычисления О.И. – 1) для заданной функции найти первообразную; 2) подставив в нее последовательно сначала верхний, потом нижний пределы, сосчитать F(b) – F(a).
Пример: 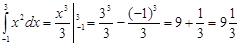
При вычислении определенного интеграла используются те же методы, что и для вычисления неопределенного.
2.2. Практическая работа № 9 «Вычисление определенного интеграла»
· Непосредственное интегрирование
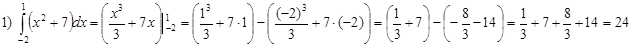
Рекомендуется, не дочитывать числа в каждой скобке, а сначала скобки раскрыть. Часто при этом дроби исчезают.
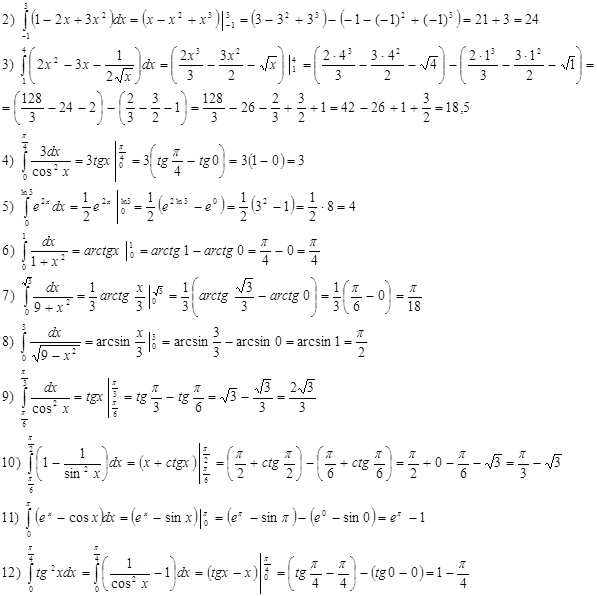
· Метод подстановки
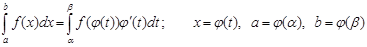
α и β – новые пределы интегрирования. После замены переменной и нахождения интеграла не нужно возвращаться к исходной переменной (в отличие от неопределенного интеграла).
1) 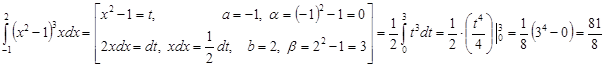 ;
;
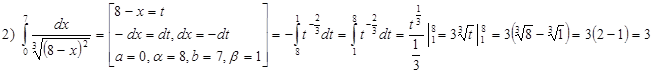
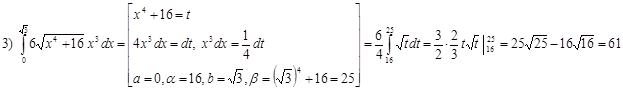
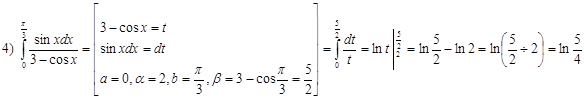
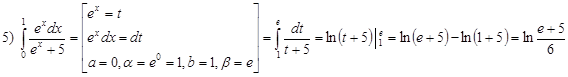
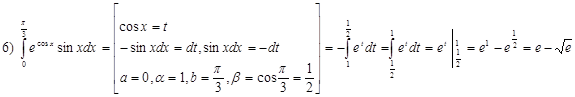
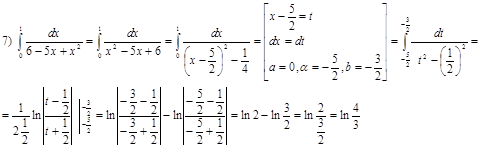
· Интегрирование по частям (необязательно) Формула: 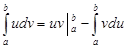
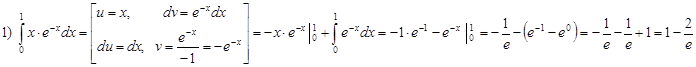
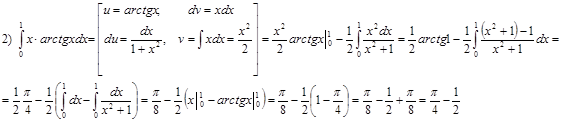
Домашнее задание № 12 «Вычисление определенного интеграла»
Вычислить интегралы:
1. Непосредственное интегрирование
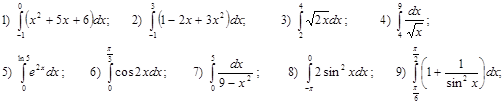
Ответы: 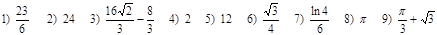
2. Метод подстановки
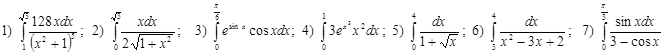
Ответы: 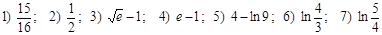
Лекция 3. Геометрическое приложение определенного интеграла. Вычисление площадей
3.1. Вычисление площадей
1) Если фигура ограничена линиями: y = f(x), OX, x = a, x = b (т.е. площадь криволинейной трапеции)
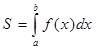
2) Если фигура ограничена графиками двух функций: 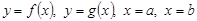
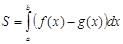
 3) Если фигура ограничена графиками нескольких непрерывных функций – свести задачу к задаче 2).
3) Если фигура ограничена графиками нескольких непрерывных функций – свести задачу к задаче 2).
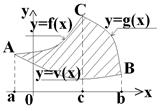
Например: на рисунке фигура ограничена графиками функций 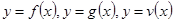
Точкой С разбиваем отрезок [a, b] на два. Тогда:
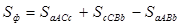 или
или 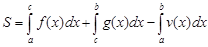
3.2. Практическая работа № 10 «Вычисление площадей плоских фигур»
Найти площадь фигуры, ограниченной линиями:
1) 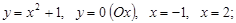 сделаем схематичный рисунок. График функции выше оси абсцисс, значит – это криволинейная трапеция.
сделаем схематичный рисунок. График функции выше оси абсцисс, значит – это криволинейная трапеция.

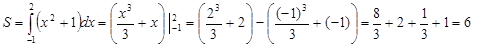
Ответ: 6 ед2
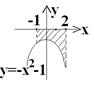 2)
2) 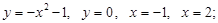
График функции ниже оси абсцисс, значит площадь:
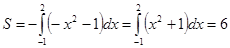 Ответ: 6 ед2
Ответ: 6 ед2
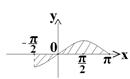 3)
3) 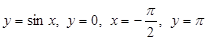 . См. рисунок: на заданном отрезке фигуру разбиваем на две части:
. См. рисунок: на заданном отрезке фигуру разбиваем на две части:
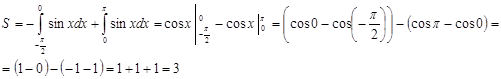 Ответ: 3 ед2
Ответ: 3 ед2
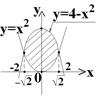
4) 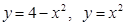 (a ?, b?)
(a ?, b?)
1) Ищем пределы интегрирования: это точки, в которых графики пересекаются. Составляем уравнение: 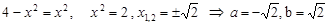 ;
;
2) Фигура ограничена графиками четных функций, значит, она симметрична относительно оси Y. Тогда удобнее найти половину площади и умножить на 2. 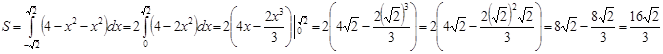 Ответ:
Ответ: 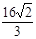
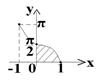 5)
5) 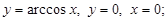 чтобы найти площадь данной фигуры, придется применить интегрирование по частям.
чтобы найти площадь данной фигуры, придется применить интегрирование по частям.
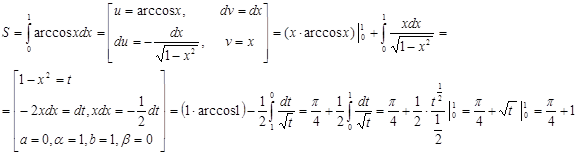
Ответ: 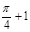
Задание для самостоятельной работы
Найти площадь фигуры, ограниченной линиями: Часть 1.
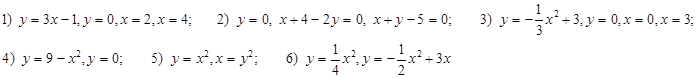 Ответы:
Ответы: 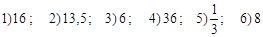 (ед2)
(ед2)
Часть 2.
1) 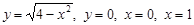 ; 2)
; 2) 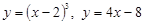 ; 3)
; 3) 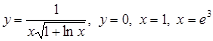 ; 4)
; 4) 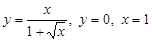 ; 5)
; 5) 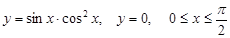
Ответы: 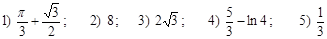 (ед2)
(ед2)
Лекция 4. Геометрическое приложение определенного интеграла. Вычисление объемов
4.1. Вычисление объемов тел вращения
Тело вращения – это тело, полученное вращением плоской фигуры вокруг одной из сторон. В нашем случае вращаемая фигура – это криволинейная трапеция. Вращать ее можно вокруг оси X и вокруг оси Y (тела при этом получаются разные).
Пусть функция f(x) непрерывна на отрезке [a, b]. Тогда объем тела, полученного вращением рассматриваемой криволинейной трапеции:
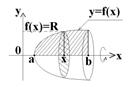 1. Вокруг оси X :
1. Вокруг оси X :
Заштрихованная в диагональ фигура – это исходная криволинейная трапеция.
Заштрихованный эллипс – это круг радиуса R, который получается при вращении выделенного отрезка вокруг оси X. Площадь этого круга:
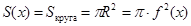
Тогда объем : 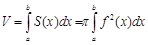
2. Вокруг оси Y : 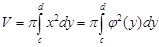
Т.е. здесь нужно выразить x через y и вычислить пределы интегрирования.
4.2. Решение задач
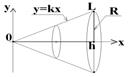 1) Получим знакомую формулу для вычисления объема конуса
1) Получим знакомую формулу для вычисления объема конуса 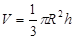
Конус получается вращением прямоугольного Δ LOh вокруг оси OX.
Сверху фигура ограничена прямой; это график линейной функции 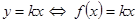
Тогда: 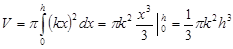
При условии, что 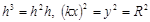 , имеем
, имеем 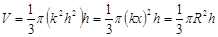
2) Вычислить объем тела, полученного при вращении фигуры, ограниченной линиями: 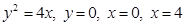 вокруг OX .
вокруг OX .
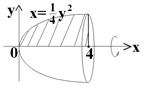 Это тело называется параболоид вращения
Это тело называется параболоид вращения
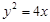 – это верхняя часть параболы
– это верхняя часть параболы 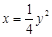
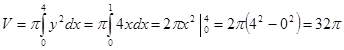 Ответ: 32π ед3
Ответ: 32π ед3
3) Вычислить объем тела, полученного при вращении фигуры, заключенной между графиками функций
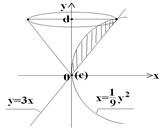
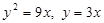 вокруг OY.
вокруг OY.
1. Сначала строим тело, о котором идет речь. Оно получено вращением заштрихованной фигуры вокруг оси Y.
2. Определяем пределы интегрирования: c = o, d = ?
Значение d соответствует точке, в которой пересекаются графики.
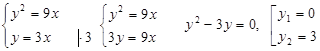 т.е. d = 3
т.е. d = 3
3. Подынтегральная функция:
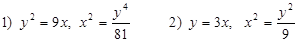
4. По формуле: 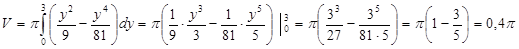
Ответ: 0,4 π ед3
Задание для самостоятельной работы
Вычислить объемы тел, полученных вращением фигур, ограниченных линиями:
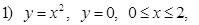 вокруг Ox ;
вокруг Ox ;
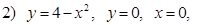 вокруг Oy ;
вокруг Oy ;
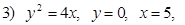 вокруг Ox ;
вокруг Ox ;
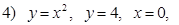 вокруг Oy ;
вокруг Oy ;
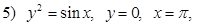 вокруг Ox ;
вокруг Ox ;
Ответы: 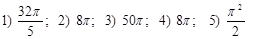 (ед3)
(ед3)
Лекция 5. Дифференциальное и интегральное исчисление в прикладных задачах
Физические задачи
Если 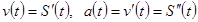 , тогда, если задана формула изменения скорости (ускорения), путь, пройденный телом (скорость) за время
, тогда, если задана формула изменения скорости (ускорения), путь, пройденный телом (скорость) за время 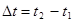 :
: 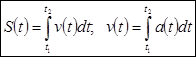 .
.
Задача 1. Тело ускоренно движется по закону 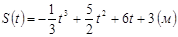 . Найти:
. Найти:
1) Начальную скорость движения;
2) Среднюю скорость за время от 2 с до 4 с;
3) Путь, пройденный телом от начала движения до полной остановки, и ускорение в этот момент.
Решение. 1) 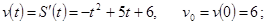
2) 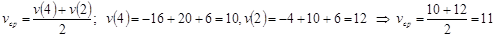 ;
;
3) Тело остановилось – значит, скорость в этот момент времени равна нулю:
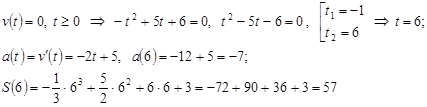
Ответ: 1) 6 м/с, 2) 11 м/с, 3) 57 м, -7 м/с2 (отрицательное ускорение подсказывает, что движение было ускоренно-замедленным).
Задача 2. Скорость тела, движущегося прямолинейно, изменяется по закону: 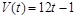 [м/с]. Найти путь, пройденный телом за время от 3-й до 5-й секунды.
[м/с]. Найти путь, пройденный телом за время от 3-й до 5-й секунды.
Решение: 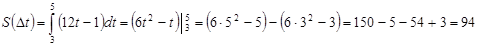
Ответ: 94 м.
Дата: 2019-07-24, просмотров: 317.