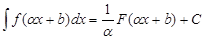Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

РАЗДЕЛ 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Тема 4.1. Производная и ее приложения

Тема 4.2. Дифференциал

Лекция 1. Дифференциал. Определение и геометрический смысл

1.1. Дифференциал

Пусть функция f ( x ) дифференцируема в точке x₀ Î(a, b), т.е. существует .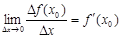

Тогда по теореме о представлении функции в виде суммы ее предела и б.м.ф. (см. раздел 3, тема 3.2.) «Предел функции в точке»: если 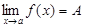, то f(x) = A + α(x)) имеем:

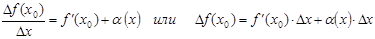
Здесь слагаемые α(x) и Δx есть бесконечно малые более высокого порядка, чем величина 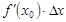. Тогда величина  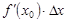  составляет главную часть приращения функции в точке x ₀ . Это и есть дифференциал.

Определение. Дифференциалом функции y = f ( x ) в точке x ₀ называется линейная относительно Δx величина 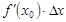, составляющая главную часть приращения функции в точке x₀.

Обозначение: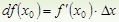

Если функция дифференцируема в каждой точке интервала (a, b), то 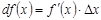  или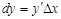

Для функции .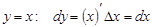

Тогда запись: d f ( x ) = f ^/ ( x ) dx или d y = y ^/ dx

Т.е. дифференциал функции равен произведению производной на дифференциал аргумента.

 

При этом, если f ^/ (x₀) = 0, то d f(x₀) = 0. Здесь f ^/ (x₀) Δx не главная часть приращения функции, т.к. .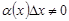

Примеры. Найти дифференциалы следующих функций:

1)

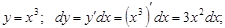
2)

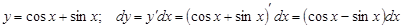
1.2. Дифференциал сложной функции

Если y = f ( u ), u = g ( x ):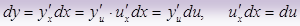

Таким образом, форма дифференциала не зависит от того, является ли аргумент независимой переменной или функцией другого аргумента. Это свойство называется инвариантность дифференциала.

Пример: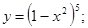

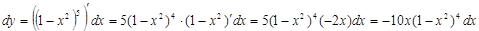
1.3. Основные свойства дифференциала: u и v -дифференцируемые функции

 

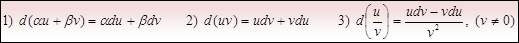
Задание для самостоятельной работы

Найти дифференциалы функций для допустимых значений аргумента:

 

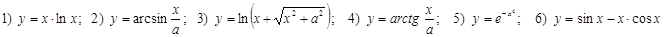
1.4. Геометрический смысл дифференциала

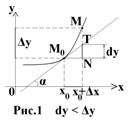
Рассмотрим функцию y = f ( x ), дифференцируемую в точке x ₀ .

Точка x ₀ → x ₀ + Δx , M ₀ → M

M₀T – касательная. Т – точка касательной, соответствующая приращенному аргументу.

Δx – приращение аргумента, Δy – приращение функции.

Тогда из ΔM₀NT, <M₀= α:

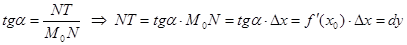
Дифференциал функции в точке x ₀ равен приращению ординаты касательной, которое соответствует приращению аргумента на Δ x .

Дифференциал может быть меньше (рис.1) и больше приращения функции (рис.2)

 

При достаточно малых приращениях аргумента (Δx) можно допустить, что        dy ≈ Δ y ( d f ( x ₀ ) ≈ Δ f ( x ₀ )).

 

Приняв подобное допущение, рассматриваем практическое приложение дифференциала.

Лекция 2. Применение дифференциала к приближенным вычислениям

На практике вычислить дифференциал проще, чем приращение функции. Поэтому, если нужно найти приращение функции в точке вместо величины 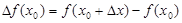   применяют приближенное значение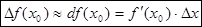

Таблица основных интегралов

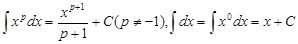
1.	13.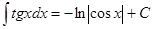
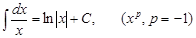
2.	14.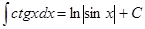
3 .	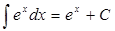15.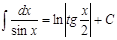
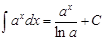
4.	16.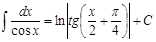
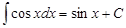
5.	17.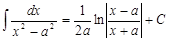
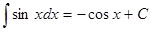
6.	18.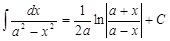
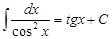
7.	19.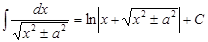
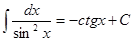
8.	20.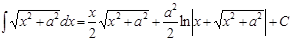
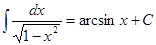
9.	21.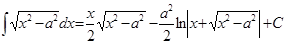
10.
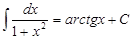
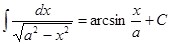
11.	22. Для сложной функции:
12.

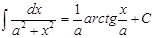
Лекция 2. Методы интегрирования. Непосредственное интегрирование

 

 Существует несколько стандартных методов вычисления интегралов. Непосредственное интегрирование подразумевает вычисление неопределенного интеграла только при помощи свойств интеграла и таблицы основных интегралов.

Примеры. Вычислить интегралы:

 

 

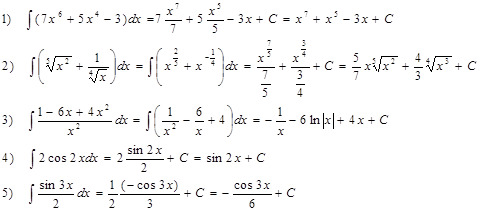
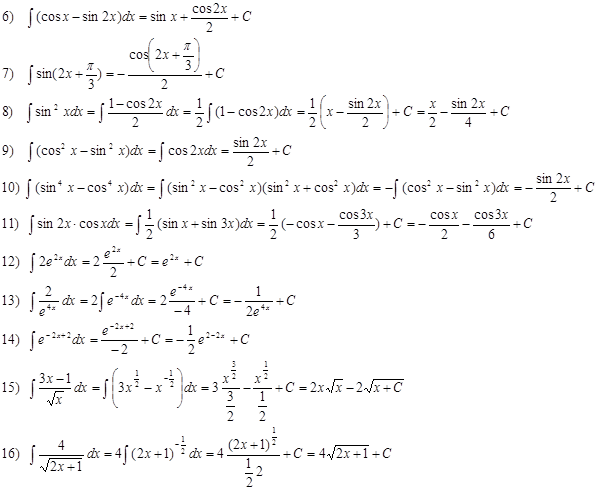
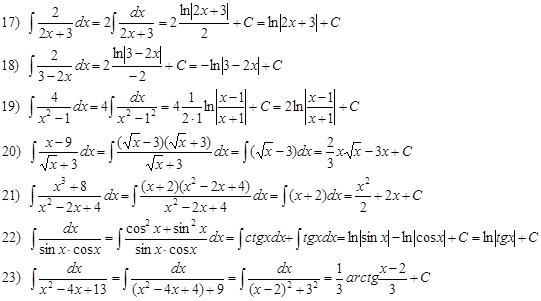
В примере № 20 использована операция «домножения на сопряженное», в примере № 23 – метод выделения полного квадрата:

 

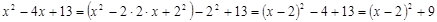
Домашнее задание № 9 «Непосредственное интегрирование»

Вычислить интегралы:

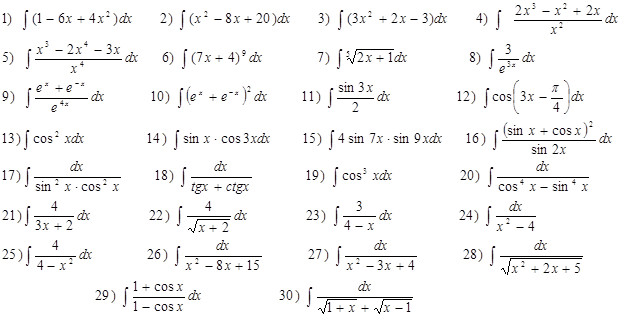
Лекция 3. Методы интегрирования. Метод подстановки

3.1. Интегрирование методом замены переменной (метод подстановки)

Если не удается найти интеграл непосредственно, то интегрируем методом подстановки.

Сущность метода: введением новой переменной интегрирования свести заданный интеграл к новому, который вычисляется непосредственно.

                

При этом должен остаться интеграл, в котором будет только одна переменная. Для этого обозначаем вводимую переменную 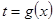 и считаем 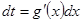. После интегрирования необходимо вернуться к исходной переменной.

               

Пример оформления:

 

 

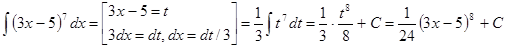
3.2. Практическая работа № 8 «Методы интегрирования»

 

 

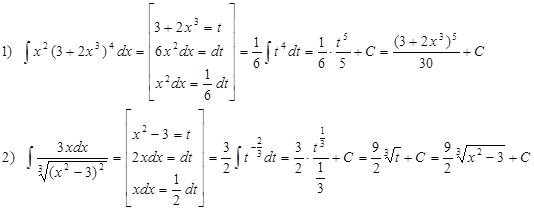
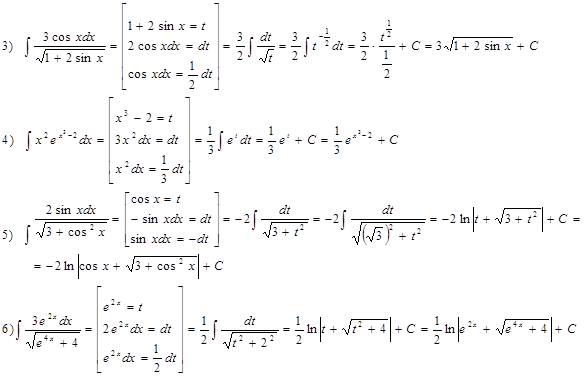
В примере № 7 воспользуемся методом выделения полного квадрата, чтобы свести интеграл к табличному.

 

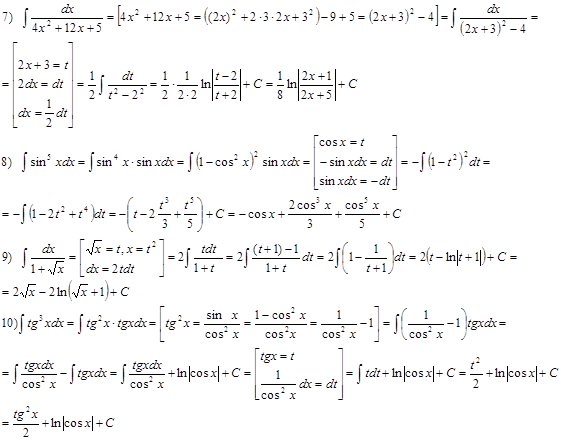
Домашнее задание № 10 «Интегрирование методом подстановки»

Вычислить интегралы:

А)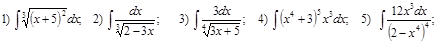    

Б)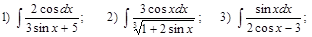    

В)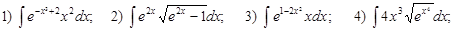     

Г)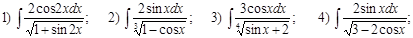     

Д)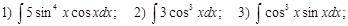    

Е)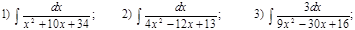    

Ж)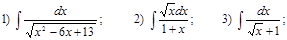  

З)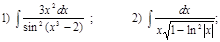             

Ответы:

А):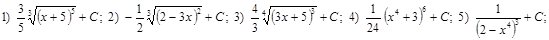

Б):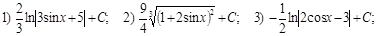

В):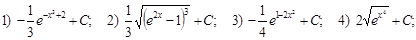

Г):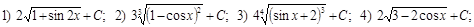

Д):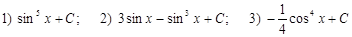

Е):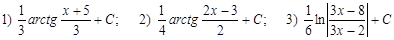

Ж):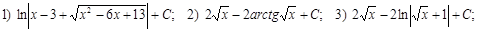

З):

Лекция 4. Методы интегрирования. Интегрирование по частям

4.1. Вывод формулы

Пусть функции 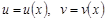 имеют непрерывные производные на промежутке X. Найдем:

а) дифференциал от произведения u ∙ v:

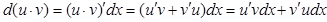                         (1)

б) интеграл от обеих частей равенства (1):

                                       

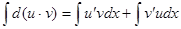
Здесь: 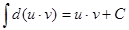      по свойству неопределенного интеграла № 3 (см. Лекцию 1)  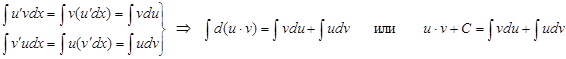  (2)

Тогда: 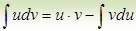            формула интегрирования по частям

 

Таким образом, подынтегральное выражение f ( x ) dx представляется в виде произведения множителей u и dv, т.е. исходно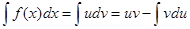

(В правой части постоянную C не пишут, т.к. при интегрировании она появится в du).

 

Алгоритм нахождения интеграла:

1) разбить исходный интеграл на u и dv;

2) найти du и v;

3) вычислить заданный интеграл по формуле.

 

4.2. Типовые задачи

Здесь главное увидеть, что принять за u и что за dv. При этом существуют типовые разбиения в различных видах интегралов.

 

А) В интегралах вида: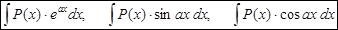

(P(x) – многочлен относительно x, a – некоторое число)

Полагают: u = P ( x ),  все остальное – dv

 

Пример: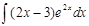

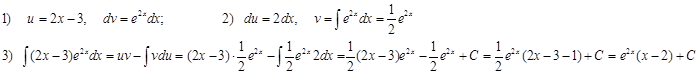
Б) В интегралах вида: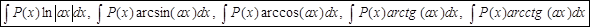

Полагают: P ( x ) dx = dv, все остальное – u

 

Пример: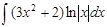   

Решение:

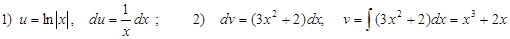
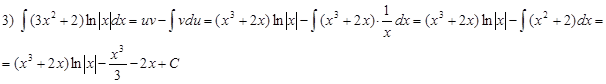
В) В интегралах вида: 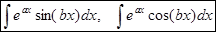, где a и b некоторые числа, за u можно принять любую функцию: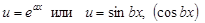

 

Пример: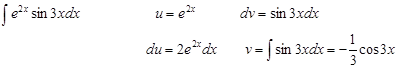 

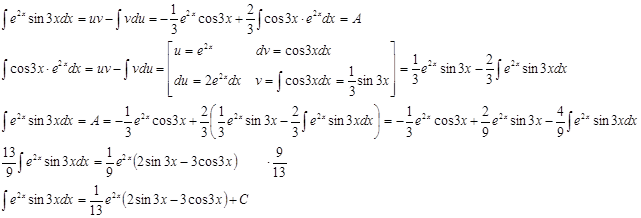
Здесь пришлось применить интегрирование по частям дважды.

Так приходится делать и в случае понижения степени (как правило, тригонометрических функций и многочленов).

Интегралы вида: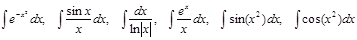

существуют, но не выражаются через элементарные функции.

 

4.3. Решение примеров

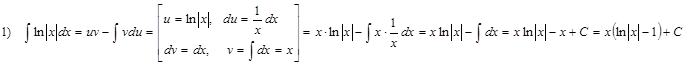
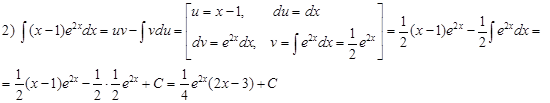
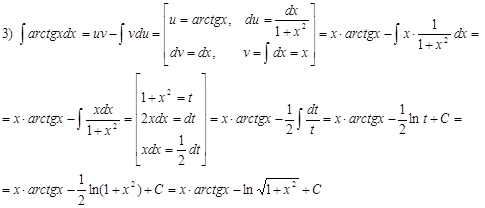
Домашнее задание № 11 «Интегрирование по частям»

 

Вычислить интегралы (в скобках приведены ответы):

 

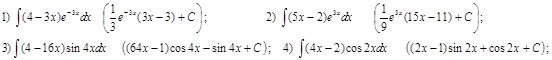
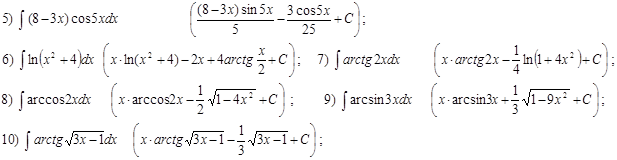
Физические задачи

Если 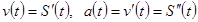, тогда, если задана формула изменения скорости (ускорения), путь, пройденный телом (скорость) за время : .

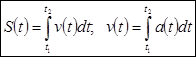Задача 1. Тело ускоренно движется по закону 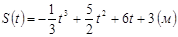. Найти:

1) Начальную скорость движения;

2) Среднюю скорость за время от 2 с до 4 с;

3) Путь, пройденный телом от начала движения до полной остановки, и ускорение в этот момент.

Решение. 1)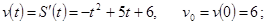

             2) ;

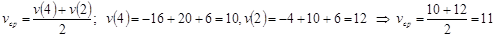             3) Тело остановилось – значит, скорость в этот момент времени равна нулю:   

           

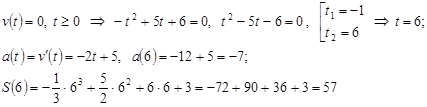
Ответ: 1) 6 м/с, 2) 11 м/с, 3) 57 м, -7 м/с² (отрицательное ускорение подсказывает, что движение было ускоренно-замедленным).

Задача 2. Скорость тела, движущегося прямолинейно, изменяется по закону: 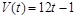 [м/с]. Найти путь, пройденный телом за время от 3-й до 5-й секунды.

Решение: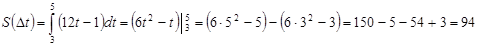

Ответ: 94 м.

 

РАЗДЕЛ 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ