1.1. Таблица производных элементарных функций и правила дифференцирования
| Функция | Производная |
| 1) Постоянная: C | 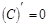
|
| 2) Степенная: xn | 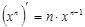
|
Частные случаи: 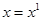
| 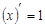
|
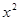
| 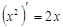
|
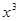
| 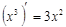
|
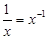
| 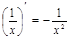
|
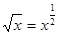
| 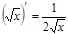
|
3) Показательная: 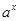
| 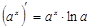
|
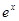
| 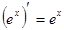
|
4) Логарифмическая: 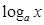 (x > 0) (x > 0)
| 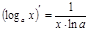
|
Натуральный логарифм: 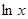 ( x > 0) ( x > 0)
| 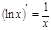
|
5) Тригонометрические: 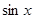
| 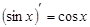
|
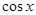
| 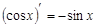
|
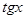
| 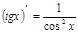
|
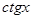
| 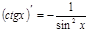
|
| Обратные тригонометрические: | 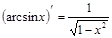 ; ; 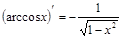
|
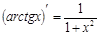 ; ; 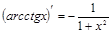
| |
| Правила дифференцирования | |
| 1) Постоянный множитель выносится за знак производной: | 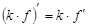
|
| 2) Производная суммы функций: | 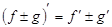
|
| 3) Производная произведения: | 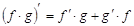
|
| 4) Производная частного: | 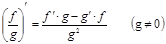
|
| 5) Производная сложной функции: | 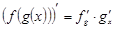
|
| Геометрический смысл производной Значение производной функции в точке х0 равно тангенсу угла наклона касательной (т.е. угловому коэффициенту прямой) | 
|
| Уравнение касательной | 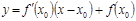 или или 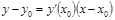
|
| Физический смысл производной Здесь: S ( t ) – заданный закон движения | 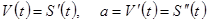
|
1.2. Техника дифференцирования
1. Найти производные функций:
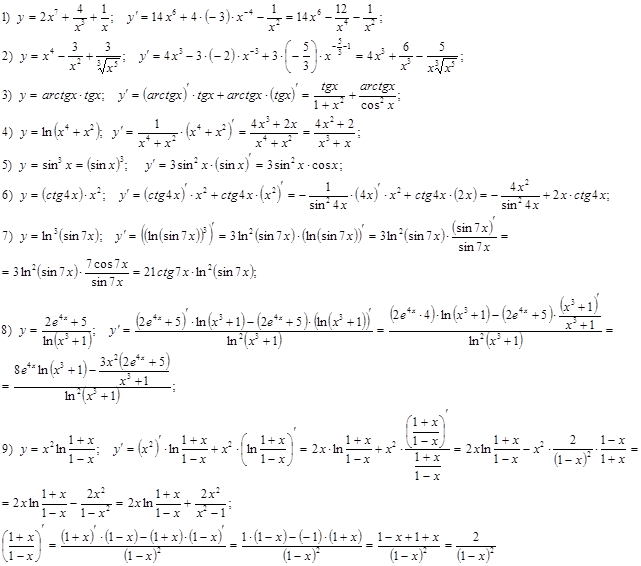
2. Найти значение производной в заданной точке:
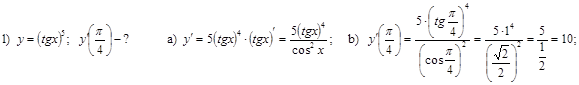
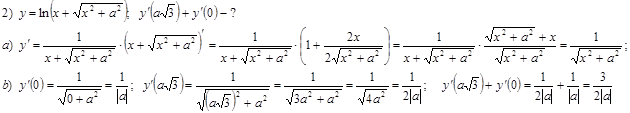
Домашнее задание № 6 «Дифференцирование функций»
Часть 1. Найдите производные функций
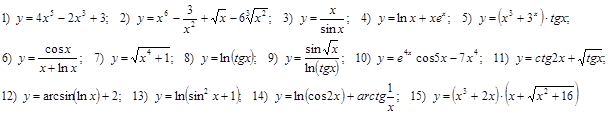
Часть 2. Найдите значение производной функции:
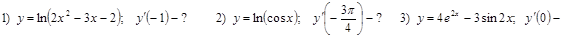 ?
?
Лекция 2. Физический и геометрический смысл первой и второй производной
2.1. Вторая производная – это производная от производной функции; обозначается двумя штрихами т.е. 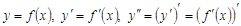 .
.
Например, для функции 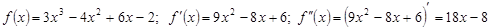 .
.
Вторая производная для первой производной является такой же характеристикой, как первая производная для самой функции. Она характеризует характер монотонности производной и точки экстремума производной. Вторая производная помогает точнее определять поведение функции на отрезке (или на области определения). Исследование функции при помощи второй производной происходит согласно порядку, уже определенному выше. А именно, нужно искать точки, в которых вторая производная обращается в нуль или не существует. Как правило, их называют критические точки второго рода.
Обратите внимание, что для рациональных функций при нахождении последовательно первой и второй производных, степень функции понижается каждый раз на порядок. Т.е., если исследуемая функция третьей степени, то ее первая производная меняется по квадратичному закону, а вторая – по линейному.
А для тригонометрических функций синус и косинус, вторая производная фактически превращается обратно в саму функцию. Например: 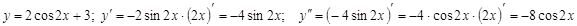 .
.
2.2. Физический смысл первой и второй производной
С точки зрения механики. Если задан закон, по которому путь (или перемещение) материальной точки зависит от переменной – времени, т.е. S ( t ), x ( t ), тогда: первая производная показывает скорость изменения перемещения, а вторая производная – скорость изменения скорости движения, т.е. ускорение.
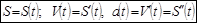 или
или 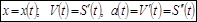
Например:
- Равномерное движение:
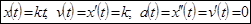 (скорость постоянна, ускорение равно нулю);
(скорость постоянна, ускорение равно нулю); - Равноускоренное движение:
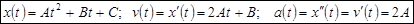 (скорость меняется по линейному закону, ускорение постоянно)
(скорость меняется по линейному закону, ускорение постоянно)
Пример. Движение материальной точки осуществляется по закону 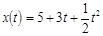 .
.
Найдите: а) начальную скорость движения v 0 ; б) ускорение движения a ( t ); в) время, через которое скорость точки станет равной 12.
Решение. а) 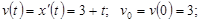 б)
б) 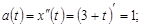 в)
в) 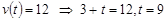
2.3. Геометрический смысл первой и второй производной
2.3.1. Первая производная. Значение производной в точке x 0 равно угловому коэффициенту касательной, построенной к графику соответствующей функции в точке с абсциссой x 0 :
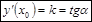 , α – угол наклона касательной к оси абсцисс.
, α – угол наклона касательной к оси абсцисс.
2.3.2. Вторая производная.
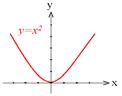
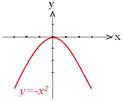 «Наглядным свойством графика функции на некотором промежутке является его выпуклость. График функции может иметь выпуклость как вверх (например, у функции
«Наглядным свойством графика функции на некотором промежутке является его выпуклость. График функции может иметь выпуклость как вверх (например, у функции 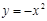 ), так и выпуклость вниз (например, у функции
), так и выпуклость вниз (например, у функции 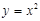 ).
).
Точка, в которой меняется характер выпуклости, называется точкой перегиба функции.
Простейший пример – это функция 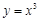 : для нее точка x =0 является точкой перегиба.
: для нее точка x =0 является точкой перегиба.
Если в этой точке провести касательную, то по одну сторону от точки перегиба график функции начинает уходить выше касательной (становится выпуклым вниз), а по другую сторону - график уходит вниз (становится выпуклым вверх).
Точки перегиба появляются в том случае, если первая производная при переходе через эту точку обратилась в нуль или не существовала, но знак не поменяла.
Например: 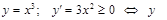 монотонно возрастает. При этом вторая производная:
монотонно возрастает. При этом вторая производная: 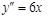 в точке 0 меняет знак; при
в точке 0 меняет знак; при 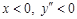 - выпуклость вверх, при
- выпуклость вверх, при 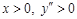 - выпуклость вниз.
- выпуклость вниз.
В общем виде алгоритм нахождения точек перегиба:
· Найти вторую производную функции 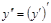 ;
;
· Найти критические точки второго рода, т.е. приравнять вторую производную к нулю и решить уравнение 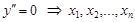 ;
;
· Определить знаки второй производной на получившихся промежутках;
· По знаку второй производной сделать выводы о наличии точек перегиба: это критические точки, в которых вторая производная меняет знак;
· При этом:
Если на промежутке 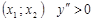 - график функции имеет выпуклость вниз (
- график функции имеет выпуклость вниз ( 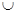 );
);
Если на промежутке 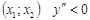 - график функции имеет выпуклость вверх (
- график функции имеет выпуклость вверх (  )
)
2.4. Задачи
Найти точки перегиба функции 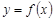 и определить выпуклость графика:
и определить выпуклость графика:
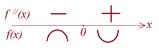 1)
1) 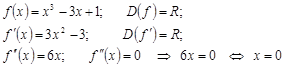
Вывод: x =0 – точка перегиба: 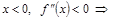 выпуклость графика – вверх;
выпуклость графика – вверх;
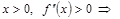 - выпуклость графика – вниз.
- выпуклость графика – вниз.
2) 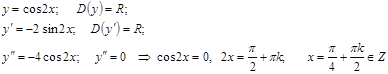
Критических точек второго рода бесконечно много. Однако, учитывая, что наименьший период функции 
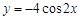 равен π, достаточно определить наличие точек перегиба на этом периоде:
равен π, достаточно определить наличие точек перегиба на этом периоде: 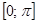
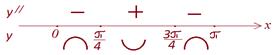 Определение знаков второй производной:
Определение знаков второй производной:
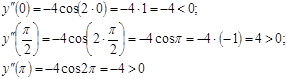
Вывод: точки перегиба 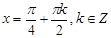 .
.
В точках 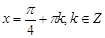 - перегиб с выпуклости графика вверх на выпуклость вниз;
- перегиб с выпуклости графика вверх на выпуклость вниз;
В точках 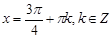 - перегиб с выпуклости графика вниз на выпуклость вверх.
- перегиб с выпуклости графика вниз на выпуклость вверх.
Задание для самостоятельной работы
1) Найти вторую производную функции:
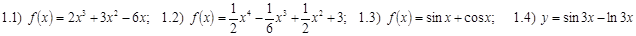 ;
;
2) Найти точки перегиба функции и определить выпуклость графика:
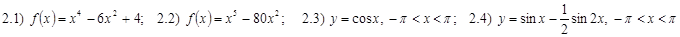
Лекция 3. Исследование функций при помощи производной. Построение графиков
3.1. Схема исследования функции
Дана функция y = f(x). Задача: построить график.
1) Найти область определения функции D(y);
2) Исследовать функцию на четность;
3) Определить, является ли функция периодичной;
4) Исследовать функцию при помощи первой производной, т.е. найти:
· Промежутки возрастания и убывания функции;
· Точки экстремумов и экстремумы;
· При необходимости – наибольшее и наименьшее значения функции на отрезке;
5) Исследовать функцию при помощи второй производной, т.е. найти:
· Точки перегиба и значения функции в этих точках;
· Определить вид выпуклости графика;
6) Найти точки пересечения графика с осями координат:
· С осью Ox – нули функции;
· С осью Oy, y(0);
7) Сосчитать дополнительные точки (в том случае, если невозможно найти нули функции);
8) Найти асимптоты графика;
Если функция достаточно сложная, рекомендуется составить сводную таблицу.
3.2. Практическая работа № 6 «Исследование функции при помощи производной»
Задание. Исследовать по общей схеме функции и построить их графики:
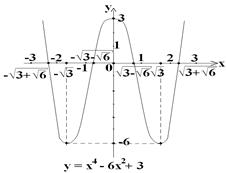
1)  ; функция непрерывна на области определения;
; функция непрерывна на области определения;
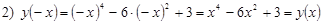 - функция четная (график симметричен относительно Oy);
- функция четная (график симметричен относительно Oy);
3) Функция не является периодичной;
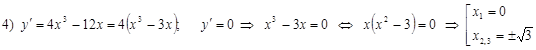
Выводы: ― + ― + y/
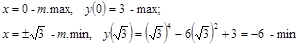 ———○————○————○———> x
———○————○————○———> x
↓ -√3 ↑ 0 ↓ √3 ↑ y
Промежутки убывания и возрастания функции очевидны с рисунка.
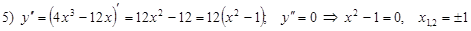

Выводы: x =±1 – точки перегиба; 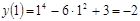
 6) а) Нули функции:
6) а) Нули функции:
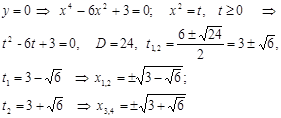
б) точка пересечения с Oy : x =0; y (0)=3
7) Дополнительные точки можно не считать.
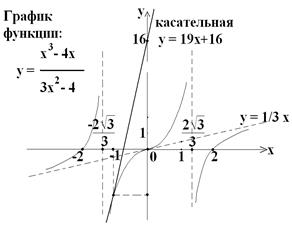
2. 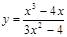 ; Дополнительно: к графику функции построить касательную в точке x = -1.
; Дополнительно: к графику функции построить касательную в точке x = -1.
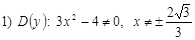 - здесь: функция непрерывна на области определения, а в точках
- здесь: функция непрерывна на области определения, а в точках 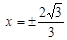 не существует; область определения симметрична, поэтому пункт 2;
не существует; область определения симметрична, поэтому пункт 2;
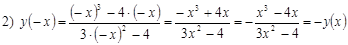 - функция нечетная;
- функция нечетная;
3) Непериодична;
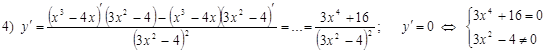 - решений нет, значит, функция ведет себя монотонно на каждом промежутке существования:
- решений нет, значит, функция ведет себя монотонно на каждом промежутке существования: 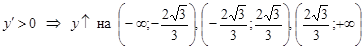
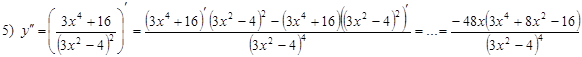
Ищем критические точки 2 рода: 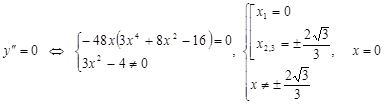
+ не сущ. ― + не сущ. ― y //
———○————○————○————> x
U -2√3/3 ∩ 0 U 2√3/3 ∩ y x = 0 точка перегиба y (0) = 0;
6) а) Нули функции: 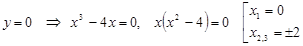 ;
;
б) Точка пересечения графика с Oy : x = 0, y (0) = 0
7) Дополнительные точки – не нужны;
8) Асимптоты:
· 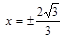 - вертикальные асимптоты;
- вертикальные асимптоты;
· Наклонная асимптота: 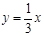 . Чтобы найти наклонную асимптоту, нужно вычислить коэффициенты k и b линейной функции
. Чтобы найти наклонную асимптоту, нужно вычислить коэффициенты k и b линейной функции
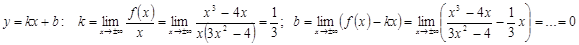
Задание 2. Касательная: 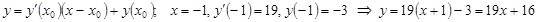
Составим сводную таблицу:
| x | (-¥,-2√3/3) | -2√3/3 | (-2√3/3,0) | 0 | (0,2√3/3) | 2√3/3 | (2√3/3, ¥) |
| y | ↑ | → ±¥ | ↑ | 0 | ↑ | → ±¥ | ↑ |
| y / | + | Нет | + | 1 | + | Нет | + |
| y // | + | Нет | ― | 0 | + | Нет | ― |
| выпуклость | U | Вертик. асимптота | ∩ | Точка перегиба | U | Вертик. асимптота | ∩ |
Домашнее задание № 7 «Исследование функций при помощи производной»
Исследуйте функции и постройте их графики:
1) 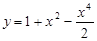 ; 2)
; 2) 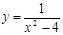 ; 3)
; 3) 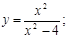 4)
4) 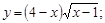 5)
5) 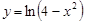
Тема 4.2. Дифференциал
Лекция 1. Дифференциал. Определение и геометрический смысл
1.1. Дифференциал
Пусть функция f ( x ) дифференцируема в точке x0 Î(a, b), т.е. существует 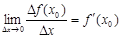 .
.
Тогда по теореме о представлении функции в виде суммы ее предела и б.м.ф. (см. раздел 3, тема 3.2.) «Предел функции в точке»: если 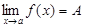 , то f(x) = A + α(x)) имеем:
, то f(x) = A + α(x)) имеем:
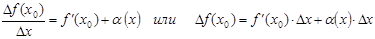
Здесь слагаемые α(x) и Δx есть бесконечно малые более высокого порядка, чем величина 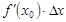 . Тогда величина
. Тогда величина 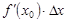 составляет главную часть приращения функции в точке x 0 . Это и есть дифференциал.
составляет главную часть приращения функции в точке x 0 . Это и есть дифференциал.
Определение. Дифференциалом функции y = f ( x ) в точке x 0 называется линейная относительно Δx величина 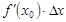 , составляющая главную часть приращения функции в точке x0.
, составляющая главную часть приращения функции в точке x0.
Обозначение: 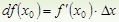
Если функция дифференцируема в каждой точке интервала (a, b), то 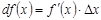 или
или 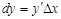
Для функции 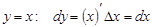 .
.
Тогда запись: d f ( x ) = f / ( x ) dx или d y = y / dx
Т.е. дифференциал функции равен произведению производной на дифференциал аргумента.
При этом, если f / (x0) = 0, то d f(x0) = 0. Здесь f / (x0) Δx не главная часть приращения функции, т.к. 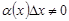 .
.
Примеры. Найти дифференциалы следующих функций:
1) 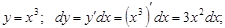
2) 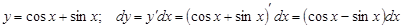
1.2. Дифференциал сложной функции
Если y = f ( u ), u = g ( x ): 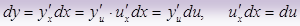
Таким образом, форма дифференциала не зависит от того, является ли аргумент независимой переменной или функцией другого аргумента. Это свойство называется инвариантность дифференциала.
Пример: 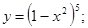
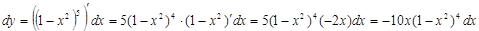
1.3. Основные свойства дифференциала: u и v -дифференцируемые функции
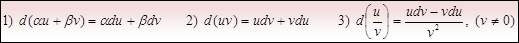
Задание для самостоятельной работы
Найти дифференциалы функций для допустимых значений аргумента:
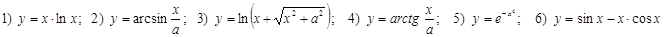
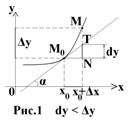 1.4. Геометрический смысл дифференциала
1.4. Геометрический смысл дифференциала
Рассмотрим функцию y = f ( x ), дифференцируемую в точке x 0 .
Точка x 0 → x 0 + Δx , M 0 → M
M0T – касательная. Т – точка касательной, соответствующая приращенному аргументу.
Δx – приращение аргумента, Δy – приращение функции.
Тогда из ΔM0NT, <M0= α:
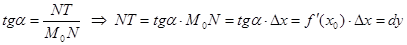
 Дифференциал функции в точке x 0 равен приращению ординаты касательной, которое соответствует приращению аргумента на Δ x .
Дифференциал функции в точке x 0 равен приращению ординаты касательной, которое соответствует приращению аргумента на Δ x .
Дифференциал может быть меньше (рис.1) и больше приращения функции (рис.2)
При достаточно малых приращениях аргумента (Δx) можно допустить, что dy ≈ Δ y ( d f ( x 0 ) ≈ Δ f ( x 0 )).
Приняв подобное допущение, рассматриваем практическое приложение дифференциала.
Дата: 2019-07-24, просмотров: 392.