Кароче есть несущее колебание v₀( t ) = Vсоs(ωt +φ).

У него есть амплитуда, частота и фаза (видим где), ну и кароче можно модулировать все три, а надо угол (фазу или частоту)

Ну и кароче для частотной частота заменяется на такую вот функцию (сразу представляем модулирующий сигнал S(t) как гармонику):

ω (t) = ω+ k _{Ч M} S ( t ) = ω + Δω cos Ωt,                       (5)

где k _{Ч M} – коэффициент пропорциональности; величина Δω = k _{Ч M} S –называется девиацией частоты (максимальное откло­нение частоты модулированного сигнала от частоты несущего коле­бания).

Ну и смотрим кароче как частота меняется:

Рис. 2.12. а, б – Формирование ЧМ-сигнала

При фазовой модуляции заменяем фазу: φ (t) = φ + k _{Ф M} S ( t ) = φ + Δ φ cos Ωt,                (6)

где k _{Ф M} – коэффициент пропорциональности, Δφ = k _{Ф M} S = М_{Ф M} – индекс фазовой модуляции.

Рисунок там примерно такой же, ну тока там подразорваный незаметно.

На самом деле у сигнала можно взять частоту и фазу и запихать это в полную фазу сигнала.

v ₀ ( t ) = Vcos(ωt + φ) = VcosΨ( t ),

где φ – начальная фаза колебания, a Ψ(t) – его полная фаза. Между фазой Ψ(t) и частотой ω существует связь:

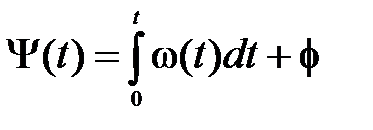                                 (7)

Подставим в (7) выражение (5) для ω(t) при частотной моду­ляции:

Ψ( t ) = ω(t)+ (Δω/Ω) sinΩt.

Величина М_чм = Δω/Ω называется индексом частотной моду­ляции.

Частотно-модулированное колебание запишется в виде:

v ( t ) = Vcos (ωt + М_чм sin Ωt + φ).                  (8)

Фазомодулированное колебание с учетом (6) для φ( t ) сле­дующее:

v ( t ) = Vcos (ωt + М_фм sinΩt + φ).                  (9)

Ну и кароче если сравнивать (8) и (9), то во виду там хуй пойми какая модуляция частотная, а какая фазовая, поэтому обе – угловые, а М_ЧМ и М_ФМ – индексы угловой модуляции.

Качрое если все это понараскрывать (ну там скобки всякие и т.п.), получим:

v(t) = V{I₀(M)cosωt + I₁(M)cos(ω+Ω)t + I₁(M)cos(ω-Ω)t+I₂(M₂)cos(ω+2Ω)t +

+ I₂(M)cos(ω+ 2Ω)t +I₃(W)cos(ω+3Ω)t +I₃₍M)cos(ω-3Ω)t+ ...}.

И видим что угломодулированый сигнал состоит из дофига гармоник, в которых М – индекс угловой модуляции (подставляем там либо Мчм либо Мфм в зависимости от вида модуляции. Амплитуды гармоник в этом выражении определяются некоторыми коэффициентами I_k ( M )_, значения кото­рых при различных аргументах приводятся в специальных справоч­ных таблицах. Чем больше М, тем шире спектр модулированного ко­лебания.

Таким образом, спектр модулированной несущей при угловой модуляции даже при гармоническом первичном сигнале s ( t ) со­стоит из бесконечного числа дискретных составляющих, образую­щих нижнюю и верхнюю боковые полосы спектра, симметричные относительно несущей частоты и имеющие одинаковые амплитуды (рис. 2.13.).

Амплитуда еще вроде там складывается из амплитуды модулирующего колебания и амплитуды информационного, но хер знает.

Рис. 2.13. – Спектр УМ-сигнала

В случае, если первичный сигнал s( t ) имеет форму, отличную от синусоидальной, и занимает полосу частот от Ω_min до Ω_{m ax}, то спектр модулированного колебания при угловой модуляции будет иметь еще более сложный вид.