1. Непрерывный непрерывного времени;
2. Непрерывный дискретного времени;
3. Дискретный непрерывного времени;
4. Дискретный дискретного времени.
Непрерывные сигналы непрерывного времени называют сокращенно непрерывными (аналоговыми) сигналами. Они могут изменяться в произвольные моменты, принимая любые значения из непрерывного множества возможных значений (рис. 2.1.).
| t |
| s(t) |
Рис. 2.1. – Непрерывный сигнал непрерывного времени
Непрерывные сигналы дискретного времени могут принимать произвольные значения, то изменяются только в определенные, наперед заданные (дискретные) моменты t 1 , t 2 , t 3 , ... (рис. 2.2.).
| s(t) |
| t |
| t1 |
| t2 |
| t3 |
| t4 |
| t5 |
| t6 |
Рис. 2.2. – Непрерывный сигнал дискретного времени
Дискретные сигналы непрерывного времени отличаются от предыдущих тем, что они могут изменяться в произвольные моменты, но их величины принимают только конкретные разрешенные (дискретные) значения (уровни).
Дискретные сигналы дискретного времени, сокращенно дискретные (рис. 2.3.), в дискретные моменты могут принимать только конкретные разрешенные (дискретные) значения (уровни).
| s(t) |
| t |
| t1 |
| t2 |
| t3 |
| t4 |
| t5 |
| t6 |
| t7 |
Рис. 2.3. – Дискретный сигнал дискретного времени
Сообщение с помощью специальных датчиков обычно преобразуется в первичный электрический сигнал b(t)
в некоторых случаях сигнал непосредственнопередается по линиям связи когда для передачи на большие расстояния первичный сигнал преобразуют высокочастотный
17. Ряд Фурье, его формы, свойства спектров. Преобразование Фурье и его свойства.
Определение ряда Фурье
Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функцииf (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
1.Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
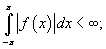
2.Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).
Если x0 − точка разрыва, то ряд Фурье сходится к значению
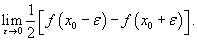
Ряд Фурье функции f (x) представляется в виде
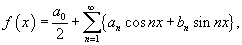
где коэффициенты Фурье a0, an и bn определяются формулами
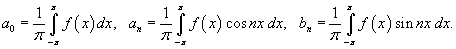
Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя an и bn новыми переменными dn и φn или dn и θn , где
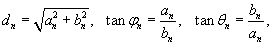
можно, соответственно, записать
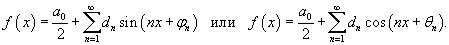
Преобразование Фурье
Итак, преобразование Фурье бывает двух видов: дискретное и непрерывное. Непрерывное используется математиками в аналитических исследованиях, дискретное применяется во всех остальных случаях.
Непрерывное преобразование Фурье - преобразование, которое применяется к функции h(t), заданной на интервале 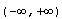 . В результате получается функция H(f):
. В результате получается функция H(f):
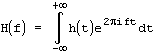
также существует обратное преобразование, которое позволяет по образу H(f) восстановить исходную функцию h(t):
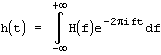
Очевидно, что образ H(f) является комплексной функцией вещественного аргумента, но также и h(t) может принимать не только вещественные, но и комплексные значения.
Применение преобразования Фурье является столь обширной темой, что этот вопрос не будет подниматься в этой статье. Можно только перечислить несколько областей: анализ сигналов, фильтрация, ускоренное вычисление корелляции и свертки, использование в алгоритмах быстрого умножения чисел, и во многих других случаях оно также находит свое применение.
Свойства непрерывного преобразования Фурье
В таблице ниже описана связь свойств прообраза h и образа H.
| Если | То |
| h(t) вещественная | H(-f) = H ·(f) |
| h(t) чисто мнимая | H(-f) = -H ·(f) |
| h(t) четная | H(f) четная |
| h(t) нечетная | H(f) нечетная |
| h(t) вещественная и четная | H(f) вещественная и четная |
| h(t) вещественная и нечетная | H(f) чисто мнимая и нечетная |
| h(t) чисто мнимая и четная | H(f) чисто мнимая и четная |
| h(t) чисто мнимая и нечетная | H(f) вещественная и нечетная |
Следующая таблица показывает, как меняется образ при изменении прообраза. Пусть запись 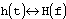 обозначает, что H(f) является образом h(t). Тогда имеют место следующие отношения:
обозначает, что H(f) является образом h(t). Тогда имеют место следующие отношения:
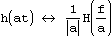
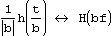
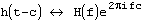
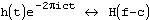
Следующий набор свойств относится к операциям свертки и корелляции. Свертка функций g и h определяется, как 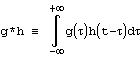 . Корелляция функций g и hопределяется, как
. Корелляция функций g и hопределяется, как 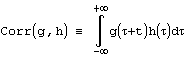 . В таком случае имеют место следующие отношения:
. В таком случае имеют место следующие отношения:
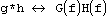
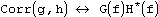
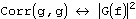
Дискретное преобразование Фурье
С непрерывным преобразованием Фурье удобно работать в теории, но на практике мы обычно имеем дело с дискретными данными. Очень часто у нас дано не аналитическое выражение преобразуемой функции, а лишь набор её значений на некоторой сетке (обычно на равномерной). В таком случае приходится делать допущение, что за пределами этой сетки функция равна нулю, и аппроксимировать интеграл интегральной суммой:
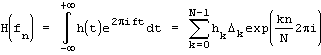
В случае равномерной сетки эта формула упрощается. Также на равномерной сетке обычно избавляются от шага, чтобы получить безразмерную формулу:
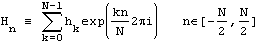
Обратное преобразование в таком случае будет иметь вид
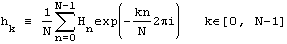
При внимательном рассмотрении можно заметить, что индекс при Hn принимает N+1 значение, в то время как при hk - только N значений. Таким образом, как будто бы получается, что функция H содержит в себе больше информации, чем h. На самом деле это не так, поскольку значения H-N/2 и HN/2 совпадают.
Определенное таким образом, дискретное преобразование Фурье сохраняет практически все свойства непрерывного (разумеется, с учетом перехода к дискретному множеству).
Дата: 2019-07-23, просмотров: 640.