Химический элементМассовое число изотопа с самым долгим периодом полураспадаПериод полураспада84 — полоний[209]103 года85 — астатин[210]8,3 часа86 — радон[222]3,8 дня87 — франций[223]22 минуты88 — радий[226]1 620 лет89 — актиний[227]21,2 года91 — протактиний[231]32 480 лет
Радиоактивное датирование
Изотопы свинца поменяли не только представления химиков об атомных весах, но и представления геологов об истории Земли.
В 1907 году американский физик Бертрам Борден Болтвуд (1870–1927) предложил вычислять возраст полезных ископаемых по радиоактивным рядам.
Предположим, что столько-то лет назад под действием морской седиментации или вулканической активности на поверхности земли сформировался слой застывшей породы, содержащей уран или торий. Атомы урана или тория оказались внутри этого слоя «в ловушке». Атомы свинца, образующиеся в результате распада урана и тория, также окажутся «в ловушке».
На протяжении всего времени с момента отвердевания слоя породы атомы урана или тория будут распадаться, а содержание свинца соответственно увеличиваться. То есть со временем соотношение уран/свинец и торий/свинец в слое будет увеличиваться.
К этому времени Резерфорд уже разработал концепцию полураспада, поэтому стало ясно, что это соотношение будет увеличиваться с известной скоростью. Таким образом, зная величину соотношения урана/свинца или же тория/свинца в любой произвольный момент времени (например, в настоящий), можно вычислить, сколько прошло времени с момента застывания породы. А поскольку периоды полураспада урана–238 и тория–232 чрезвычайно длинные, можно определить возраст до нескольких миллиардов лет.
Основная сложность здесь заключалась в том, что не все атомы свинца, содержащиеся в породе, образовались в результате распада урана или тория, ведь их произвольная часть могла присутствовать в породе в момент застывания наравне с ураном и торием. Такой примордиальный свинец не имеет никакого отношения к распаду урана и тория и приводит к появлению серьезных ошибок при расчетах.
Проблему удалось обойти, определив с помощью масс-спектрографа относительное содержание свинца в нерадиоактивной породе. Выяснилось, что этот свинец состоит из четырех стабильных изотопов свинца с массовыми числами 204, 206, 207 и 208, причем свинец–204 достигает 1,48% (1/67,5 ) от общей массы.
К счастью, свинец–204 не является конечным продуктом ни одного из радиоактивных рядов, значит, на его содержание радиоактивность не влияет. Теперь, если определить содержание в радиоактивной породе свинца–204 и умножить это число на 67,5, то полученное значение будет являться общим количеством присутствующего в породе примордиального свинца. Все, что свыше, является свинцом, образовавшимся в процессе радиоактивного распада.
По соотношению урана/свинца (и учитывая содержание свинца–204) удалось обнаружить застывшие породы, возраст которых более 4 000 000 000. Это является лучшим доказательством того, что Земля образовалась миллиарды лет назад.
Конечно же уран и торий далеко не самые распространенные элементы, и породы с достаточным для точного определения возраста содержанием урана и тория можно обнаружить только в строго определенных местах. Однако определять возраст можно и по рубидию–87, и по калию–40. Оба этих элемента обладают длительным периодом полураспада и в природе встречаются гораздо чаше, нежели уран и торий. В случае с рубидием–87 определяется соотношение рубидий/стронций, так как стронций–87 является конечным продуктом распада рубидия–87. (Количество примордиального стронция определить невозможно, так как другие изотопы стронция, присутствующее в породе, в процессе радиоактивного распада не образуются.) Ученым удалось найти содержащие рубидий минералы, застывшие более 4 000 000 000 лет назад.
С калием–40 не все так просто. В большинстве случаев калий–40 распадается до кальция–40, но содержание кальция–40 в земной коре слишком высоко, чтобы отличить кальций–40, образовавшийся в процессе радиоактивного распада, от примордиального кальция–40. Однако определенное количество кальция–40 путем К-захвата превращается в аргон–40 (ниже).
Аргон — один из содержащихся в атмосфере благородных газов. Все эти газы, за исключением аргона–40, встречаются на Земле в исчезающе малых количествах. Возможно, что за заре своей истории Земля могла удерживать лишь твердые химические соединения, в то время как газообразные вещества просто «улетали», либо из-за малой массы, либо из-за высокой температуры планеты. А благородные газы как раз и не образуют никаких химических соединений.
С другой стороны, аргон–40 составляет около 1% атмосферы. Это значит, что аргон–40 образовался уже после того, как масса и температура Земли приблизились к современному значению (то есть когда у Земли появилась способность удерживать благородные газы). Скорее всего, аргон–40 появился в процессе распада калия-40. Если подсчитать, сколько времени для этого понадобилось, то получится, что Земля в ее современном облике существует уже не менее 4 000 000 000 лет.
Итак, различные методы вычисления возраста дают одну и ту же цифру, которая и является общепринятой на сегодняшний день.
Ядерные реакции
Пока атом считался неделимой частицей, было ясно, что его структуру невозможно изменить в лабораторных условиях за отсутствием таковой. Однако как только обнаружилось, что атом состоит из огромного количества упорядоченных субатомных частиц, у ученых зародилась мысль о том, что этот порядок можно каким-либо образом изменить.
Порядок электронов внешних оболочек атомов изменить довольно просто. Для этого достаточно заставить атомы и молекулы сталкиваться между собой, что ученым удалось сделать еще в XIX веке, подвергая атомы и молекулы нагреванию. Здесь безраздельно правили химики: обычные химические реакции происходят именно за счет перераспределения электронов.
А можно ли перестроить структуру самого ядра? Столь фундаментальная перестройка атома элемента приведет к его превращению в атом другого элемента.
Для того чтобы при столкновении двух атомов их ядра соприкоснулись, преодолев «подушку» из электронов, нужно подвергнуть эти атомы нагреванию до чрезвычайно высокой температуры. К счастью, в XX веке был найден способ обойтись и без высоких температур. Радиоактивные элементы испускают субатомные частицы и при комнатной температуре. Одна из таких частиц — альфа-частица — как раз и является «голым» атомным ядром (атома гелия).
Конечно же направить альфа-частицу в определенное атомное ядро невозможно, но с точки зрения статистики из достаточно большого количества альфа-частиц хотя бы несколько попадут в ядра. Исследуя такие столкновения и «почти» столкновения, Резерфорд и разработал концепцию атома с атомным ядром и рассчитал размер ядра (см. гл. 4).
С другой стороны, столкновения, в результате которых атом и альфа-частица лишь отклоняются или отталкиваются друг от друга, не приводят к изменениям ни того ни другого.
Здесь нужно нечто большее. После серии экспериментов, результаты которых были опубликованы в 1919 году, Резерфорд доказал, что иногда это «нечто большее» все-таки происходит. В начале своих опытов Резерфорд поместил источник альфа-частиц в закрытый цилиндр, один конец которого был покрыт слоем сульфида цинка.
Когда альфа-частица ударяется о сульфид цинка, возникает вспышка люминесценции, или сцинтилляция (мерцание). Это происходит потому, что за счет кинетической энергии альфа-частицы происходит возбуждение молекулы цинка, а возвращаясь в свое прежнее состояние, молекула испускает фотон видимого света. (Впервые это явление наблюдал Беккерель в 1899 году. Позже такой способ стали применять при производстве светящихся объектов. Смесь небольшого количества соединения радия с сульфидом цинка или некоторых других веществ дает свечение, легко заметное в темноте. Самым «писком» 1920-х годов стали часы, на циферблатах которых цифры были нанесены такими вот люминесцентными материалами.)
Если рассматривать мерцающий экран в темноте (когда глаза привыкли к темноте и легко замечают даже слабый свет) с помощью лупы, то можно увидеть каждую вспышку в отдельности. Учитывая, что каждая вспышка вызвана попавшей в экран альфа-частицей, то, подсчитав количество вспышек в заданной области за определенное время, можно определить скорость распада некоторой массы радиоактивного вещества и с помощью этого выяснить, например, период полураспада данного вещества. Прибор, который Резерфорд использовал в своих экспериментах, получил название сцинтилляционный счетчик.
В современных сцинтилляционных счетчиках используются более эффективные сцинтилляторы, а вспышки подсчитываются с помощью фотоэлементов и электроники.
Если же в трубке присутствует газ (например, углекислый или кислород), количество вспышек на экране становится меньше. Это происходит потому, что, сталкиваясь с молекулами газа, альфа-частицы замедляются и некоторые из них присоединяют электроны и становятся обычными атомами гелия. Поэтому до экрана «добирается» меньше частиц, и уровень их кинетической энергии ниже.
Однако если заполнить трубку водородом, то на экране время от времени начинают появляться очень яркие вспышки. Это можно объяснить тем, что иногда альфа-частица сталкивается с ядром водорода (то есть с протоном) и тот, оставив свой электрон, устремляется вперед. В этом случае скорость протона будет гораздо выше, чем у тяжелых ядер углерода и кислорода, и достаточной для того, чтобы при его столкновении с экраном возникла яркая вспышка.
Резерфорд обнаружил, что если заполнить трубку азотом, то на экране также появляются фотонные вспышки. Альфа-частица не могла толкнуть ядро атома азота сильнее, чем ядра углерода или кислорода, но вполне могла выбить из него протон, который и устремлялся к экрану.
В 1925 году английский физик Патрик Блэкетт (1897–1974) доказал это. Он бомбардировал альфа-частицами атомы азота внутри камеры Вильсона. В большинстве случаев альфа-частица оставляла за собой след из водяных капель, не сталкиваясь ни с одним ядром, и, когда ее энергия уменьшалась, присоединяла электроны и исчезала. Однако одна из 350 000 альфа-частиц все же встречала на своем пути препятствие.
В этом случае след ее траектории раздваивался на конце. Один конец был тоньше и довольно длинный. Это — ионизирующий протон, с меньшим, чем у альфа-частицы, зарядом (+1 против +2). Второй след был толстый и короткий. Это — отскочившее ядро атома азота, лишенное большинства электронов, благодаря чему оно получило высокий положительный заряд и соответственно сильные ионизирующие свойства. Тем не менее оно двигалось медленно и, быстро набрав электроны, лишилось этих свойств. Никаких следов альфа-частицы не было, значит, она присоединилась к ядру атома азота.
В 1919 году Резерфорд стал первым, кому удалось изменить структуру атомного ядра, то есть провести первую искусственную ядерную реакцию. (Это что-то вроде «ядерной химии»: нуклоны перераспределяются аналогично тому, как перераспределяются электроны в процессе обычной химической реакции.)
Предположим, вначале у нас было ядро атома азота (7 протонов, 7 нейтронов). Добавим сюда альфа-частицу (2 протона, 2 нейрона) и вычтем протон, который был «выбит» альфа-частицей. Получаем атом, состоящий из 8 протонов и 9 нейтронов, то есть кислород–17. В записи это выглядит так:
7N14 + 2Не4 → 1Н1 + 8О17, (Уравнение 9.1)
где подстрочный индекс — атомные числа, а надстрочный — массовые. 2He4 — это ядро атома гелия, или альфа-частица, а 1H1 — ядро атома водорода, или протон. Обратите внимание, что сумма атомных чисел и правой, и левой частей формулы равняется 9, а массовых чисел — 18. Согласно законам сохранения электрического заряда и массы, при любых ядерных реакциях суммы атомных и массовых чисел исходных и образующихся продуктов должны быть равны.
Физики разработали и более короткий способ записи формул ядерных реакций. Так как по названию элемента можно узнать его атомное число, в формуле его просто не пишут. Символом альфа-частицы является α, а протона — p. Таким образом, формулу 9.1 можно представить как: N14 (α, p)O17.
По этой системе в левой части записывается ядро-мишень, затем в круглых скобках название ударяющей по нему частицы, потом — выбиваемой частицы. В правой части записывается остаточное ядро. Все семейство (α, p)-реакций можно представить в виде аналогичной формулы: в любой из таких реакций атомное число остаточного ядра будет на 1, а массовое — на 3 выше, чем у ядра-мишени.
Резерфорд провел и другие (α, p)-реакиии, однако встретился с серьезными ограничениями. Дело в том, что и альфа-частица, и ядро-мишень обладают положительным зарядом и отталкивают друг друга. Чем выше атомное число ядра, тем сильнее они отталкиваются, и даже самым быстрым альфа-частицам радиоактивных элементов не хватает энергии, чтобы преодолеть силы отталкивания ядер элементов с зарядом выше калия (+19).
Нужно было найти способ получения субатомных частиц, энергия которых была бы выше, чем у радиоактивных частиц.
Электронвольт
Заряженную частицу можно ускорить, подвергнув ее действию электрического поля, направленного по ходу движения частицы. Чем выше потенциал этого электрического поля, тем выше ускорение и энергия частицы.
Частица с единичным зарядом, например электрон, под действием электрического поля напряжением 1 вольт получает заряд энергии, равный 1 электронвольту (сокращенно эв). 1 эв равен 1,6∙10–12. Для более крупных зарядов используется килоэлектронвольт (Кэв). 1 Кэв равняется 1000 эв.
Существуют также мегаэлектронвольт (Мэв), равный миллиону электронвольт, и биллион электронвольт (Бэв)[134]. Биллион электронвольт равняется 1,6∙10–8. В принципе это очень небольшое количество энергии, но для одной субатомной частицы оно просто огромно.
В последнее время в электронвольтах все чаще обозначают массу субатомных частиц. Масса электрона равна 9,1∙10–28 граммов. По формуле Эйнштейна e = mc2 (см. ч. II) получаем энергетический эквивалент, равный 8,2∙10–7 эрг, что, в свою очередь, равно 510 000 эв, или 0,51 Мэв.
Длину волны электромагнитного излучения также можно представить в электронвольтах. Согласно квантовой теории, e = hν, где e — энергия одного кванта электромагнитного излучения, эрг; h — постоянная Планка, эрг/сек, ν — частота излучения, Гц.
Таким образом, длина волны (обозначается λ, — «лямбда») равняется пройденному излучением за одну секунду в вакууме расстоянию (c), деленному на количество образовавшихся за это время волн, то есть частоту излучения ν:
λ = c/ν (Уравнение 9.2)
или
ν = c/λ. (Уравнение 9.3)
Поставив c/λ в формулу квантовой теории e = hν , получим:
e = hc/λ (Уравнение 9.4)
или
λ = hc/e, (Уравнение 9.5)
где h равняется 6,62∙10–27 эрг-с, а c — 3,00∙1010 см в секунду, соответственно hc равняется 1,99∙10–16 эрг. Приводим уравнение 9.5 к виду:
l = 1,99∙10–16/e. (Уравнение 9.6)
Теперь, если мы подставим 1,6∙10–12 эрг (один электрон вольт) вместо e в формуле 9.6, то получим 1,24∙10–4 сантиметров. Другими словами, излучение длиной 1,24 микрона (инфракрасный спектр) состоит из протонов, энергия которых 1 эв.
Таким образом, 1 Кэв — это энергия излучения, длина волны которого в 1000 раз больше 1 эв, т. е. 1,24 миллимикрона, или 12,4 ангстрема. Это уже диапазон рентгеновского излучения. Точно так же 1 Мэв — это энергия излучения, длина волны которого 0,0124 ангстрема (диапазон гамма-лучей).
По формуле 9.6, запас энергии видимого света колеблется от 1,6 эв для красной части спектра и 3,2 эв для фиолетовой. Видимый свет и ультрафиолетовое излучение поглощаются и испускаются во время обычных химических реакций. Таким образом, во время обычных химических реакций используется энергия не более 1–5 эв. Основная сложность проведения ядерных реакций заключается в том, что для таких реакций энергии нужно гораздо больше — тысячи, даже миллионы электронвольт.
Ускорители частиц
Устройства, испускающие субатомные частицы с уровнем энергии в несколько килоэлектронвольт и выше, получили названия ускорителей элементарных частиц. Так как такие частицы используются для разрушения атомных ядер и возбуждения ядерных реакций, то устройства также называли ускорителями ядерных частиц, но сейчас этот термин практически вышел из моды.
Первый удачный ускоритель частиц, адаптированный под ускорение протонов, был сконструирован английским физиком Джоном Кокрофтом (1897–1967) и его ирландским коллегой Эрнестом Уолтоном (1903–1995) в 1929 году.
Протоны в ядерных реакциях использовать удобнее, чем альфа-частицы, так как они обладают меньшим зарядом и поэтому меньше подвержены силам отталкивания ядра.
Кроме того, протоны являются ионизированными атомами водорода (Н+), в то время как альфа-частицы являются ионизированными атомами гелия (Не++), а водород гораздо легче ионизируется.
В ускорителе Кокрофта — Уолтона для получения огромного электрического, заряда и ускорения протонов до 380 Кэв применялся умножитель напряжения (связка из нескольких конденсаторов).
В 1931 году ученые смогли настолько ускорить частицы, что им удалось разрушить ядро атома лития:
3Li7 + 1H1 → 2He4 + 2He4. (Уравнение 9.7)
Это была первая полностью искусственная реакция, так как даже применявшиеся при ее проведении бомбардирующие частицы были получены искусственно.
В том же 1931 году были созданы еще три типа ускорителей частиц.
Американский физик Роберт Ван-де-Грааф (1901–1967) построил механизм, внешне напоминавший половину гантели, поставленную на пол. Внутри находился «конвейер», переносивший положительный заряд в верхнюю часть, а отрицательный — в нижнюю, создавая огромный разноименный электростатический заряд. Благодаря значительной разности потенциалов с помощью такого электростатического генератора можно было разгонять частицы до 1,5 Мэв, а впоследствии и до 18 Мэв.
Ускорители последующего типа состояли из нескольких раздельных труб. Такое устройство давало возможность «толкать» частицы в несколько приемов, а не одним мощным «пинком». Проходя по трубе, частица получала дополнительную энергию и скорость. Так как «толчки» осуществлялись через одинаковые периоды времени, то расстояние, которое частица проходила между «толчками», становилось все больше и больше, и каждая последующая труба должна была быть все длиннее и длиннее. Поэтому очень скоро линейный ускоритель стал слишком длинным и неудобным.
Эрнест Орландо Лоуренс (1901–1958) предложил схему самого компактного ускорителя. В его устройстве частицы перемещались не по прямой, а по кривой траектории, благодаря чему и удалось сэкономить место.
В центре закрытого плоского круглого сосуда помещается высокотемпературная спираль, ионизирующая водород для образования протонов. Противоположные части сосуда находятся под высоким напряжением, которое и ускоряет протоны. Находящиеся над и под сосудом магниты заставляют протоны двигаться по криволинейной траектории.
Двигающиеся по такой криволинейной траектории протоны в конце концов попадут в зону положительного заряда и начнут тормозиться. Однако сосуд находится под переменным током, и анод с катодом «меняются местами» с тщательно подобранной частотой.
Всякий раз, когда протоны, казалось бы, двигаются к аноду, тот становится катодом и протоны продолжают ускоряться. (Как будто борзая гонится за электрическим кроликом, который всегда остается впереди.)
По мере ускорения скорость протонов растет, и они делают обороты внутри сосуда все быстрее и быстрее. А часть переменного электрического поля остается прежней постоянной величиной. Происходит рассинхронизация, и протоны окажутся под действием отталкивающей силы анода, который не успел вовремя стать катодом, что приведет к торможению протонов. (Борзая прибавила скорости и догнала электрического зайца.)
К счастью, по мере ускорения траектория протонов под действием магнитного поля становится менее криволинейной, и они начинают описывать большие круги. Их большая скорость просто-напросто компенсируется большим расстоянием, которое они проходят. Поэтому они продолжают передвигаться из одной половины в другую в соответствии с частотой электрического тока, постепенно все больше и больше удаляясь от центра сосуда. В конце концов они вылетают из него 9 виде потока частиц большой энергии.
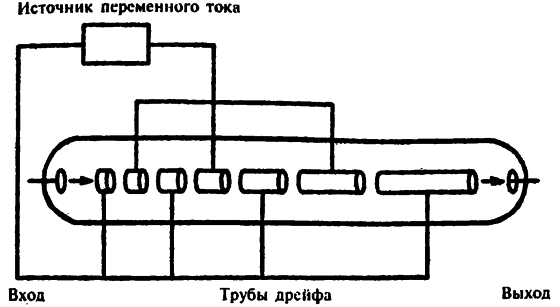
Линейный ускоритель частиц
Лоуренс назвал свой ускоритель циклотроном. Даже самая первая тестовая модель циклотрона — не более 25 сантиметров в диаметре — позволяла ускорять частицы до 80 Кэв. На протяжении последующих 10 лет строились все более крупные циклотроны, позволявшие ускорять частицы до 10 Мэв и более.
Идеального соответствия между движением частицы и частотой электрического тока можно добиться только при условии, что масса частицы не меняется. Это удается при нормальных условиях, однако в процессе ускорения скорость движения частиц начинает приближаться к скорости света. Согласно теории относительности (см. ч. II), в этом случае скорость частицы начинает расти очень и очень медленно (скорость движения частицы ни в коем случае не может быть выше скорости света), в то время как рост массы частицы все ускоряется и ускоряется.
Чем больше масса частицы, тем больше времени она затрачивает на один полуоборот и синхронизацию между движением частицы и частотой переменного тока. Это ограничивает максимальную скорость ускорения протона, и еще до Второй мировой войны эта максимальная скорость была достигнута.
В 1945 году американский физик Эдвин Макмиллан (1907–1991) и русский физик Владимир Векслер независимо друг от друга предложили способ обойти это ограничение. Ученые показали, как именно частоту переменного тока можно постепенно понижать без рассинхронизации с движением частицы постоянно увеличивающейся массы. В результате был построен синхроциклотрон.
Синхроциклотрон не способен испускать частицы высокой энергии беспрерывно, так как частота переменного тока, приемлемая для частиц на последних стадиях ускорения, слишком низкая для частиц на начальных стадиях. Поэтому частицы ускоряются пакетами (по 60–300 частиц) в секунду: перед запуском нового пакета предыдущий должен пройти весь цикл. Однако значительное увеличение скорости частиц на выходе привело к сокращению их общего количества. Первый синхроциклотрон был построен в 1946 году, а несколькими годами позднее появились синхроциклотроны, позволяющие ускорять частицы до 800 Мэв.
При ускорении электронов проблема увеличения релятивистской массы появляется еще раньше. Электроны настолько легкие, что для придания хотя бы умеренного заряда их необходимо разогнать до очень высоких скоростей. Чтобы получить электрон с энергией всего лишь 1 Мэв, его нужно разогнать до 270 000 км/с, а это уже более 9/10 скорости света.
При такой скорости масса электрона увеличивается в 2,5 раза по сравнению с состоянием покоя. Поэтому нет особого смысла разгонять электрон с помощью циклотрона, так как даже при небольших уровнях энергии электрона синхронизация уже будет невозможна.
Решение было найдено еще до появления синхроциклотрона. В 1940 году американский физик Дональд Керст разработал ускоритель, в котором электроны двигались по «бубликообразному» сосуду. С ростом скорости движения электронов увеличивалась интенсивность магнитного поля, заставляющего электроны двигаться по кругу. Так как увеличение интенсивности магнитного поля (заставляет электроны двигаться по меньшему радиусу) было согласовано с ростом массы электрона (заставляет электроны двигаться по большему радиусу), в конечном результате электроны не меняют свою траекторию. В определенный момент интенсивность магнитного поля резко изменяют, и несколько электронов высокой энергии вылетают из ускорителя. Керст назвал свой ускоритель бетатроном, так как бета-частицы являются электронами высокой энергии естественного происхождения. Ускоритель Керста испускал электроны с энергией до 2,5 Мэв, а самый современный бетатрон позволяет ускорять электроны до 340 Мэв.
Быстро движущиеся по орбитам электроны испытывают сильное центростремительное ускорение и согласно теории Максвелла испускают энергию в виде излучения. Это ограничивает максимальное ускорение электронов в любом устройстве, где электроны движутся по кругу. (Протоны менее подвержены этому явлению, так как при одинаковом уровне энергии скорость движения протонов существенно ниже, чем у электронов, а значит, и центростремительное ускорение у них гораздо ниже.)
Поэтому сейчас принимаются усилия по строительству линейных ускорителей с длиной, достаточной (сейчас планируется строительство 3,5-километрового ускорителя) для ускорения электронов до 20 000 Мэв.
У синхроциклотрона есть один практический недостаток. Во время движения от центра к выходу частица описывает круги все большего и большего радиуса, поэтому необходимо использовать магниты, достаточные для покрытия максимального радиуса. Эти огромные магниты как раз и были узким местом при строительстве больших синхроциклотронов.
Поэтому целесообразнее было подстраивать интенсивность магнитного поля так, чтобы протоны двигались по кругу, а не по спирали. При такой «жесткой фокусировке» протоны двигаются максимально плотным и узким лучом. Построенные по такому принципу устройства получили названия протонные (и электронные) синхротроны.
К 1952 году были построены протонные синхротроны, способные разгонять частицы до нескольких Бэв. Такой синхротрон, способный испускать частицы с уровнем энергии до 6,2 Бэв, есть у университета штата Калифорния, и называется он бэватрон,
В 1960-х годах были построены два огромных ускорители с жесткой фокусировкой (один в Женеве, второй в Брукхейвене, Лонг-Айленд). Эти ускорители способны разгонять протоны до 30 Бэв и выше. Планируется построить и еще большие, поистине колоссальные по размерам ускорители. Самые большие из существующих ускорителей равны в диаметре трем городским кварталам.
Глава 10.
Дата: 2019-07-24, просмотров: 335.