Электрические цепи, предназначенные для выделения колебаний, лежащих в определенном диапазоне частот, называются электрическими фильтрами.

Электрический фильтр представляет собой четырехполюсник, пропускающий без заметного ослабления колебания определенных частот и с большим ослаблением колебания других частот. Полоса частот, в которой затухание фильтра мало, – полоса пропускания (прозрачности). Остальная область частот – полоса задерживания (подавления). Классификация электрических фильтров проводится по различным признакам.

1. Классификация по расположению полосы (полос) пропускания:

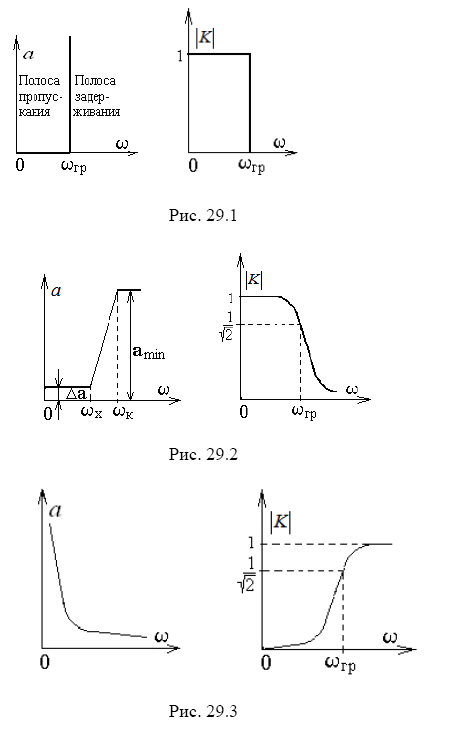
Фильтры нижних частот – полоса пропускания от f=0 до f-граничная. На рис. 29.1 изображены амплитудно-частотные характеристики идеального фильтра нижних частот в координатах a(ω) и K, a(ω) – затухание, K – модуль передаточной функции по напряжению. В реальном фильтре достичь таких характеристик невозможно. Поэтому при проектировании фильтра задается допустимое максимальное затухание в полосе пропускания и необходимое минимальное затухание в полосе задерживания. Между этими полосами находится промежуточная полоса – полоса перехода (рис. 29.2). В эффективной полосе пропускания от ω = 0 до частоты ωX задано допустимое максимальное затухание Δa, в полосе от частоты ωk до бесконечности – необходимое минимальное затухание amin. В полосе перехода от ωX до ωk затухание не задается;

если полоса пропускания находится в пределах от f-граничная до бесконечности, то такие фильтры называются фильтрами верхних частот (рис. 29.3);

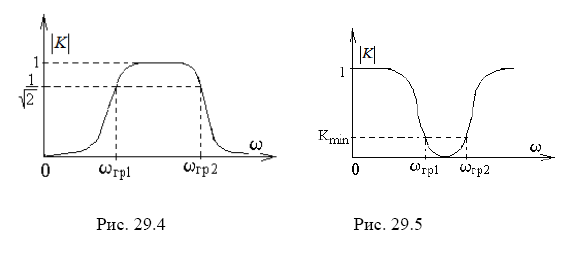
полосовые фильтры (рис. 29.4) имеют две частоты, ограничивающие полосу пропускания:

заграждающий, или режекторный, фильтр (ЗФ, РФ) имеет вместо полосы пропускания полосу режекции с граничными частотами 0 < ωгр1 < ωгр2 < ∞, которые определяются на заданном минимальном уровне Kmin (рис. 29.5);

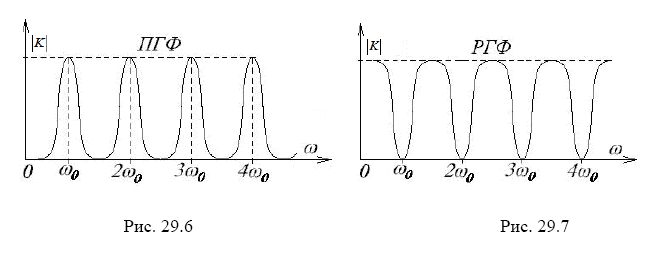
при приёме радиолокационных и других импульсных сигналов используются фильтры, имеющие ряд одинаковых полос пропускания – полосовые гребенчатые фильтры (ПГФ) с кратными средними частотами полос пропускания (рис. 29.6);

гребенчатые фильтры, имеющие дискретный ряд полос режекции, называются заграждающими или режекторными гребенчатыми фильтрами (ЗГФ, РГФ), рис. 29.7.

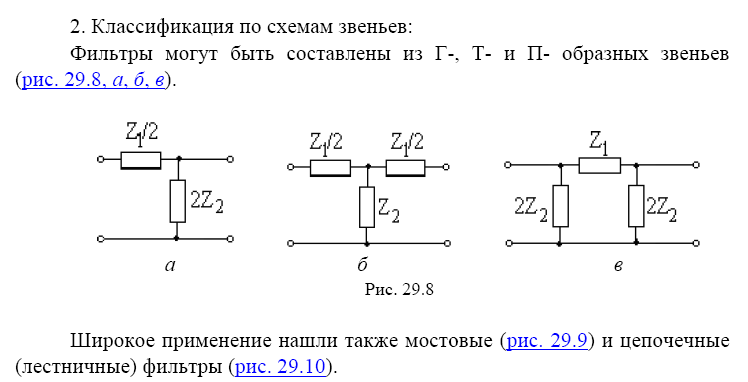
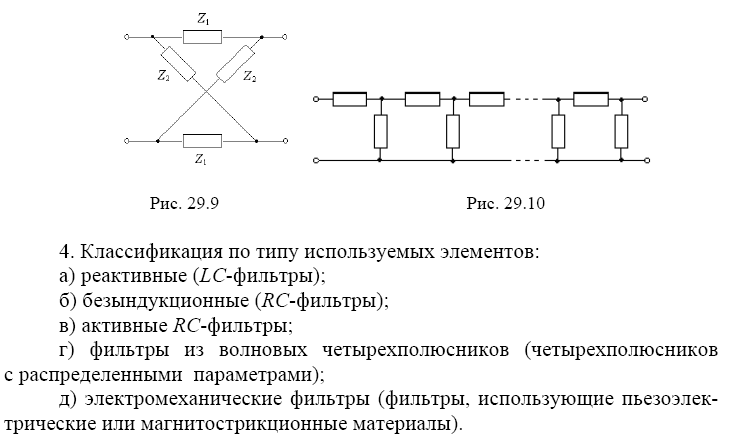
3. Классификация по типу используемых элементов:

реактивные (LC-фильтры)

безындуктивные (RC-фильтры)

активные RC-фильтры

фильтры из волновых четырехполюсников (четырехполюсников с распределенными параметрами)

электромеханические фильтры (фильтры, использующие пьезоэлектрические или магнитострикициооные материалы)

4. Классификация фильтров по типам характеристик:

1. фильтры типа k (простейшие Г-, Т-, П-образные фильтры)

2. фильтры типа m (производные фильтры более высокого порядка)

Физическое действие фильтров объясняется тем, что на низких частотах сопротивления индуктивностей малы, а сопротивления емкостей велики; на высоких же частотах наоборот: сопротивления индуктивностей велики, а емкостей – малы.

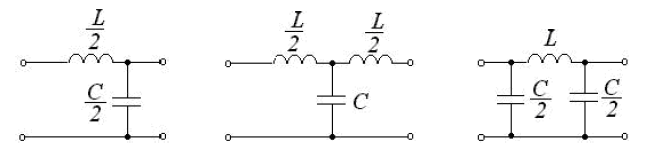
Варианты реализации ФНЧ и их АЧХ и ФЧХ представлены на рисунках ниже:

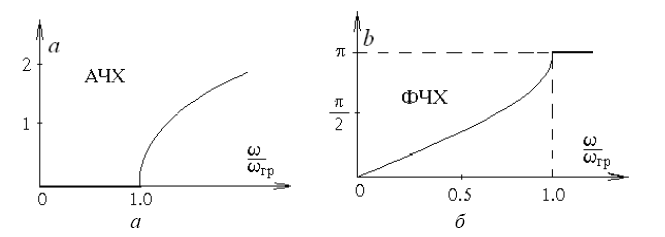
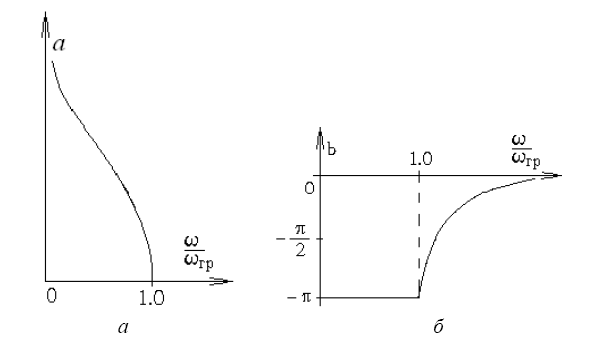
Фильтры верхних частот. Фильтром верхних частот называют четырехполюсник, у которого затухание в диапазоне от ω=0 до граничной частоты ω_гр велико, а в диапазоне от ω_гр до ω=∞ мало. Определим полосу пропускания фильтров верхних частот.

Графики АЧХ и ФЧХ для ФВЧ представлены ниже:

Полосовые фильтры. Для повышения избирательности вместо колебательных контуров используются полосовые фильтры, представляющие собой два связанных контура, сопротивление связи между которыми резко изменяется с частотой, что приводит к значительному улучшению частотных характеристик. Полосовые фильтры (рис. 30.8) имеют в продольной ветви резонанс напряжений на частоте ω0, а в поперечной – резонанс токов; причем резонансные частоты последовательного и параллельного контуров одинаковы.

Рассмотрим работу полосового (например, Т-образного) фильтра при холостом ходе. На частоте ω0 оба последовательных контура являются коротким замыканием, а параллельный контур имеет бесконечно большое сопротивление (рис. 30.9, а).

Напряжение на выходе фильтра равно входному напряжению, т. е. a = 0 (|К_ХХ| = 1). На частотах ω > ω₀ последовательные контуры имеют индуктивное сопротивление, а параллельный – емкостное сопротивление (рис. 30.9, б). Следовательно, эквивалентная схема полосового фильтра представляет собой фильтр нижних частот, имеющий полосу пропускания от ω = 0 до некоторой граничной частоты ω = ω_B. На частотах ниже резонансной частоты ω < ω₀ последовательные контуры имеют емкостное сопротивление, а параллельный – индуктивное сопротивление. Из эквивалентной схемы (рис. 30.9, в) видно, что она является фильтром верхних частот, в полосе пропускания которого от ω_H до ω = ∞, а = 0.

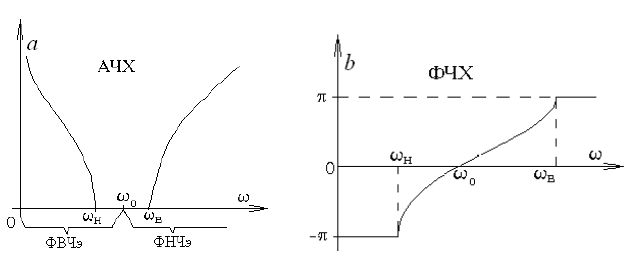
Графики АЧХ и ФЧХ для полосовых фильтров:

Заграждающие фильтры. Заграждающие фильтры (рис. 30.15) можно получить, поменяв в полосовых фильтрах местами последовательный и параллельный контуры.

При частоте ω = ω0 продольная ветвь окажется разомкнутой, а поперечная – замкнутой накоротко (рис. 30.16, а), т. е. затухание фильтра бесконечно велико.

На частотах ω > ω0 последовательная ветвь становится емкостным сопротивлением, а параллельная – индуктивным сопротивлением, т. е. схема обращается в фильтр верхних частот (рис. 30.16, б), пропускающий частоты выше граничной частоты ω_B.

Наконец, при частотах, меньших ω0, последовательная ветвь приобретает характер индуктивного сопротивления, а параллельная – емкостного сопротивления.

В этом случае цепь выполняет роль фильтра нижних частот (рис. 30.16, в), пропускающего без ослабления частоты ниже граничной.

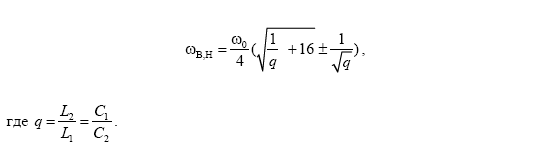
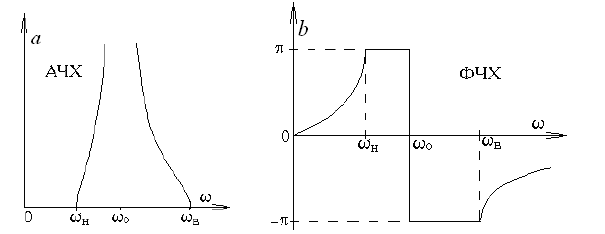
Графики АЧХ и ФЧХ для заграждающего фильтра:

Электроника