Это сложный, но нужный этап. Назначение этого этапа – установить, правильно ли понята задача, не противоречит ли полученный ответ всем другим условиям задачи, т.е. учит самоконтролю. Этот этап является обязательным при решении задачи.

 Существуют разные способы проверки:

• Прикидка
• Решение обратных задач, наиболее эффективный способ самоконтроля.
• Установление соответствия между данными и искомым
• Сравнение с правильным ходом решения
• Решение другим способом.

Последнему способу проверки необходимо уделять как можно больше внимания.

Постоянная работа в этом направлении очень важна и для развития ребёнка, и для формирования умения решать задачи. Это увлекательное и полезное дело для учащихся начальных классов. Оно осуществляет право ученика на выбор решения (даже если оно не является традиционным), у него появляется дополнительная возможность самореализации. Когда есть выбор при решении задачи, встаёт вопрос о нахождении рационального пути решения.

Если проверка показывает, что задача решена верно, дети записывают  ответ задачи. Если проверка показывает, что задача решена неверно, возвращаются к первому этапу работы над задачей.

Компонент 7. Исследование задачи.

Исследование задачи начинается на этапе осмысления, но может быть продолжено и  дальше, если возникает необходимость преобразовать текст в задачу, дополнить или убрать лишнее. В полной мере исследовательской работой можно заняться после частичного или полного решения задачи. Это может быть

- установление зависимости между изменением одного элемента задачи и изменением её решения

- сравнение задач сходных по фабуле, но разных по математическому содержанию или с одинаковым математическим содержанием, но внешне совершенно непохожих друг на друга.

- классификация задач по выбранным признакам

Исследовательская работа помогает разнообразить деятельность детей на уроке, поддерживает интерес к математике, помогает лучше понять и усвоить   взаимосвязи между величинами, т.е. способствует формированию  компетентностного подхода.

ИПМ 4  Вывод

Такая работа, которая проводится в системе, способствует развитию учебной мотивации, большинству детей помогает видеть взаимосвязь между величинами, овладевать разными способами решения задач, т.е. способствует формированию математической компетентности.

Исследовательская деятельность помогает разнообразить деятельность детей на уроке, поддерживает интерес к математике и, главное, помогает им овладеть умением решать задачи. Конечно, подобный вид работы, требует больших затрат времени. Однако время, потраченное на них, окупается умением решать задачи не только на уровне государственных стандартов, но и нестандартные задачи. А самое главное у детей появляется желание решать задачи.

Это подтверждает диагностика, проведённая в 4 «Б» классе МОУ «ОСОШ №1» . Отвечали 25 детей. ( Результативность для детей.)

1. Нравится ли тебе урок математики?

Да – 64% Не очень – 32% Нет – 4% (1 человек)

2. Любишь ли ты решать задачи?

Да – 60% Не очень – 24% Нет - 16%

3. Пытаешься ли ты самостоятельно решать задачи несколькими способами?

Да – 48% Иногда – 24%    Нет – 28%

4. Зачем нужно уметь решать задачи несколькими способами?

Ø Чтобы быть умным - 10 человек;

Ø Чтобы получать пятёрки - 2 человека;

Ø Для образования, чтобы поступить в институт - 1 человек;

Ø Поможет в жизни -1 человек;

Ø Пригодится в будущем - 3 человека;

Ø Для развития логики, умственных способностей - 3 человека;

Ø Так интереснее и труднее - 2 человека;

Ø Очень хочется узнать, как можно решить по-другому - 2 человека;

Ø Не знаю – 1 человек.

Результативность для учителя (на примере 4 «Б» класса, программа «Начальная школа ХХI века», автор Виноградова Н.Ф.). 1кл.- входная диагностика, 2-4 классы по итогам контрольных работ.

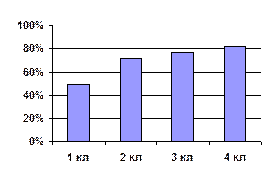
Но, если детям дать достаточно времени, что и предусматривает компетентностный подход, то практически все  смогут решить задачи (на уровень государственного стандарта).

Возможность использования

Решение задач по алгоритму может успешно применяться во всех программах начальной школы.

Библиография

1. Аргинская И.И., Дмитриева Н.Я.Обучаем по системе Л.В. Занкова: 2кл.: Кн. Для учителя. – М.: Просвещение, 1993. – 160с.
2. Занков Л.В. Беседы с учителями. (Вопросы обучения в начальных классах.) М., Просвещение, 1970. - 200с.
3. Иванов Д.А., Митрофанов К. Г., Соколова О.В. Компетентностный подход в образовании. Проблемы, понятия, инструментарий. М.: изд-во Академии повышения квалификации и проф. переподготовки работников образования.- 2006г.
4. Лысенкова. С. Н.. Когда легко учиться: из опыта работы учителя начальных классов школы №587 Москвы.- 2-е изд.М.: Педагогика, 1985 – 176с.(пед. поиск: опыт, проблемы, находки)
5. Мамыкина М. Ю. Работа над задачей в системе Л. В. Занкова. Начальная школа

№ 4.2003г.

1. Матвеева Н.А.. Различные арифметические способы решения задач. Начальная школа №3.2001г.
2. Математика. 1-4 классы: обучение решению текстовых задач/ авт.-сост. И.Л. Кустова. – Волгоград: Учитель, 2009. – 103с.
3. Новиков А.Учебный процесс в логике исторических типов организационной культуры. Народное образование №1, 2008г.с.163
4. Петерсон Л.Г., Кубышева М.А., Мазурина С.Е., Зайцева И.В. Что значит «уметь учиться». – М.: АПК и ППРО, УМЦ «Школа 2000…», 2008. – 80с.
5. Узорова, Нефёдова. 500 задач с пояснением, пошаговым решением и правильным оформлением. 1класс. АСТ.: Астрель. Москва.2004г.
6. Фадеева. Схемы записи задач. Начальная школа №4.2003г.
7. Фонин С.Н.. Моделирование, как важное средство обучения решению задач. Начальная школа. №3.1990г.
8. Шульга Р.П. Решение задач разными способами – средство повышения интереса к математике. Начальная школа №12. 1990г.

Приложение 1