Экспериментальная работа проводилась в 8 классе в три этапа.
Первый этап
Проведение диагностической самостоятельной работы № 1.
На самостоятельной работе ученикам было предложено 3 задания, которые было необходимо выполнить в течение 5 мин. [Прил.1]
Количество детей, участвующих в исследовании: 20.
Результаты диагностирующей самостоятельной работы № 1 отражены в таблице 1.
Таб. 1
| № | Количество детей, которые решили задание |
| 1 | 8 |
| 2 | 6 |
| 3 | 11 |
На основании начальной самостоятельной работы были составлены группы из 10 человек (Группы были сформированы следующим способом: 4 человека, показавшие средние результаты, 4 человека, показавшие низкие результаты, 2 человека, показавшие высокий результат при решении задач)
Второй этап
Проведение занятий с внедрением дифференциальных подходов.
Занятия проводились 1 раз в неделю по 2 ч. Всего было проведено 2 занятия. [Прил.2,3]
Основные задачи проведения занятий:
1) выявить тот материал, который вызывает у учащихся наибольшие трудности;
2) определить эффективность усвоения материала с помощью текущей проверки;
3) выявить заинтересованность учащихся в изучении данной темы. Работа в группах позволила ученикам оказывать взаимную помощь друг другу в процессе обучения, кроме того, при помощи самостоятельной работы я ориентировалась в своем подходе к преподаванию материала детям разных категорий.
Третий этап
Проведение диагностирующей самостоятельной работы № 2.
Самостоятельная работа была проведена после проведения дифференционных занятий.
Задача: выявление знаний и умений решать задачи на тему «Действительные числа».
Ученикам было предложено 3 задания, которые было необходимо выполнить в течение 5 мин. [Прил.4]
Результаты диагностирующей самостоятельной работы № 2 отражены в таблице 2.
Таб. 2
| № | Количество учеников, которые решили задания |
| 1 | 14 |
| 2 | 11 |
| 3 | 17 |
На основании данных, приведенных в таблицах можно сделать заключение об эффективности дифференциального метода в преподавании математики для повышения успеваемости учеников 8 класса.
2.4. Система упражнений для подготовки к ОГЭ учащихся 9 классов по теме «Действительные числа»
Опираясь на требования к системе упражнений В.А. Байдака [18] и кодификатор элементов содержания и требований к уровню подготовки обучающихся для проведения ОГЭ по математике была создана следующая система упражнений, которая включает в себя 2 задания, связанных с действительными числами.
Числа и вычисления
Пример 1. Сколько целых чисел расположено между числами 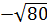 и
и 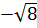 [19]?
[19]?
Решение:
1) 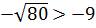
2) 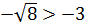
3) тогда получаем: 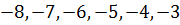
Ответ: 6.
Пример 2. Какое из чисел отмечено на координатной прямой точкой 𝐴 [19]?
A x
0 1 2 3 4
1) 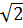 ; 2)
; 2) 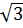 ; 2)
; 2) 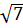 ; 2)
; 2) 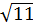 .
.
Решение: Возведем в квадрат числа 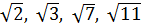 :
:
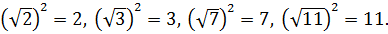
Число 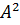 лежит между числами
лежит между числами 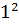 = 1 и
= 1 и 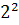 = 4 и ближе к числу
= 4 и ближе к числу 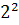 . Поэтому точкой A отмечено число
. Поэтому точкой A отмечено число 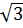 .
.
Ответ: 2.
Пример 3. Одна из точек, отмеченных на координатной прямой, соответствует числу 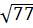 . Какая это точка [19]?
. Какая это точка [19]?
A B C D x
7 8 9
1) точка A; 2) точка B; 3) точка C; 4) точка D.
Решение:
Возведем в квадрат числа 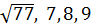 :
:
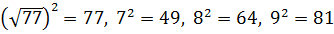 .
.
Число 77 лежит между числами 64 и 81 и находится ближе к числу 81, поэтому 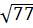 соответствует точке D.
соответствует точке D.
Ответ: 4.
Задания:
1. Сколько целых чисел расположено между числами 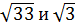 ?
?
2. Сколько целых чисел расположено между числами 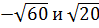 ?
?
3. Сколько целых чисел расположено между числами 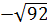 и
и 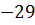 ?
?
4. Сколько целых чисел расположено между числами 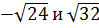 ?
?
5. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 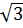 ; 2)
; 2) 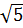 ; 3)
; 3) 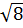 ; 4)
; 4) 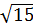 .
.
6. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 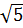 ; 2)
; 2) 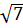 ; 3)
; 3) 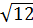 ; 4)
; 4) 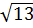 .
.
7. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 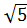 ; 2)
; 2) 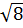 ; 3)
; 3) 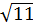 ; 4)
; 4) 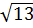 .
.
8. Одна из точек, отмеченных на координатной прямой, соответствует числу 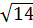 . Какая это точка?
. Какая это точка?
M N P Q x
3 4 5
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
9. Одна из точек, отмеченных на координатной прямой, соответствует числу 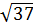 . Какая это точка?
. Какая это точка?
M N P Q x
5 6 7
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
10. Одна из точек, отмеченных на координатной прямой, соответствует числу 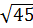 . Какая это точка?
. Какая это точка?
M N P Q
6 7 8
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
Алгебраические выражения
Пример 1. Укажите наибольшее из следующих чисел [19]:
1) 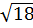 ; 2)
; 2) 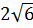 ; 3) 5; 4)
; 3) 5; 4) 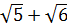 .
.
Решение: Возведем в квадрат числа 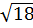 ;
; 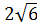 ; 5;
; 5; 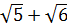 :
:
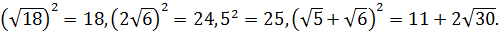
Поскольку 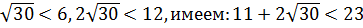 .
.
Таким образом, наибольшее число 5.
Ответ: 3.
Пример 2. Расположите в порядке возрастания числа 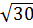 ;
; 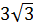 ; 5,5 [19].
; 5,5 [19].
1) 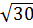 ;
; 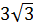 ; 5,5; 2) 5,5;
; 5,5; 2) 5,5; 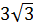 ;
; 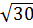 ; 3)
; 3) 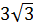 ; 5,5;
; 5,5; 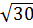 ; 4)
; 4) 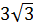 ;
; 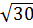 ; 5,5.
; 5,5.
Решение: Возведем каждое из чисел в квадрат:
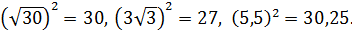
Сравним квадраты заданных чисел: 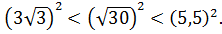
Следовательно, 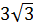 ;
; 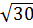 ; 5,5.
; 5,5.
Ответ: 4.
Пример 3. Найдите значение выражения 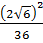 [19].
[19].
1)  ; 2)
; 2)  ; 3) 2; 4) 4.
; 3) 2; 4) 4.
Решение: Последовательно получаем:
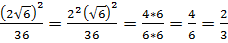 .
.
Ответ: 1.
Задания:
1. Укажите наибольшее из следующих чисел:
1) 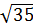 ; 2)
; 2) 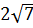 ; 3) 6; 4)
; 3) 6; 4) 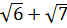 .
.
2. Укажите наименьшее из следующих чисел:
1) 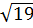 ; 2)
; 2) 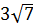 ; 3) 6; 4)
; 3) 6; 4) 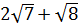 .
.
3. Укажите наибольшее из следующих чисел:
1) 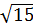 ; 2)
; 2) 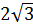 ; 3) 3; 4)
; 3) 3; 4) 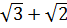 .
.
4. Укажите наименьшее из следующих чисел:
1) 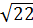 ; 2)
; 2) 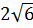 ; 3)
; 3) 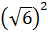 ; 4)
; 4) 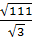 .
.
5. Расположите в порядке возрастания числа 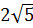 ;
; 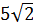 ; 6.
; 6.
1) 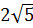 ;
; 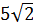 ; 6; 2)
; 6; 2) 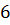 ;
; 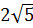 ;
; 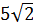 ; 3)
; 3) 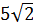 ; 6;
; 6; 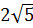 ; 4)
; 4) 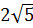 ; 6;
; 6; 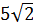 .
.
6. Расположите в порядке возрастания числа 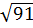 ; 9,5;
; 9,5; 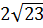 .
.
1) 9,5; 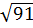 ;
; 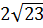 ; 2)
; 2) 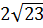 ;
; 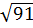 ; 9,5; 3) 9,5;
; 9,5; 3) 9,5; 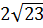 ;
; 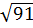 ; 4)
; 4) 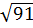 ; 9,5;
; 9,5; 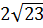 .
.
7. Расположите в порядке возрастания числа 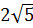 ;
; 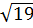 ; 4,5.
; 4,5.
1) 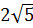 ;
; 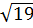 ; 4,5; 2)
; 4,5; 2) 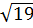 ; 4,5;
; 4,5; 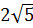 ; 3)
; 3) 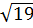 ;
; 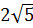 ; 4,5; 4) 4,5;
; 4,5; 4) 4,5; 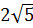 ;
; 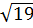 .
.
8. Расположите в порядке возрастания числа 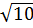 ;
; 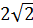 ; 3,5.
; 3,5.
1) 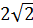 ; 3,5;
; 3,5; 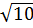 ; 2) 3,5;
; 2) 3,5; 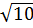 ;
; 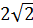 ; 3)
; 3) 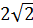 ;
; 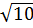 ; 3,5; 4)
; 3,5; 4) 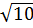 ;
; 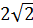 ; 3,5.
; 3,5.
9. Найдите значение выражения  .
.
1)  ; 2) 3; 3)
; 2) 3; 3)  ; 4)
; 4)  .
.
10. Найдите значение выражения 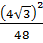 .
.
1)  ; 2) 27; 3)
; 2) 27; 3) 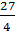 ; 4) 1.
; 4) 1.
11) Найдите значение выражения 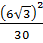 .
.
1)  ; 2)
; 2) 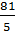 ; 3)
; 3) 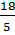 ; 4)
; 4) 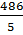 .
.
12. Найдите значение выражения 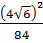 .
.
1) 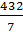 ; 2)
; 2)  ; 3)
; 3) 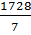 ; 4)
; 4)  .
.
ПРИЛОЖЕНИЯ
1.2.3.4.
ЗАКЛЮЧЕНИЕ
Успех проводимой в нашей стране модернизации образования во многом зависит от правильного определения роли и места каждого школьного предмета в новых, быстро меняющихся условиях. При этом определены приоритетные направления развития школы, такие как гуманизация, гуманитаризация, ориентированные на формирование личности школьников, реализацию их задатков, склонностей, способностей, интересов и других индивидуальных особенностей. В этом большую роль играет школьный курс математики.
Современная тенденция в раскрытии сущности дифференциации обучения состоит в том, что дифференциацию обучения понимают как систему, которая лежит в основе учебно-воспитательного процесса (то есть является организационно-методическим принципом построения школы) и направлена на реализацию индивидуального подхода в обучении.
Внедрение в практику учебно-воспитательной работы принципа индивидуального подхода требует разработки системы воздействия на ученика с учетом его индивидуальных и возрастных возможностей, то есть внедрение дифференциации обучения.
Опыт внедрения дифференциального метода для преподавания темы «Действительные числа» показал свою эффективность, улучшено усвоение знаний, о чем свидетельствует повышение успеваемости класса.
ЛИТЕРАТУРА
1. Сухомлинский В.А. Избранные произведения: в 5 т. – Киев: Радянська школа, 1979, т1.
2. Унт И.Э. Индивидуализация и дифференциация обучения.- М.:Педагогика,1990.
3. Чередов И.М. Формы учебной работы в средней школе.- М.: Просвещение,1988.
4. Рабунский Е.С. Индивидуальный подход в процессе обучения школьников.- М.: Педагогика, 1975.
5. Чередов И.М. О дифференцированном обучении на уроках.- М.: Просвещение,1973.
6. Блонский П.П. о фуркации на втором концентре школы второй ступени
7. Андронов, И.К. Математика действительных и комплексных чисел [Текст]/ И.К.Андронов. – М.: Просвещение, 1975. – 158 с. Блок А.Я. Методика преподавания математики в средней школе: Частная методика: Учебное пособие для студентов пед. институтов по физ-мат спец. / А.Я. Блок, В.А. Гусев, Г.В. Дорофеев [и др.]; сост. В.И. Мишин. – М: Просвеще- ние, 1987
8. Александров, А.Д. Математика, ее содержание, методы и значение [Текст]/ Под ред. Александрова А.Д., Колмогорова А.Н., Лаврентьева М.А. – М.: Изд. Академии наук СССР, 2016.
9. Методика и технология обучения математике. Курс лекций: пособие для вузов[Текст]/ Под ред. Н.Л. Стефановой, Н.С. Подходовой. – М.: Дрофа, 2015.
10. Столяр, А.А. Логические проблемы преподавания математики [Текст]/ А.А. Столяр. – Минск: Высшая школа, 2015.
11. Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. - М .: Просвещение, 2016.
12. Аргунов Б.И., Балк М.Б. Элементарная геометрия. – М.: Просвещение, 2016.
13. Алфутова, А.Б. Алгебра и теория чисел для математических школ [Текст]/ А.Б. Алфутова, А.В. Устинов. – М.: МЦНМО, 2013.
14. Ключникова Е.М., Рабочая тетрадь по алгебре. 8 класс. К учебнику А.Г. Мордковича [Текст] / Е.М. Ключникова, И.В. Комиссарова. – М: Мнемозина, 2013.
15. Задачи по математике: алгебра и начала анализа [Текст]/ М.И. Башмаков, Б.М. Беккер, В.М. Гольховой. – М.: Высшая школа, 2004.
16. Байдак В.А. Теория и методика обучения математики: Учебное пособие [Текст] / В.А. Байдак. – М.: Флинта, 2011.
17. ОГЭ. 3000 задач с ответами по математике. Все задания части 1. Под. ред. Ященко И.В. М.: 2015.
Дата: 2019-04-22, просмотров: 688.