Одной из основных линий в школьном курсе математики является линия изучения чисел и действий над ними. В школе числовые множества изучают по следующей схеме:
«Схема изучения числовых множеств» [11]
| Действительные числа |
| Мнимые числа |
| Рациональные числа |
| Иррациональные числа |
| Целые числа |
| Дробные числа (положительные и отрицательные) |
| Отрицательные целые числа |
| Натуральные числа и ноль |
| Комплексные числа |
Из-за внутренних потребностей математики постепенно вводятся все новые для учеников числа. Столяровым А.А. была предложена следующая схема расширения числовых множеств [12]:
| Натуральные числа |
| Доли |
| Десятичные дроби |
| Отрицательные и целые числа |
| Рациональные числа |
| Иррациональные числа |
| Действительные числа |
Так, в младших классах для счета и сложения достаточно натуральных чисел. Умножение натуральных чисел тоже дает натуральное число. Если делимое кратно делителю, то и частное целое число. Как мы видим, операция деления имеет ограниченный характер в множестве N натуральных чисел: если 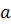 и
и 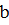 натуральные числа, то не всегда найдется натуральное число
натуральные числа, то не всегда найдется натуральное число 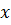 чтобы
чтобы  . Для того, чтобы устранить это несовершенство, в 5-6 классах вводятся дроби, записываемые в виде отношения
. Для того, чтобы устранить это несовершенство, в 5-6 классах вводятся дроби, записываемые в виде отношения 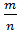 , где
, где 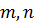 – натуральные числа. Дети начинают определять длину окружности, площадь круга, где используется число p (Пи), что приводит их к множеству рациональных чисел.
– натуральные числа. Дети начинают определять длину окружности, площадь круга, где используется число p (Пи), что приводит их к множеству рациональных чисел.
Так множество целых чисел Z расширяется до множества рациональных чисел следующим образом:
1. Определение рационального числа как дроби 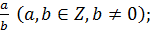
2. Определение равенства рациональных чисел ( 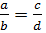 ⇔ 𝑎𝑑 = 𝑏𝑐, 𝑎,𝑐 ∈ 𝑍, 𝑏,𝑑 ∈ 𝑁);
⇔ 𝑎𝑑 = 𝑏𝑐, 𝑎,𝑐 ∈ 𝑍, 𝑏,𝑑 ∈ 𝑁);
3. Определение основных арифметических операций:
- суммы 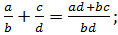
- произведения 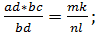
4. Свойства основных арифметических операций:
1) переместительный закон:
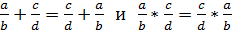 ;
;
2) сочетательный закон:
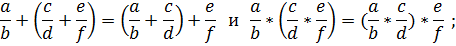
3) распределительный закон:
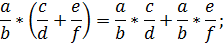
4) 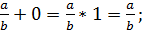
5) 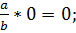
5. Определяются обратные арифметические операции сложению и умножению – вычитание и деление:
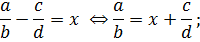
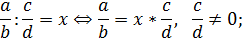
6. Определяется, как геометрически можно изобразить рациональное число;
7. Устанавливается связь между обыкновенной дробью и десятичной дробью (конечной и бесконечной периодической) – вводятся правила перехода от одних дробей к другим.[10]
В восьмом классе учащиеся вплотную знакомятся с иррациональными числами. Дети убеждаются в необходимости введения новых чисел при решении следующих задач:
§ решить уравнение: х2 = 2;
§ найти отношение длины дуги окружности к ее диаметру;
§ найти сторону квадрата, если его площадь 3 см2;
§ решить графически уравнение: х2 = 3;
§ к множеству каких чисел относятся числа 2, 31313…; 7,23233233…; 0, 123123412345…?
Перед изучением иррациональных чисел целесообразно обобщить знания о рациональных числах и действиях над ними.
Вспомнив все о множестве рациональных чисел, которое состоит из нуля, положительных и отрицательных целых чисел, положительных дробей и дробей, противоположных им, расширяем это множество до множества иррациональных чисел Q следующим образом:
1. В Q выполнима операция умножения 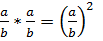 ∈ 𝑄;
∈ 𝑄;
2. Существует ли рациональное число, квадрат которого равен 2?
3. Определяется соизмеримость и несоизмеримость отрезков (геометрическое введение множества иррациональных чисел);
4. Дается определение иррациональных чисел как бесконечных десятичных непериодических дробей. [10]
Множество рациональных чисел расширяется до множества иррациональных чисел Q, а затем и до множества действительных чисел R. На основе сказанного, можно дать такую формулировку определению действительных чисел: совокупность рациональных и иррациональных чисел составляет множество действительных чисел.
Отметим, что основные положения, связанные с развитием у учащихся представлений о числе, отнесены к курсу математики 5–6 классов (введение дробных и отрицательных чисел). Однако нет другого раздела школьного курса математики, который усваивался бы с таким трудом, как раздел, посвященный переходу от множества рациональных чисел к множеству действительных чисел. Обойтись без иррациональных чисел в курсе элементарной математики нельзя, но ни одна из существующих теорий действительных чисел по своей сложности не может быть полностью изучена в средней школе.[10] Это связано с методическими трудностями, такими как:
· трудность актуализации рассматриваемых понятий;
· необходимость привлечения понятий, выходящих за рамки школьной программы;
· статичность исследуемой ситуации.
Говоря о существующих теориях действительных чисел, скажем, что в истории математики существует три способа определения понятия действительного числа: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте − теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда.[9] Как мы уже сказали, в школьном курсе математики данные способы как таковые не реализуются.
2.2. Методические рекомендации к реализации концепции дифференциации при обучении действительным числам
Современная математика должна быть важным источником знаний об окружающем мире, основой научно-технического прогресса, экономического прогресса, вместе с тем - одним из важнейших компонентов человеческой культуры. Математика, как предмет обучения естественного цикла, предназначенная формировать мировоззрение и компетентности, в которых нуждается современная жизнь.
По С. Ракову, под понятием «математическая компетентность» понимают способность личности видеть и применять математику в реальной жизни, понимать содержание и методы математического моделирования, строить математическую модель, исследовать ее методами математики, интерпретировать полученные результаты, оценивать погрешность вычислений. Урок в новом понимании это и средство развития личностных качеств ученика и обогащения его субъективного опыта, и среда для полноценной реализации учебных целей учеников. Урок следует рассматривать как средство развития личностных качеств ученика [13]. В частности таких как:
Ø инициативность;
Ø ответственность (готовность и способность обосновать основания собственного решения, прогнозировать последствия действий, нести ответственность за последствия);
Ø усердие и аккуратность в работе;
Ø производительность;
Ø мобильность;
Ø готовность к увеличенным нагрузкам;
Ø опыт группового решения проблем;
Ø умение планировать и прогнозировать;
Ø умение работать с информацией для себя и для группы;
Ø умение эффективно презентовать результаты работы;
Ø способность к рациональным, аргументированных, рефлексивных решений.
В процессе реализации дифференциальной модели обучения возникла проблема: как, имея в классе до 30 учащихся с различными возможностями, уровнем знаний, желанию, учитывая потребности каждого ученика, помочь ему не только получить соответствующие математические знания, но и стать компетентной личностью?
Пути решения этой проблемы нужно искать, опираясь на собственный опыт и изучая методические наработки современной педагогики. Современные требования обеспечить фундаментализацией образования на основе единства ее естественно-научной и гуманитарной составляющих, вооружение учащихся целостными знаниями и формирования в их сознании целостной картины мира, по мнению ученых и методистов связанные с задачами дифференциации обучения по всем базовым предметам и математики в частности. Во всем мире специалисты пришли к выводу, что невозможно обучать и научить всех учащихся на одинаковом уровне требований и объема знаний.
В проекции на школьное математическое образование требование «знать немного обо всем» должно обеспечиваться государственными стандартами, а тем, кто учится на повышенном и углубленном уровнях - должно предоставляться возможность узнать больше. Именно стандарт выделяет минимум содержания математического образования и минимальные требования к этому содержанию и становится основой дифференциации обучения. Уровневая дифференциация обязывает на основе безусловного достижения всеми учащимися минимального необходимого объема знаний и умений создать условия для повышенного и углубленного уровня обучения тех учеников, которые имеют к этому желание и возможности.
Учитывая все, что сказано выше, было решено в своей работе исследовать уровневую дифференциацию. Методическая литература предлагает разбивать класс на четыре группы:
1. Ученики с высоким темпом движения в обучении;
2. Ученики со средним темпом движения в обучении;
3. Ученики с низким темпом движения в обучении, имеющие трудности при изучении математики;
4. Неуспевающие ученики, которые значительно отстают в умственном развитии от сверстников и имеют существенные пробелы в знаниях.
Согласно мнению большинства, результаты дифференциального обучения могут быть более плодотворными и лучше, если работа в группах начинать с 5˗9 класса. Для работы мы выбрали 8 класс, так как в 8 классе дети начинают изучать действительные числа вплотную. Поэтому в 8 классе в начале учебного года, определив уровень знаний учеников, можно создать две группы: A и B. В группу А входят учащиеся 3-й и 4-й методических групп. В группу B попадают ученики 1-й и 2-й методических групп. Целесообразно будет создать именно две группы, потому что в условиях урока управления двумя группами более эффективно, чем четырьмя. Создание двух, а не четырех групп обусловлено еще и тем, что современные учебники учитывают наличие двух аналогичных групп, которое обеспечивает более качественное использование современных учебников и дидактической литературы при применении разноуровневого обучения на уроках.
Придя в 8 класс, учащиеся сначала делятся на группы по собственному желанию и выбору. Необходимо проинформировать детей, что задача группы A простые, а группы B сложные, так что в группе B работать труднее, но и результаты (достижения) в работе (учебе) будут лучше. Тот, кто выполняет задания группы B, сможет самостоятельно выполнить сложные задачи на проверочных работах. А значит, и получить высокую оценку.
Тем самым закладываются основы для определения цели работы (учебы) самим учеником, выбора методов достижения этой цели и положительной самооценки достигнутых результатов. То есть закладываются краеугольные камни компетентностного подхода к обучению. В начале обучения весь класс на уроках работает над задачами обоих групп совместно. Трудные задачи решаются коллективно, с полным объяснением решения. Ученики группы A при такой методике самостоятельно решают некоторые элементы тяжелых задач, могут в целом разобраться в решении достаточно сложных задач. Это, в общем, способствует повышению самооценки (часто несправедливо заниженной), вызывает интерес предметом и положительно влияет на результаты обучения.
Домашнее задание с самого начала задается каждой группе отдельно. В большинстве случаев оно состоит из четырех задач: первые две несложные, аналогичные тем, что решались в классе (как правило, это задача среднего уровня). Две другие - более сложные, выполняя их ученики должны подумать, догадаться, сопоставить ранее изученное с новым материалом. Четвертая задача, как правило, повышенной сложности.
Ученики знают, что если учитель проверяет домашнюю работу, полностью оценивая ее (ставит отдельную оценку за домашнее задание), то за верно выполнены первые две задачи они получат 3; за три 4, а за четыре - 5. При этом необходимо всячески поощрять «слабых» учеников, которые решают задачи группы B.
Ученик на определенных типах уроков, по своим возможностям и желанию может работать над задачами разных групп. Полностью в воле ученика направить усилия, использовать помощь учителя или родителей на улучшение своих достижений. Положительным считается и то, что ученик может сам решать и выбирать уровень обучения. Это приучает к самостоятельности, учит объективно оценивать свои возможности и достижения, формирует и воспитывает такие качества, как силу воли, целеустремленность, учит ставить перед собой цель и достигать ее, а, в общем, формирует личность как таковую.
Считается, что дифференцированный подход в этом смысле соответствует и основным современным направлениям образования - гуманизации и личностном подходе к процессу обучения. Ведь работая в своей группе. Ученик имеет возможность выполнить посильную задачу и получить определенное удовольствие, он самоутверждается - я это могу! Как следствие - у него не возникает отвращения к математике, как к чему-то тяжелому и непосильному, не объяснимому.
В дальнейшем на уроках разного типа или на разных этапах одного урока работу в дифференциальных группах организовывается по разному.
Если класс на группы не разделяется, то объяснение материала, доказательства теорем, или формул излагается всем ученикам на одинаковом уровне. При первичном закреплении более сложные задачи решают учащиеся группы B, проще - A.
Домашнее задание каждая группа получает разное:
1) группа A - знать формулы, формулировать определения, уметь применять при решении задач;
2) группа B - кроме задач группы A должна уметь выводить формулы и решать примеры более сложного уровня.
Есть уроки усвоения новых знаний, на которых класс делиться на группы, в которые входят ученики разные по способностям и достижениям. Задача такого урока:
- создать условия для развития способностей учащихся (как группы B, так и A);
- привлечь к продуктивной работе на уроке всех учеников;
- развивать коммуникативную компетентность учащихся;
- повысить заинтересованность учащихся к изучению как определенного материала, так и математики вообще.
На уроках формирования навыков и умений, как правило, группы получают разные задачи. Работу организовывается так:
Группа B. Получает задание соответствующей сложности. Каждый ученик группы решает эти задачи самостоятельно на своем рабочем месте. Одновременно два ученика этой группы выполняют задания у доски с целью дальнейшей проверки. Периодически (по мере решения задач) ученики сверяются с выполненными заданиями, исправляют ошибки, при необходимости получают консультацию учителя;
Группа A. Учащиеся группы под руководством учителя коллективно решают опорные упражнения и задачи темы на доске с полным объяснением. В конце такой работы они получают задания для самостоятельной учебной работы. По окончании работы в дифференциальных группах подводятся итоги, оценивается работа тех учеников, которые достигли хороших результатов.
Проиллюстрирую приведенную методику на фрагменте урока.
Контрольная работа.
Все ученики получают задание двух уровней, на их решение тратят разное количество времени: учащийся группы A медленно развязывает посильные задачи; учащийся группы B быстро развязывает простые задачи и переходит к более сложным. Таким образом, каждый может в полной мере реализовать свои возможности и продемонстрировать свои достижения в данной теме.
Ученые утверждают: природа компетенций такова, что она может проявляться только в органическом единстве с ценностями человека, то есть в условиях глубокой личной заинтересованности в данном виде деятельности [14].
Задания I уровня (группа A )
Понятие о действительном числе
1. Какое из чисел 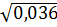 ,
, 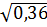 ,
, 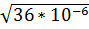 ,
, 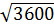 , является иррациональным [15]?
, является иррациональным [15]?
1) 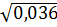 2)
2) 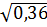 3)
3) 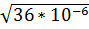 4)
4) 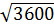
2. Какое из чисел 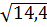 ,
, 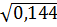 ,
, 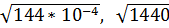 является рациональным [15]?
является рациональным [15]?
1) 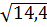 2)
2) 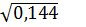 3)
3) 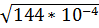 4)
4) 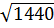
3. Среди чисел 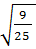 ,
, 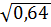 ,
, 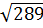 ,
, 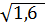 ,
, 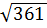 ,
, 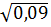 ,
, 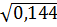 найдите иррациональное [15].
найдите иррациональное [15].
1) 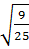 2)
2) 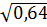 3)
3) 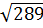 4)
4) 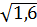 5)
5) 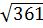
6) 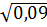 7)
7) 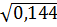 8) все числа рациональны.
8) все числа рациональны.
4. Укажите рациональное число среди данных 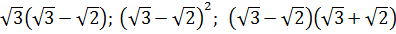 [15].
[15].
1) 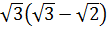 3)
3) 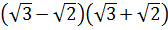
2) 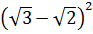 4) нет рационального числа
4) нет рационального числа
5. Укажите рациональное число среди данных 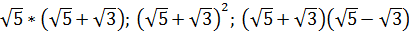 [15].
[15].
1) 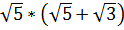 2
2 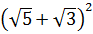
3) 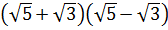 4) нет рационального числа
4) нет рационального числа
Ответы:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 4.7 | 3 | 2 |
Сравнение действительных чисел
1. Расположите в порядке возрастания числа 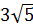 ;
; 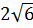 и 6 [16].
и 6 [16].
Ответ: ___________ .
2. Расположите числа 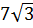 ;
; 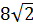 ;
; 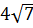 ;
; 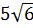 в порядке убывания [16].
в порядке убывания [16].
Ответ: ___________ .
3. Найдите сумму целых чисел, между которыми заключено число 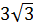 [16].
[16].
1) 23 2) 17 3) 19 4) 11
4. Какому промежутку принадлежит число 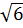 [16]?
[16]?
1) 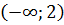 2)
2) 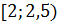 3)
3) 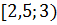 4) [
4) [ 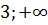 )
)
Ответы:
| 1 | 2 | 3 | 4 |
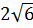 , 6, , 6, 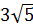
| 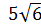 , , 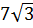 , , 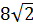 , , 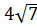
| 4 | 2 |
Понятие квадратного корня из неотрицательного числа
1. Найдите значение выражения 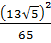 [15].
[15].
Ответ: ______ .
2. Вычислите:
1) 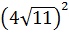 ; 2)
; 2) 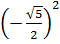 ; 3)
; 3) 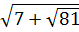 ; 4)
; 4) 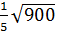 [15].
[15].
Ответы:
| 1 | 2 | |||
| 13 | 176 | 1,25 | 4 | 6 |
Свойства квадратных корней
1. Найдите значение выражения 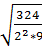 [15].
[15].
Ответ: ______ .
2. Найдите значение выражения 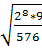 [15].
[15].
Ответ: ______ .
3. Вычислите 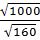 [15].
[15].
Ответ: ______ .
4. Вычислите 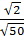 [15].
[15].
Ответ: ______ .
5. Найдите значение выражения 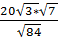 [15].
[15].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 | 4 | 5 |
| 3 | 2 | 2,5 | 0,2 | 10 |
Преобразование выражений, содержащих операцию извлечения квадратного корня
1. Внесите множитель под знак корня 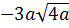 [16].
[16].
2. Внесите множитель под знак корня 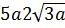 [16].
[16].
3. Вынесите множитель из-под знака корня 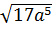 [16].
[16].
4. Вынесите множитель из-под знака корня 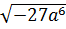 [16].
[16].
5. Упростите выражение 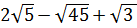 [16].
[16].
6. Упростите выражение 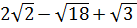 [16].
[16].
7. Упростите выражение 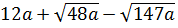 [16].
[16].
8. Упростите выражение 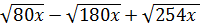 [16].
[16].
9. Найдите значение выражения 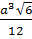 при
при 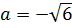 [16].
[16].
10. Найдите значение выражения 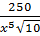 при
при 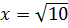 [16].
[16].
11. Вычислите 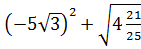 [16].
[16].
12. Вычислите 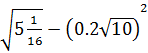 [16].
[16].
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 |
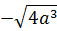
| 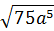
| 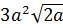
| 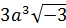
| 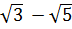
| 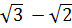
|
| 7 | 8 | 9 | 10 | 11 | 12 |
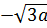
| 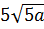
| -3 | 0.25 | 77.2 | 1.85 |
Задания II уровня (группа B )
Преобразование выражений, содержащих операцию извлечения квадратного корня
1. Найдите значение выражения 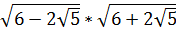 [17].
[17].
Ответ: ______ .
2. Найдите значение выражения 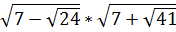 [17].
[17].
Ответ: ______ .
3. Вычислите 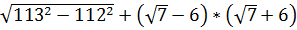 [17].
[17].
Ответ: ______ .
4. Вычислите 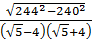 [17].
[17].
Ответ: ______ .
5. Сравните значения выражений 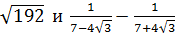 [17].
[17].
Ответ: ______ .
6. Сравните значения выражений 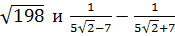 [17].
[17].
Ответ: ______ .
7. Упростите числовое выражение 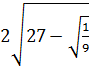 [17].
[17].
Ответ: ______ .
8. Упростите числовое выражение 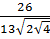 [18].
[18].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 5 | -14 | -4 | равно | больше | 6 | 1 |
Формула 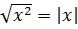
1. Найдите значение выражения 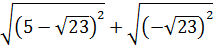 [17].
[17].
Ответ: ______ .
2. Найдите значение выражения 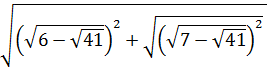 [17].
[17].
Ответ: ______ .
3. Найдите значение выражения 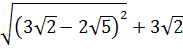 [17].
[17].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 |
| 1 | 1 | 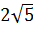
|
Дата: 2019-04-22, просмотров: 566.