Кафедра «Геометрии и методики преподавания математики»
«К защите»
И.о. зав. каф. геометрии и МПМ
________________/Исаева М.А./
«___» ______________ 2018г.
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
(квалификация – бакалавр)
Тема: «Методика преподования темы «действительные числа» в условиях уровневой дифференциации обучения»
| Выполнил: студент 5 курса, направления 44.03.05 – Педагогическое образование (профили подготовки «Математика» и «Информатика») очной формы обучения | _______________ | /Тимирбулатова М.М../ |
| Руководитель ВКР: доцент | _______________ | /Манаева Д,Х,/ |
| Консультанты: | ||
| 1. Аналитическая часть | _______________ | /Манаева Д,Х,/ |
| 2. Практическая часть | _______________ | /Манаева Д,Х,/ |
| Нормоконтроль, нач. УМУ | _______________ | /Хатаева Р.С./ |
| ВКР защищена на оценку ______________ (протокол № ___ «___» ___________ 2018 г.) | ||
Грозный, 2018
Содержание
Введение
Глава 1. Психолого-педагогические основы дифференциации обучения в школе
1.1. Сущность понятия дифференциация
1.2. Возможности и пути использования дифференциации в учебном процессе
Глава 2. Преподавание темы «Действительные числа» в условиях уровневой дифференциации обучения
2.1. Роль и место темы «Действительные числа» в систематическом курсе математики
2.2. Методические рекомендации к реализации концепции дифференциации при обучении действительным числам
2.3. Результаты экспериментальной проверки
2.4. Система упражнений для подготовки к ОГЭ учащихся девятых классов по теме «Действительные числа»
Заключение
Приложения
Литература
ВВЕДЕНИЕ
Актуальность работы. Под влиянием возрастающих требований жизни увеличивается объем и усложняется содержание знаний, подлежащих усвоению в школе. Но при традиционной системе обучения не каждый школьник способен освоить программу. По своим природным способностям, темпу работы и т.д. учащиеся сильно отличаются друг от друга. Нередко в одном классе можно наблюдать школьников как с очень высоким, так и с очень низким уровнем развития. Учитель обычно выбирает методы и формы обучения, ориентированные на среднего ученика. При этом слабым и сильным ученикам уделяется мало внимания. В этих условиях учащиеся с хорошими способностями работают без особого напряжения, а слабые учащиеся испытывают возрастающие затруднения.
В обучении математике эта проблема занимает особое место, что объясняется спецификой этого учебного предмета. Математика является одной из самых сложных школьных дисциплин и вызывает трудности у многих школьников.
Как показали многочисленные психолого-педагогические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех учащихся, положительное отношение их к уроку, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены по-разному. Одни школьники достаточно полно усвоят новое и могут применить его в новых, но сходных с учебной обстановкой условиях, требующих самостоятельного развития новых знаний (высший уровень усвоения).
Другие усвоят существенные стороны нового понятия или закономерности и сумеют применить их к решению задач, близких к тем, которые разбирались в процессе объяснения нового материала (средний уровень усвоения). Наконец, будут и такие, кто вынес лишь отдельные, нередко несущественные стороны нового понятия или закономерности и не может применить их к решению даже простых задач (низший уровень усвоения). При этом потребуется различное количество упражнений и различная мера помощи со стороны учителя тем учащимся, которых предстоит довести до высшего уровня усвоения.
Следовательно, необходима такая организация учебного процесса, которая позволила бы учитывать различия между учащимися и создавать оптимальные условия для эффективной учебной деятельности всех школьников, то есть возникает необходимость перестройки содержания, методов, форм обучения, максимально учитывающая индивидуальные особенности учеников. И подходом, который учитывает эти особенности, является дифференциация.
Объектом исследования является процесс обучения математике в условиях уровневой дифференциации в школе.
Предметом исследования: методика преподавания темы «Действительные числа» в школьном курсе математики.
Цель дипломного исследования – теоретически обосновать и экспериментально проверить эффективность дифференциации в обучении математике.
Задачи:
1. Изучить литературу по данной теме.
2. Раскрыть сущность понятия дифференциация.
3. Рассмотреть виды и типы дифференциации, возможности и пути использования дифференциации в учебном процессе.
4. Рассмотреть роль и место темы «Действительные числа» в систематическом курсе математики.
5. Представить методические подходы к реализации концепции дифференциации при обучении действительным числам.
6. Провести экспериментальное исследование и проанализировать результаты.
7. Составить систему упражнений для подготовки к ОГЭ учащихся девятых классов по теме «Действительные числа».
Дипломная работа состоит из введения, двух глав, заключения, приложения и списка литературы.
Во введении сформулированы основные характеристики исследования: актуальность, объект, предмет, цель и задачи.
Глава I посвящена психолого-педагогическим основам дифференциации обучения в школе. В данной главе даны основные определения по теме исследования, представлены исторические аспекты возникновения и развития идеи дифференциации, рассмотрены виды дифференциации.
Во II главе представлены роль и место темы «Действительные числа» в систематическом курсе математики, рассмотрены методические рекомендации к реализации концепции дифференциации при обучении действительным числам. Представлена экспериментальная работа и система упражнений для подготовки к ОГЭ учащихся 9-ых классов по теме «Действительные числа».
В заключении сформулированы основные результаты и выводы проведённого исследования.
Список литературы содержит … наименования.
Задания I уровня (группа A )
Понятие о действительном числе
1. Какое из чисел 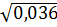 ,
, 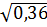 ,
, 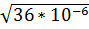 ,
, 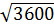 , является иррациональным [15]?
, является иррациональным [15]?
1) 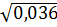 2)
2) 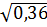 3)
3) 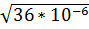 4)
4) 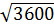
2. Какое из чисел 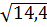 ,
, 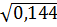 ,
, 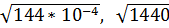 является рациональным [15]?
является рациональным [15]?
1) 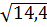 2)
2) 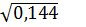 3)
3) 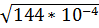 4)
4) 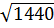
3. Среди чисел 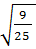 ,
, 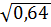 ,
, 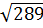 ,
, 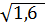 ,
, 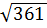 ,
, 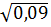 ,
, 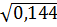 найдите иррациональное [15].
найдите иррациональное [15].
1) 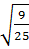 2)
2) 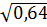 3)
3) 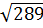 4)
4) 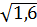 5)
5) 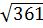
6) 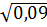 7)
7) 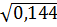 8) все числа рациональны.
8) все числа рациональны.
4. Укажите рациональное число среди данных 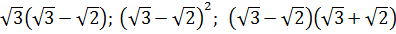 [15].
[15].
1) 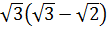 3)
3) 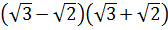
2) 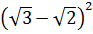 4) нет рационального числа
4) нет рационального числа
5. Укажите рациональное число среди данных 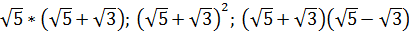 [15].
[15].
1) 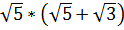 2
2 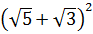
3) 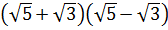 4) нет рационального числа
4) нет рационального числа
Ответы:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 4.7 | 3 | 2 |
Сравнение действительных чисел
1. Расположите в порядке возрастания числа 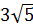 ;
; 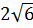 и 6 [16].
и 6 [16].
Ответ: ___________ .
2. Расположите числа 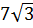 ;
; 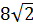 ;
; 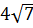 ;
; 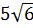 в порядке убывания [16].
в порядке убывания [16].
Ответ: ___________ .
3. Найдите сумму целых чисел, между которыми заключено число 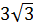 [16].
[16].
1) 23 2) 17 3) 19 4) 11
4. Какому промежутку принадлежит число 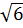 [16]?
[16]?
1) 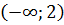 2)
2) 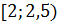 3)
3) 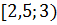 4) [
4) [ 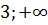 )
)
Ответы:
| 1 | 2 | 3 | 4 |
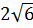 , 6, , 6, 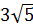
| 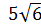 , , 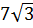 , , 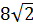 , , 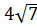
| 4 | 2 |
Понятие квадратного корня из неотрицательного числа
1. Найдите значение выражения 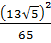 [15].
[15].
Ответ: ______ .
2. Вычислите:
1) 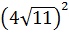 ; 2)
; 2) 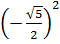 ; 3)
; 3) 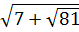 ; 4)
; 4) 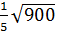 [15].
[15].
Ответы:
| 1 | 2 | |||
| 13 | 176 | 1,25 | 4 | 6 |
Свойства квадратных корней
1. Найдите значение выражения 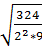 [15].
[15].
Ответ: ______ .
2. Найдите значение выражения 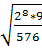 [15].
[15].
Ответ: ______ .
3. Вычислите 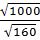 [15].
[15].
Ответ: ______ .
4. Вычислите 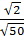 [15].
[15].
Ответ: ______ .
5. Найдите значение выражения 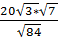 [15].
[15].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 | 4 | 5 |
| 3 | 2 | 2,5 | 0,2 | 10 |
Преобразование выражений, содержащих операцию извлечения квадратного корня
1. Внесите множитель под знак корня 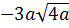 [16].
[16].
2. Внесите множитель под знак корня 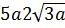 [16].
[16].
3. Вынесите множитель из-под знака корня 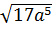 [16].
[16].
4. Вынесите множитель из-под знака корня 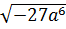 [16].
[16].
5. Упростите выражение 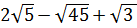 [16].
[16].
6. Упростите выражение 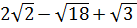 [16].
[16].
7. Упростите выражение 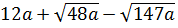 [16].
[16].
8. Упростите выражение 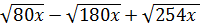 [16].
[16].
9. Найдите значение выражения 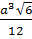 при
при 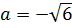 [16].
[16].
10. Найдите значение выражения 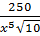 при
при 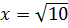 [16].
[16].
11. Вычислите 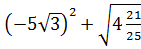 [16].
[16].
12. Вычислите 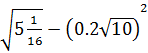 [16].
[16].
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 |
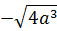
| 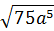
| 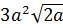
| 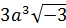
| 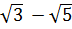
| 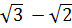
|
| 7 | 8 | 9 | 10 | 11 | 12 |
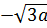
| 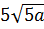
| -3 | 0.25 | 77.2 | 1.85 |
Задания II уровня (группа B )
Преобразование выражений, содержащих операцию извлечения квадратного корня
1. Найдите значение выражения 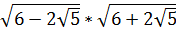 [17].
[17].
Ответ: ______ .
2. Найдите значение выражения 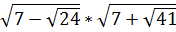 [17].
[17].
Ответ: ______ .
3. Вычислите 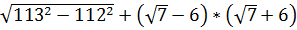 [17].
[17].
Ответ: ______ .
4. Вычислите 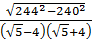 [17].
[17].
Ответ: ______ .
5. Сравните значения выражений 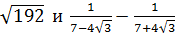 [17].
[17].
Ответ: ______ .
6. Сравните значения выражений 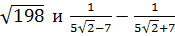 [17].
[17].
Ответ: ______ .
7. Упростите числовое выражение 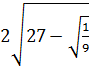 [17].
[17].
Ответ: ______ .
8. Упростите числовое выражение 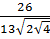 [18].
[18].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 5 | -14 | -4 | равно | больше | 6 | 1 |
Формула 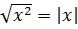
1. Найдите значение выражения 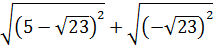 [17].
[17].
Ответ: ______ .
2. Найдите значение выражения 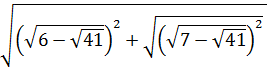 [17].
[17].
Ответ: ______ .
3. Найдите значение выражения 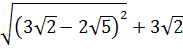 [17].
[17].
Ответ: ______ .
Ответы:
| 1 | 2 | 3 |
| 1 | 1 | 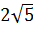
|
Числа и вычисления
Пример 1. Сколько целых чисел расположено между числами 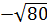 и
и 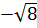 [19]?
[19]?
Решение:
1) 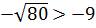
2) 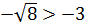
3) тогда получаем: 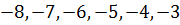
Ответ: 6.
Пример 2. Какое из чисел отмечено на координатной прямой точкой 𝐴 [19]?
A x
0 1 2 3 4
1) 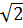 ; 2)
; 2) 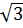 ; 2)
; 2) 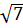 ; 2)
; 2) 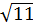 .
.
Решение: Возведем в квадрат числа 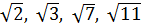 :
:
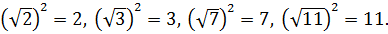
Число 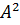 лежит между числами
лежит между числами 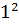 = 1 и
= 1 и 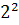 = 4 и ближе к числу
= 4 и ближе к числу 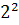 . Поэтому точкой A отмечено число
. Поэтому точкой A отмечено число 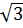 .
.
Ответ: 2.
Пример 3. Одна из точек, отмеченных на координатной прямой, соответствует числу 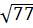 . Какая это точка [19]?
. Какая это точка [19]?
A B C D x
7 8 9
1) точка A; 2) точка B; 3) точка C; 4) точка D.
Решение:
Возведем в квадрат числа 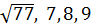 :
:
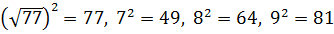 .
.
Число 77 лежит между числами 64 и 81 и находится ближе к числу 81, поэтому 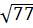 соответствует точке D.
соответствует точке D.
Ответ: 4.
Задания:
1. Сколько целых чисел расположено между числами 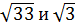 ?
?
2. Сколько целых чисел расположено между числами 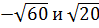 ?
?
3. Сколько целых чисел расположено между числами 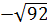 и
и 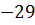 ?
?
4. Сколько целых чисел расположено между числами 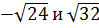 ?
?
5. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 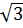 ; 2)
; 2) 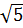 ; 3)
; 3) 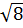 ; 4)
; 4) 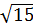 .
.
6. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 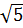 ; 2)
; 2) 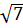 ; 3)
; 3) 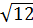 ; 4)
; 4) 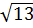 .
.
7. Какое из чисел отмечено на координатной прямой точкой A?
A x
0 1 2 3 4
1) 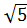 ; 2)
; 2) 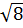 ; 3)
; 3) 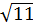 ; 4)
; 4) 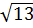 .
.
8. Одна из точек, отмеченных на координатной прямой, соответствует числу 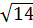 . Какая это точка?
. Какая это точка?
M N P Q x
3 4 5
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
9. Одна из точек, отмеченных на координатной прямой, соответствует числу 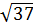 . Какая это точка?
. Какая это точка?
M N P Q x
5 6 7
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
10. Одна из точек, отмеченных на координатной прямой, соответствует числу 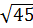 . Какая это точка?
. Какая это точка?
M N P Q
6 7 8
1) точка M; 2) точка N; 3) точка P; 4) точка Q.
Алгебраические выражения
Пример 1. Укажите наибольшее из следующих чисел [19]:
1) 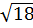 ; 2)
; 2) 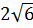 ; 3) 5; 4)
; 3) 5; 4) 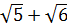 .
.
Решение: Возведем в квадрат числа 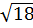 ;
; 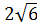 ; 5;
; 5; 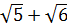 :
:
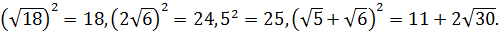
Поскольку 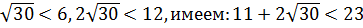 .
.
Таким образом, наибольшее число 5.
Ответ: 3.
Пример 2. Расположите в порядке возрастания числа 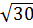 ;
; 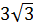 ; 5,5 [19].
; 5,5 [19].
1) 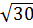 ;
; 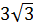 ; 5,5; 2) 5,5;
; 5,5; 2) 5,5; 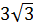 ;
; 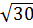 ; 3)
; 3) 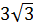 ; 5,5;
; 5,5; 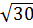 ; 4)
; 4) 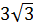 ;
; 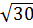 ; 5,5.
; 5,5.
Решение: Возведем каждое из чисел в квадрат:
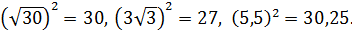
Сравним квадраты заданных чисел: 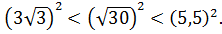
Следовательно, 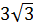 ;
; 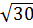 ; 5,5.
; 5,5.
Ответ: 4.
Пример 3. Найдите значение выражения 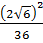 [19].
[19].
1)  ; 2)
; 2)  ; 3) 2; 4) 4.
; 3) 2; 4) 4.
Решение: Последовательно получаем:
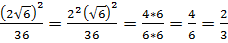 .
.
Ответ: 1.
Задания:
1. Укажите наибольшее из следующих чисел:
1) 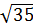 ; 2)
; 2) 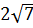 ; 3) 6; 4)
; 3) 6; 4) 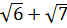 .
.
2. Укажите наименьшее из следующих чисел:
1) 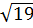 ; 2)
; 2) 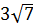 ; 3) 6; 4)
; 3) 6; 4) 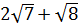 .
.
3. Укажите наибольшее из следующих чисел:
1) 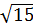 ; 2)
; 2) 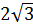 ; 3) 3; 4)
; 3) 3; 4) 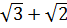 .
.
4. Укажите наименьшее из следующих чисел:
1) 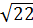 ; 2)
; 2) 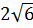 ; 3)
; 3) 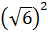 ; 4)
; 4) 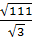 .
.
5. Расположите в порядке возрастания числа 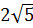 ;
; 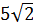 ; 6.
; 6.
1) 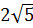 ;
; 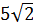 ; 6; 2)
; 6; 2) 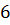 ;
; 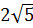 ;
; 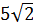 ; 3)
; 3) 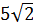 ; 6;
; 6; 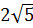 ; 4)
; 4) 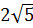 ; 6;
; 6; 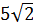 .
.
6. Расположите в порядке возрастания числа 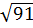 ; 9,5;
; 9,5; 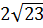 .
.
1) 9,5; 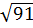 ;
; 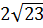 ; 2)
; 2) 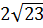 ;
; 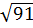 ; 9,5; 3) 9,5;
; 9,5; 3) 9,5; 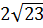 ;
; 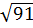 ; 4)
; 4) 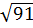 ; 9,5;
; 9,5; 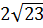 .
.
7. Расположите в порядке возрастания числа 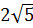 ;
; 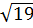 ; 4,5.
; 4,5.
1) 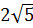 ;
; 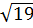 ; 4,5; 2)
; 4,5; 2) 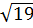 ; 4,5;
; 4,5; 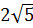 ; 3)
; 3) 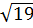 ;
; 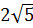 ; 4,5; 4) 4,5;
; 4,5; 4) 4,5; 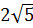 ;
; 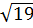 .
.
8. Расположите в порядке возрастания числа 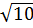 ;
; 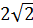 ; 3,5.
; 3,5.
1) 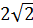 ; 3,5;
; 3,5; 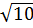 ; 2) 3,5;
; 2) 3,5; 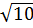 ;
; 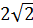 ; 3)
; 3) 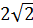 ;
; 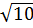 ; 3,5; 4)
; 3,5; 4) 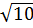 ;
; 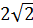 ; 3,5.
; 3,5.
9. Найдите значение выражения  .
.
1)  ; 2) 3; 3)
; 2) 3; 3)  ; 4)
; 4)  .
.
10. Найдите значение выражения 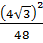 .
.
1)  ; 2) 27; 3)
; 2) 27; 3) 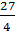 ; 4) 1.
; 4) 1.
11) Найдите значение выражения 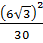 .
.
1)  ; 2)
; 2) 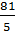 ; 3)
; 3) 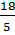 ; 4)
; 4) 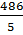 .
.
12. Найдите значение выражения 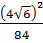 .
.
1) 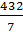 ; 2)
; 2)  ; 3)
; 3) 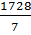 ; 4)
; 4)  .
.
ПРИЛОЖЕНИЯ
1.2.3.4.
ЗАКЛЮЧЕНИЕ
Успех проводимой в нашей стране модернизации образования во многом зависит от правильного определения роли и места каждого школьного предмета в новых, быстро меняющихся условиях. При этом определены приоритетные направления развития школы, такие как гуманизация, гуманитаризация, ориентированные на формирование личности школьников, реализацию их задатков, склонностей, способностей, интересов и других индивидуальных особенностей. В этом большую роль играет школьный курс математики.
Современная тенденция в раскрытии сущности дифференциации обучения состоит в том, что дифференциацию обучения понимают как систему, которая лежит в основе учебно-воспитательного процесса (то есть является организационно-методическим принципом построения школы) и направлена на реализацию индивидуального подхода в обучении.
Внедрение в практику учебно-воспитательной работы принципа индивидуального подхода требует разработки системы воздействия на ученика с учетом его индивидуальных и возрастных возможностей, то есть внедрение дифференциации обучения.
Опыт внедрения дифференциального метода для преподавания темы «Действительные числа» показал свою эффективность, улучшено усвоение знаний, о чем свидетельствует повышение успеваемости класса.
ЛИТЕРАТУРА
1. Сухомлинский В.А. Избранные произведения: в 5 т. – Киев: Радянська школа, 1979, т1.
2. Унт И.Э. Индивидуализация и дифференциация обучения.- М.:Педагогика,1990.
3. Чередов И.М. Формы учебной работы в средней школе.- М.: Просвещение,1988.
4. Рабунский Е.С. Индивидуальный подход в процессе обучения школьников.- М.: Педагогика, 1975.
5. Чередов И.М. О дифференцированном обучении на уроках.- М.: Просвещение,1973.
6. Блонский П.П. о фуркации на втором концентре школы второй ступени
7. Андронов, И.К. Математика действительных и комплексных чисел [Текст]/ И.К.Андронов. – М.: Просвещение, 1975. – 158 с. Блок А.Я. Методика преподавания математики в средней школе: Частная методика: Учебное пособие для студентов пед. институтов по физ-мат спец. / А.Я. Блок, В.А. Гусев, Г.В. Дорофеев [и др.]; сост. В.И. Мишин. – М: Просвеще- ние, 1987
8. Александров, А.Д. Математика, ее содержание, методы и значение [Текст]/ Под ред. Александрова А.Д., Колмогорова А.Н., Лаврентьева М.А. – М.: Изд. Академии наук СССР, 2016.
9. Методика и технология обучения математике. Курс лекций: пособие для вузов[Текст]/ Под ред. Н.Л. Стефановой, Н.С. Подходовой. – М.: Дрофа, 2015.
10. Столяр, А.А. Логические проблемы преподавания математики [Текст]/ А.А. Столяр. – Минск: Высшая школа, 2015.
11. Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. - М .: Просвещение, 2016.
12. Аргунов Б.И., Балк М.Б. Элементарная геометрия. – М.: Просвещение, 2016.
13. Алфутова, А.Б. Алгебра и теория чисел для математических школ [Текст]/ А.Б. Алфутова, А.В. Устинов. – М.: МЦНМО, 2013.
14. Ключникова Е.М., Рабочая тетрадь по алгебре. 8 класс. К учебнику А.Г. Мордковича [Текст] / Е.М. Ключникова, И.В. Комиссарова. – М: Мнемозина, 2013.
15. Задачи по математике: алгебра и начала анализа [Текст]/ М.И. Башмаков, Б.М. Беккер, В.М. Гольховой. – М.: Высшая школа, 2004.
16. Байдак В.А. Теория и методика обучения математики: Учебное пособие [Текст] / В.А. Байдак. – М.: Флинта, 2011.
17. ОГЭ. 3000 задач с ответами по математике. Все задания части 1. Под. ред. Ященко И.В. М.: 2015.
Кафедра «Геометрии и методики преподавания математики»
«К защите»
И.о. зав. каф. геометрии и МПМ
________________/Исаева М.А./
«___» ______________ 2018г.
Дата: 2019-04-22, просмотров: 576.